Tea

Tea
Tea
Creator	David Wheeler and Roger Needham
Created by	1994
Published	1994
Key size	128 bit
Block size	64 bit
Number of rounds	64 (32 cycles)
Type of	Feistel Network

In cryptography , the Tiny Encryption Algorithm (TEA) ^[1] is a block encryption algorithm of the Feistel Network type. The algorithm was developed at the Department of Computer Science at the University of Cambridge David Wheeler and Roger Needham and was first presented in 1994 ^[2] at the Symposium on Fast Encryption Algorithms in Leuven ( Belgium ).

The cipher is not patented , it is widely used in a number of cryptographic applications and a wide range of hardware due to extremely low memory requirements and ease of implementation. The algorithm has both a software implementation in different programming languages and a hardware implementation on integrated circuits such as FPGA .

Content

1 Properties
2 Description of the algorithm
3 Implementation
4 Cryptanalysis
- 4.1 Attacks on related keys
- 4.2 Differential cryptanalysis
- 4.3 Equivalent keys
5 Algorithm Extensions
- 5.1 XTEA
- 5.2 XXTEA
- 5.3 RTEA
- 5.4 Raiden
- 5.5 Comparison of different versions of the extension of the TEA algorithm
6 See also
7 notes
8 References

Properties

The TEA encryption algorithm ^{[1] is} based on bit operations with a 64-bit block and has a 128-bit encryption key . The standard number of Feistel network rounds is 64 (32 cycles), however, to achieve the best performance or encryption, the number of cycles can be varied from 8 (16 rounds) to 64 (128 rounds). The Feistel network is asymmetric due to the use of modulo 2 ³² addition as an operation of superposition.

The advantages of a cipher are its simplicity in implementation, small code size and rather high speed of execution, as well as the ability to optimize execution on standard 32-bit processors, as the main operations are XOR , bitwise shift and addition operations module 2 ³² . Since the algorithm does not use lookup tables and the round function is quite simple, the algorithm requires at least 16 cycles (32 rounds) to achieve effective diffusion, although complete diffusion is already achieved in 6 cycles (12 rounds). ^[one]

The algorithm has excellent resistance to linear cryptanalysis and quite good to differential cryptanalysis . The main drawback of this encryption algorithm is its vulnerability to “related -key attack ” attacks. Due to the simple key schedule, each key has 3 equivalent keys. This means that the effective key length is only 126 bits ^[3] ^[4] , so this algorithm should not be used as a hash function .

Algorithm Description

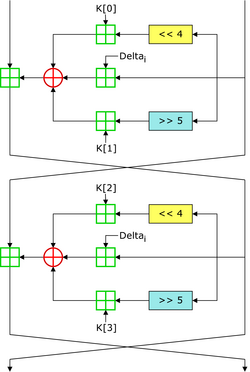
The source text is broken into blocks of 64 bits each. The 128-bit key K is divided into four 32-bit subkeys K [0], K [1], K [2] and K [3]. This completes the preparatory process, after which each 64-bit block is encrypted for 32 cycles (64 rounds) according to the algorithm below. ^[5]

Suppose that the right and left parts (L _n , R _n ) arrive at the input of the nth round (for 1 ≤ n ≤ 64), then the left and right parts (L _{n + 1} , R _{n +1} ), which are calculated according to the following rules:

L _{n + 1} = R _n .

If n = 2 * i - 1 for 1 ≤ i ≤ 32 (odd rounds), then R _{n + 1} = L _n $\boxplus$ ${\ displaystyle \ boxplus}$ ({[R _n $\ll$ ${\ displaystyle \ ll}$ four ] $\boxplus$ ${\ displaystyle \ boxplus}$ K [0]} $\oplus$ ${\ displaystyle \ oplus}$ {R _n $\boxplus$ ${\ displaystyle \ boxplus}$ i * δ} $\oplus$ ${\ displaystyle \ oplus}$ {[R _n $\gg$ ${\ displaystyle \ gg}$ 5 ] $\boxplus$ ${\ displaystyle \ boxplus}$ K [1]})

If n = 2 * i for 1 ≤ i ≤ 32 (even rounds), then R _{n + 1} = L _n $\boxplus$ ${\ displaystyle \ boxplus}$ ({[R _n $\ll$ ${\ displaystyle \ ll}$ four ] $\boxplus$ ${\ displaystyle \ boxplus}$ K [2]} $\oplus$ ${\ displaystyle \ oplus}$ {R _n $\boxplus$ ${\ displaystyle \ boxplus}$ i * δ} $\oplus$ ${\ displaystyle \ oplus}$ {[R _n $\gg$ ${\ displaystyle \ gg}$ 5 ] $\boxplus$ ${\ displaystyle \ boxplus}$ K [3]})

Where

X $\boxplus$ ${\ displaystyle \ boxplus}$ Y is the operation of adding the numbers X and Y modulo 2 ³² .
X $\oplus$ ${\ displaystyle \ oplus}$ Y is the bitwise exclusive "OR" (XOR) of the numbers X and Y, which in the C programming language is denoted as X ^ Y
X $\ll$ ${\ displaystyle \ ll}$ Y and X $\gg$ ${\ displaystyle \ gg}$ Y - bitwise shift operations of the number X by Y bits left and right, respectively.
The constant δ was derived from the Golden Ratio δ = ( ${\sqrt {5}}$ ${\ displaystyle {\ sqrt {5}}}$ - 1) * 2 ³¹ = 2654435769 = 9E3779B9 _h ^[2] . In each round, the constant is multiplied by the cycle number i. This was done to prevent simple attacks based on the symmetry of the rounds.

It is also obvious that the TEA encryption algorithm does not, as such, have a key schedule algorithm. Instead, in odd rounds, use subkeys K [0] and K [1], in even ones - K [2] and K [3].

Since this is a block cipher algorithm, where the block length is 64-bit, and the data length may not be a multiple of 64-bits, the values of all bytes complementing the block up to a frequency of 64-bits are set to 0x01.

Implementation

Implementation in the C programming language (adapted version of the code presented in an article by David Wheeler and Roger Needham ^[2] ) of encryption and decryption functions using the TEA algorithm:

  #include <stdint.h> 

 void encrypt ( uint32_t * v , uint32_t * k )
 {
     / * set up * /
     uint32_t v0 = v [ 0 ];
     uint32_t v1 = v [ 1 ];
     uint32_t sum = 0 ;
     uint32_t i ;

     / * a key schedule constant * /
     uint32_t delta = 0x9e3779b9 ;

     / * cache key * /
     uint32_t k0 = k [ 0 ];
     uint32_t k1 = k [ 1 ];
     uint32_t k2 = k [ 2 ];
     uint32_t k3 = k [ 3 ];

     / * basic cycle start * /
     for ( i = 0 ; i < 32 ; i ++ )
     {
         sum + = delta ;
         v0 + = (( v1 << 4 ) + k0 ) ^ ( v1 + sum ) ^ (( v1 >> 5 ) + k1 );
         v1 + = (( v0 << 4 ) + k2 ) ^ ( v0 + sum ) ^ (( v0 >> 5 ) + k3 );
     }
     / * end cycle * /

     v [ 0 ] = v0 ;
     v [ 1 ] = v1 ;
 }

 void decrypt ( uint32_t * v , uint32_t * k )
 {
     / * set up * /
     uint32_t v0 = v [ 0 ];
     uint32_t v1 = v [ 1 ];
     uint32_t sum = 0xC6EF3720 ;
     uint32_t i ;

     / * a key schedule constant * /
     uint32_t delta = 0x9e3779b9 ;

     / * cache key * /
     uint32_t k0 = k [ 0 ];
     uint32_t k1 = k [ 1 ];
     uint32_t k2 = k [ 2 ];
     uint32_t k3 = k [ 3 ];        

     / * basic cycle start * /
     for ( i = 0 ; i < 32 ; i ++ )
     {                              
         v1 - = (( v0 << 4 ) + k2 ) ^ ( v0 + sum ) ^ (( v0 >> 5 ) + k3 );
         v0 - = (( v1 << 4 ) + k0 ) ^ ( v1 + sum ) ^ (( v1 >> 5 ) + k1 );
         sum - = delta ;                                   
     }
     / * end cycle * /

     v [ 0 ] = v0 ;
     v [ 1 ] = v1 ;
 }

Comments:

v - source text consisting of two parts of 32 bits
k - a key consisting of four 32-bit parts

Changes from the original code:

uint32_t is used because it always has a size of 32 bits, as opposed to long (present in the original code), which can contain 64 bits (for example, on some 64 bit systems)
source code does not use type const
in the source code, the excess brackets in the expressions for v0 and v1 are omitted, in this modification they are left for greater clarity

Cryptanalysis

It is assumed that this algorithm provides security comparable to the IDEA encryption algorithm, since it uses the same idea of using operations from orthogonal algebraic groups . ^[1] This approach perfectly protects against linear cryptanalysis methods.

Related Key Attacks

The algorithm is most vulnerable to “ related -key attack ” ( Eng. Related-key attack ), due to the simple schedule of keys (including the lack of a key schedule algorithm as such). There are at least three known attacks of this type, they were presented in the work of John Kelsea ( John Kelsea ), Bruce Schneier ( Bruce Schneier ) and David Wagner ( David Wagner ) in 1997 ^[6] . The simplest of them give a differential characteristic with a probability of ^2–32 after 32 cycles of the algorithm, therefore, at least 2 ³⁴ selected plaintexts are required to find a differential characteristic with probability 1 and determine all bits of the key. A more difficult attack to implement, combining the ideas of “attack on bound keys” by Eli Biham ^[7] and differential attack gives a differential characteristic with a probability of 2 ⁻¹¹ , requires only 2 ²³ selected plaintexts and a time of the order of 2 ³² times encryption (that is, it requires a number of bit operations of the order of 2 ³² ).

Differential Cryptanalysis

It was found that TEA is quite resistant to differential cryptanalysis . An attack on 10 rounds of TEA requires 2 ^52.5 selected plaintexts and has a time complexity of 2 ⁸⁴ ^[8] . The best result is cryptanalysis of 17 rounds of TEA ^[9] . This attack requires a total of 1920 selected plaintexts, but has a temporary difficulty of 2 ^123.37 .

Equivalent Keys

Another problem with the TEA algorithm is the presence of equivalent keys. It was shown that each key has three equivalent keys ^[4] . This means that the effective key length is only 126 bits instead of 128 intended by the developers, so TEA is undesirable to use as a hash function , which was reflected in Andrew Huang’s book “Hacking the Xbox: an introduction to reverse engineering” on An example of hacking a Microsoft Xbox game console.

Equivalent Key Table:

K [0]	K [1]	K [2]	K [3]
K [0]	K [1]	K [2] $\oplus$ ${\ displaystyle \ oplus}$ 80,000,000 _h	K [3] $\oplus$ ${\ displaystyle \ oplus}$ 80,000,000 _h
K [0] $\oplus$ ${\ displaystyle \ oplus}$ 80,000,000 _h	K [1] $\oplus$ ${\ displaystyle \ oplus}$ 80,000,000 _h	K [2]	K [3]
K [0] $\oplus$ ${\ displaystyle \ oplus}$ 80,000,000 _h	K [1] $\oplus$ ${\ displaystyle \ oplus}$ 80,000,000 _h	K [2] $\oplus$ ${\ displaystyle \ oplus}$ 80,000,000 _h	K [3] $\oplus$ ${\ displaystyle \ oplus}$ 80,000,000 _h

Algorithm Extensions

Identification of a number of serious vulnerabilities and weaknesses in the original TEA algorithm led to the rapid creation of its extensions. The main differences of all these algorithms are an improved key schedule, the dynamic dependence of the key on the text, as well as a different key size, input block and / or the number of rounds of the Feistel network.

XTEA

XTEA has a block size of 64 bits, a key size of 128 bits, the number of Feistel network rounds is 64. The algorithm was developed by David Wheeler and Roger Needham and published in 1997 . The main difference from the original TEA algorithm is the presence of a key schedule algorithm, which eliminated the critical vulnerability to “attacks on related keys”, but led to a deterioration in resistance to differential cryptanalysis ^[9] . There are three modifications of this algorithm developed by Tom Denis ^[10] : XTEA -1 (block size - 64 bits, key size - 128 bits, number of Feistel network rounds - 32), XTEA -2 (block size - 128 bits , the key size is 128 bits, the number of rounds of the Feistel network is 64) and XTEA -3 (the block size is 128 bits, the size of the key is 256 bits, the number of rounds of the Feistel network is 64).

XXTEA

In 1998, the following extension of the algorithm, called XXTEA , was published. The key size is 128 bits. A distinctive feature is the ability to encrypt any blocks that are a multiple of 64 bits, the number of rounds is 52 + 6 * (the number of 32-bit words in a block) or 52 + 12 * M with a block length of 64 * M bits. The practical effectiveness of an anonymous differential attack published has not been proven ^[11] .

RTEA

There is also an alternative modification of the TEA algorithm, called RTEA , developed in 2007 by Marcos el Ruptor . Block size - 64 bits; for a 128-bit key, the number of rounds of the Feistel network is 48, for 256-bit - 64. According to the developers, this algorithm is more efficient and more resistant to cryptanalysis ^[12] than XTEA, however, this algorithm already has an “attack on linked keys” ^[13] .

Raiden

Using genetic programming mechanisms, in 2006 a Raiden algorithm was created by a team of developers led by Julio César Hernández Castro to eliminate the vulnerabilities of the TEA cipher. It repeats almost exactly the structure of the TEA algorithm, except that the Raiden algorithm has an advanced key schedule algorithm. The standard number of Feistel network rounds is 32 (16 cycles). Raiden uses a key schedule close to the PRNG , transforms the key, and generates subkeys for each round. The cipher successfully passes the tests of Diehard , Sexton and ENT ^[14] .

Comparison of different versions of the TEA algorithm extension

Here is a comparative table of the main characteristics of the TEA family of algorithms:

Algorithm Name	The standard number of rounds of the Feistel network	Block size	Key size
Tea	64	64 bits	128 bit
XTEA	64	64 bits	128 bit
XTEA-1	32	64 bits	128 bit
XTEA-2	64	128 bit	128 bit
XTEA-3	64	128 bit	256 bit
XXTEA	52 + 12 * M	64 * M bit	128 bit
RTEA	48 or 64	64 bits	128 or 256 bit
Raiden	32	64 bits	128 bit

At the same time, the authors of the TEA algorithm on their official page ^[1] draw attention to the fact that in real conditions of practical use, the TEA algorithm is still quite reliable and all the vulnerabilities found are usually not critical, for example, during transmission real time data.

Notes

↑ ¹ ² ³ ⁴ ⁵ TEA cipher page
↑ ¹ ² ³ Roger M. Needham and David J. Wheeler. TEA, a Tiny Encryption Algorithm
↑ Kelsey, John; Schneier, Bruce; Wagner, David. Key-schedule cryptanalysis of IDEA, G-DES, GOST, SAFER, and Triple-DES (English) // Lecture Notes in Computer Science: journal. - 1996. - Vol. 1109 . - P. 237-251 . - DOI : 10.1007 / 3-540-68697-5_19 .
↑ ¹ ² Andem, Vikram Reddy (2003). A cryptoanalisys of the tiny encryption algorithm Archived on April 20, 2009.
↑ Seokhie Hong, Deukjo Hong, Youngdai Ko, Donghoon Chang, Wonil Lee, Sangjin Lee, (2003). Differential Cryptanalysis of TEA and XTEA
↑ Kelsey, John; Schneier, Bruce; Wagner, David. Related-key cryptanalysis of 3-WAY, Biham-DES, CAST, DES-X NewDES, RC2, and TEA (English) // Lecture Notes in Computer Science: journal. - 1997. - Vol. 1334 . - P. 233-246 . - DOI : 10.1007 / BFb0028479 .
↑ Eli Biham, Computer Science Department, Technion - Israel Institute of Technology, Haifa 32000, Israel, (1992). "New Types of Cryptanalytic Attacks Using Related Keys"
↑ Moon, Dukjae; Hwang, Kyungdeok; Lee, Wonil; Lee, Sangjin; Lim, Jongin. Impossible differential cryptanalysis of reduced round XTEA and TEA (English) // Lecture Notes in Computer Science: journal. - 2002. - Vol. 2365 . - P. 49-60 . - DOI : 10.1007 / 3-540-45661-9_4 .
↑ ¹ ² Hong, Seokhie; Hong, Deukjo; Ko, Youngdai; Chang, Donghoon; Lee, Wonil; Lee, Sangjin. Differential cryptanalysis of TEA and XTEA (neopr.) // In Proceedings of ICISC 2003 .-- 2003.
↑ Tom St Denis. Extended TEA Algorithms
↑ Original article with the implementation of the attack on XXTEA and an example code (unopened) (inaccessible link) Date of treatment November 6, 2009. Archived September 23, 2009.
↑ Comparative stability results of symmetric cryptographic algorithms Archived July 25, 2008. (eng.)
↑ A related key attack for RTEA. (inaccessible link)
↑ Raiden: An alternative to TEA Block Cipher

Links

TEA Encryption Algorithm Page
Roger M. Needham and David J. Wheeler. TEA, a Tiny Encryption Algorithm (PDF)
Andew Hang. "Hacking the Xbox: an introduction to reverse engineering" [1] ISBN 978-1593270292
Hacker Online Magazine, TEA: DIY Block Cipher, (2004) [2]
Paris Kitsos, Yan Zhang. “RFID Security: Techniques, Protocols and System-On-Chip Design” [3]
David J. Wheeler and Roger M. Needham. “Correction to xtea.” Technical report, Computer Laboratory, University of Cambridge, October 1998 (PDF) .
Roger M. Needham and David J. Wheeler. "Tea extensions." Technical report, Computer Laboratory, University of Cambridge, October 1997 (PDF) .
Test vectors for tea
JavaScript implementation of XXTEA with Base64
PHP implementation of XTEA
JavaScript implementation of TEA
Ruby implementation of XXTEA with Base64
LGPL Java / J2ME implementation of TEA
Visual Basic .NET implementation of TEA

[teasite-1] ¹ ² ³ ⁴ ⁵ TEA cipher page

[tea-2] ¹ ² ³ Roger M. Needham and David J. Wheeler. TEA, a Tiny Encryption Algorithm

[kelsey1996-3] Kelsey, John; Schneier, Bruce; Wagner, David. Key-schedule cryptanalysis of IDEA, G-DES, GOST, SAFER, and Triple-DES (English) // Lecture Notes in Computer Science: journal. - 1996. - Vol. 1109 . - P. 237-251 . - DOI : 10.1007 / 3-540-68697-5_19 .

[cryptoanalisys-4] ¹ ² Andem, Vikram Reddy (2003). A cryptoanalisys of the tiny encryption algorithm Archived on April 20, 2009.

[differential-5] Seokhie Hong, Deukjo Hong, Youngdai Ko, Donghoon Chang, Wonil Lee, Sangjin Lee, (2003). Differential Cryptanalysis of TEA and XTEA

[kelsey1997-6] Kelsey, John; Schneier, Bruce; Wagner, David. Related-key cryptanalysis of 3-WAY, Biham-DES, CAST, DES-X NewDES, RC2, and TEA (English) // Lecture Notes in Computer Science: journal. - 1997. - Vol. 1334 . - P. 233-246 . - DOI : 10.1007 / BFb0028479 .

[relatedkey-7] Eli Biham, Computer Science Department, Technion - Israel Institute of Technology, Haifa 32000, Israel, (1992). "New Types of Cryptanalytic Attacks Using Related Keys"

[impossible-8] Moon, Dukjae; Hwang, Kyungdeok; Lee, Wonil; Lee, Sangjin; Lim, Jongin. Impossible differential cryptanalysis of reduced round XTEA and TEA (English) // Lecture Notes in Computer Science: journal. - 2002. - Vol. 2365 . - P. 49-60 . - DOI : 10.1007 / 3-540-45661-9_4 .

[autogenerated1-9] ¹ ² Hong, Seokhie; Hong, Deukjo; Ko, Youngdai; Chang, Donghoon; Lee, Wonil; Lee, Sangjin. Differential cryptanalysis of TEA and XTEA (neopr.) // In Proceedings of ICISC 2003 .-- 2003.

[extended-10] Tom St Denis. Extended TEA Algorithms

[11] Original article with the implementation of the attack on XXTEA and an example code (unopened) (inaccessible link) Date of treatment November 6, 2009. Archived September 23, 2009.

[rteatests-12] Comparative stability results of symmetric cryptographic algorithms Archived July 25, 2008. (eng.)

[rka-13] A related key attack for RTEA. (inaccessible link)

[raidenhome-14] Raiden: An alternative to TEA Block Cipher

Tea