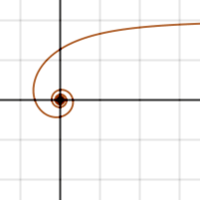
Hyperbolic spiral

Hyperbolic spiral for a = 2

A hyperbolic spiral is a flat transcendental curve . The hyperbolic spiral equation in the polar coordinate system is the inverse of the Archimedean spiral equation and is written as follows:

\rho \phi =a

{\ displaystyle \ rho \ phi = a}

{\ displaystyle \ rho \ phi = a}

The equation of the hyperbolic spiral in Cartesian coordinates:

x=\rho \cos \phi ,\qquad y=\rho \sin \phi ,

{\ displaystyle x = \ rho \ cos \ phi, \ qquad y = \ rho \ sin \ phi,}

{\ displaystyle x = \ rho \ cos \ phi, \ qquad y = \ rho \ sin \ phi,}

Parametric notation of the equation:

x=a{\cos t \over t},\qquad y=a{\sin t \over t},

{\ displaystyle x = a {\ cos t \ over t}, \ qquad y = a {\ sin t \ over t},}

{\ displaystyle x = a {\ cos t \ over t}, \ qquad y = a {\ sin t \ over t},}

The spiral has the asymptote y = a : for t, the ordinate tends to zero, tends to a , and the abscissa goes to infinity:

\lim _{t\to 0}x=a\lim _{t\to 0}{\cos t \over t}=\infty ,

{\ displaystyle \ lim _ {t \ to 0} x = a \ lim _ {t \ to 0} {\ cos t \ over t} = \ infty,}

{\ displaystyle \ lim _ {t \ to 0} x = a \ lim _ {t \ to 0} {\ cos t \ over t} = \ infty,}

\lim _{t\to 0}y=a\lim _{t\to 0}{\sin t \over t}=a\cdot 1=a.

{\ displaystyle \ lim _ {t \ to 0} y = a \ lim _ {t \ to 0} {\ sin t \ over t} = a \ cdot 1 = a.}

{\ displaystyle \ lim _ {t \ to 0} y = a \ lim _ {t \ to 0} {\ sin t \ over t} = a \ cdot 1 = a.}

Hyperbolic spiral

More articles: