Curve Zoom

Approximation of a curve having noise (random deviations) using an asymmetric peak model with an iterative process ( Gauss - Newton algorithm with a variable attenuation coefficient α).
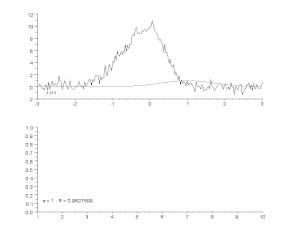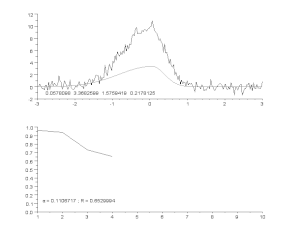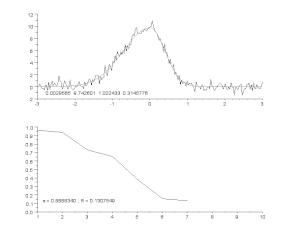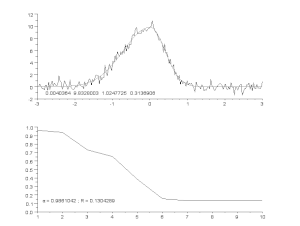
Above: source data and model.
Bottom: change in the normalized sum of squared deviations.

The approximation using curves ^[1] ^[2] is the process of constructing a curve or a mathematical function that best approaches the given points ^[3] with possible restrictions on the curve ^[4] . To construct such an approximation, one can use either interpolation ^[5] , where an exact passage of the curve through the points is required, or ^[6] ^[7] , when the “smoothing” function passes through the points approximately. A related section is regression analysis ^[8] ^[9] , which focuses mainly on questions of statistical inference , such as what kind of uncertainty lies in a curve that approximates data with some random errors. The constructed curves can be used to visualize the data ^[10] ^[11] , to calculate the values of the function at points where the value is not specified ^[12], and to determine the relationship between two or more variables ^[13] . Extrapolation means using the obtained curve beyond the data obtained from observation ^[14] , and gives rise to some uncertainty ^[15] , because it may depend on the method of constructing the curve.

Content

Different types of approximation using curves

Approximation of given points by functions

Most often, an approximation is sought in the form y = f ( x ) .

Approximation of given points by linear and polynomial functions

Approximation of points generated by the sine function, polynomial functions.
The red line is a polynomial of the first degree , the green line is of the second degree , the orange line is of the third degree , and the blue is of the fourth degree

We begin the approximation with a polynomial of the first degree:

y=ax+b\;.

{\ displaystyle y = ax + b \ ;.}

This is a line with an angular coefficient a . A straight line can be drawn through any two points, so that a polynomial of the first degree passes through any two points with different abscissas .

If the order of the equation is increased to polynomials of the second degree, we obtain:

y=ax^{2}+bx+c\;.

{\ displaystyle y = ax ^ {2} + bx + c \ ;.}

This function describes a parabola . A parabola can be drawn through any three points.

If we increase the order of the polynomial to the third degree, we get:

y=ax^{3}+bx^{2}+cx+d\;.

{\ displaystyle y = ax ^ {3} + bx ^ {2} + cx + d \ ;.}

Such a curve can be constructed for any four given points. Moreover, as a rule, such a curve can be constructed if exactly four constraints are specified. Each constraint can be a point, angle , or curvature (which is the reciprocal of the radius of the circle in contact ). Constraints in the form of angle and curvature are most often added to the ends of the curve, and such constraints are often called boundary conditions . The same boundary conditions are often used to ensure a smooth transition between polynomial curves within the spline . Higher order constraints, such as the rate of change of curvature, can also be specified. This, for example, can be used in the construction of motorway junctions to calculate the rate of change of forces acting on the car (see jerk ) during the passage of the junction and calculate the maximum permissible speed.

A polynomial of the first degree can also be constructed if one point and an angle are given, while a polynomial of the third degree can be constructed for two points, a given angular coefficient and a given curvature. Other combinations of restrictions are possible for these and higher degrees of the polynomial.

If more than n + 1 conditions are specified (where n is the degree of the polynomial), one can still try to construct a polynomial curve satisfying these conditions. However, in the general case, such a curve cannot be constructed (for example, a polynomial of the first degree at three points can be constructed only if these points are collinear ). Therefore, some approximation methods are needed. The least squares method is one of them.

There are several reasons for obtaining an approximate solution when simply increasing the degree of the polynomial would give an exact passage through the points:

Even if an exact solution exists, it does not follow from this that it is easy to find. In some algorithms, we can get a divergent sequence and the exact solution may not be computable; in other cases, it may take too much computer time to find the exact solution. In these situations, an approximate solution may be more acceptable.
The effect of averaging unreliable data in a sample may be preferable to accurately following the sample points at which a curve may bend.
Runge phenomenon : when interpolating by polynomials of high degrees, the effect of unwanted oscillations can occur. If the curve passes through points A and B , the curve is expected to pass somewhere close to the middle of segment AB . This may turn out to be wrong in the case of polynomials of high degree - the deviation can be very large. For polynomials of small degree, the curve is likely to pass near the middle of the segment (and in the case of a polynomial of the first degree, it will certainly go through the middle).
Low degree polynomials are usually “smooth” and high degree polynomials are usually “wavy”. More specifically, the maximum number of inflection points of a polynomial curve is n-2 , where n is the order of the polynomial. The inflection point is the point where the curvature of the curve changes sign. Note that polynomials of a high degree are not necessarily “wavy”, they can also be “smooth”, but there are no guarantees of “smoothness”, unlike polynomials of small order. A tenth degree polynomial can have up to eight inflection points, but it can have less, or not at all.

The degree of the polynomial, higher than necessary for the exact passage of the curve through the points, is undesirable for all the reasons listed above, but, in addition, leads to an infinite number of solutions. For example, a polynomial of the first degree (line) with the restriction to one point instead of the usual two leads to an infinite number of solutions. Hence the problem arises - how to compare and choose only one solution, and this can become a problem for both programs and people. For this reason, the best choice is the smallest degree possible for the exact fulfillment of all restrictions, and maybe even the lesser degree if an approximate solution is acceptable.

Approximation of given points by other functions

Other types of curves, such as trigonometric functions (e.g., sine and cosine), can also be used in some cases.

In spectroscopy, data can be approximated by the normal distribution , the Cauchy distribution , the , and related functions.

Algebraic approximation and geometric approximation by curves

For algebraic data analysis, “approximation” usually means finding a curve that minimizes the vertical (along the y axis) deviation of a point from the curve (for example, the least squares method ). For graphic applications and when working with images, the geometric approximation seeks the best visual approximation, which usually means trying to minimize the distance to the curve (for example, the least full square method ) or to minimize deviations in both coordinates. The geometric approximation is unpopular, because it usually involves non-linear and / or recurrent calculations, although it gives an aesthetically more acceptable and geometrically more accurate result ^[16] ^[17] ^[18] .

Approximation of given points by flat curves

If the function cannot be specified as $y=f(x)$ ${\ displaystyle y = f (x)}$ , you can try to zoom in using a flat curve .

In some cases, other types of curves can be used, such as conical sections (arcs of a circle, ellipse, parabola and hyperbola) or trigonometric functions (such as sine and cosine). For example, the trajectories of objects under the influence of gravity are parabolas (if air resistance is not taken into account). Thus, linking (experimental) trajectory points to a parabolic curve will make sense. The tides correspond to the sinusoidal model, so tide data should be compared with the sine or the sum of two sines of different periods, given the effects of both the moon and the sun.

In the case of a parametric curve, it is effective to consider each coordinate as a separate function of the length of the curve . If the source data can be ordered, the chord length can be used ^[19] .

Geometric approximation of given points by a circle

Circle approximation using the Kuup method (Coope). The points correspond to an arc of a circle centered at (1, 1) and a radius of 4.

Different ellipse models

Elliptic approximation with minimization of algebraic distance (FitzGibbon method).

Coop ^[20] tried to solve the problem of finding the best visual approximation by a circle of points on a plane. The method elegantly converts a non-linear problem into a linear one, which can already be solved without resorting to recurrent methods, and therefore the result is faster than using the previous approaches.

Geometric approximation by ellipse

The aforementioned technique was extended to ellipses of a general form ^[21] by adding a nonlinear step, as a result of which a fast method was obtained that finds, however, visually attractive ellipses of arbitrary orientation and location.

Surface

Note that although the discussion so far has concerned flat curves, most of the results extend to surfaces in three-dimensional space, each piece of which is defined by a grid of curves in two parametric directions. A surface may consist of one or more pieces in both directions.

Programs

Many , such as R , and , such as the GNU Scientific Library , , DataMelt , Maple , MATLAB , SciPy, and OpenOpt include curve fitting tools for various scenarios. There are also programs specially written to approximate curves. They can be found in the articles " " and " ".

Notes

↑ Arlinghaus, 1994 .
↑ Kolb, 1984 .
↑ Halli, Rao, 1992 , p. 165.
↑ Silver, 2012 .
↑ Kiusalaas, 2005 , p. 21.
↑ Guest, 2012 , p. 349.
↑ See also: Smoothing Operator
↑ Campaign Package. Documentation: “Fitting Models to Biological Data Using Linear and Nonlinear Regression” (Harvey Motulsky, Arthur Christopoulos).
↑ Freund, Wilson, Sa, 2006 , p. 269.
↑ Daud, Sagayan, Yahya, Najwati, 2009 , p. 689.
↑ Hauser, 2009 , p. 227.
↑ Williams, 1976 , p. 150.
↑ Salkind, 2010 , p. 266.
↑ Klosterman, 1990 , p. one.
↑ Yoe, 1996 , p. 69.
↑ Ahn, 2008 .
↑ Chernov, Ma, 2011 , p. 285-302.
↑ Liu, Wang, 2008 , p. 384–397.
↑ Ahlberg, Nilson, Walsh, 1967 , p. 51.
↑ Coope, 1993 , p. 381.
↑ Sheer, 1997 .

Literature

Sandra Lach Arlinghaus. Practical Handbook of Curve Fitting. - CRC Press, 1994 .-- ISBN 0849301434 .
William M. Kolb. Curve Fitting for Programmable Calculators. - 3. - Syntec, Incorporated, 1984. - ISBN 0943494028 .
John R. Hauser. Numerical Methods for Nonlinear Engineering Models. - Springer, 2009 .-- ISBN 978-1-4020-9919-9 .
ID Coope. Circle fitting by linear and nonlinear least squares // Journal of Optimization Theory and Applications. - 1993. - T. 76 , no. 2 . - S. 381 . - DOI : 10.1007 / BF00939613 .
Encyclopedia of Research Design / Neil J. Salkind. - SAGE Publications, 2010. - T. 1. - ISBN 978-1-4129-6127-1 .
Rudolf J. Freund, William J. Wilson, Ping Sa. Regression Analysis / Statistical Modeling of a Response Variable. - 2. - Elsevier, 2006. - ISBN 0-12-088597-2 .
Jaan Kiusalaas . Numerical Methods in Engineering with MATLAB®. - Cambridge University Press, 2005. - ISBN 0-521-85288-9 .
Richard E. Klosterman. Community Analysis and Planning Techniques. - Rowman & Littlefield Pub Inc, 1990. - ISBN 084767651X .
Hanita Daud, Vijanth Sagayan, Noorhana Yahya, Wan Najwati. Visual Informatics: Bridging Research and Practice (IVIC 2009) / Halimah Badioze Zaman, Peter Robinson, Maria Petrou, Patrick Olivier, Heiko Schröder, Timothy K. Shih. - Berlin, Heidelberg, New York: Sprintger, 2009.- T. 5857. - (Lecture Notes in Computer Science). - ISBN 3-642-05035-2 .
An Introduction to Risk and Uncertainty in the Evaluation of Environmental Investments / Charles E. Yoe. - West Chester, Pensylvania: The Greeley-Polhemus Group, Inc., 1996.
PG Guest. Numerical Methods of Curve Fitting. - Cambridge Academ, 2012 .-- ISBN 978-1-107646-5-7 .
SS Halli, KV Rao. Advanced Techniques of Population Analysis. - 1992. - S. 165. - ISBN 0306439972 .
Sung-Joon Ahn. Geometric Fitting of Parametric Curves and Surfaces // Journal of Information Processing Systems. - 2008. - December (vol. 4 ( issue 4 ). - DOI : 10.3745 / JIPS.2008.4.4.153 . Archived on March 13, 2014.
JH Ahlberg, EN Nilson, JL Walsh. The theory of splines and their applications . - New York, London: Academic Press, 1967.
N. Chernov, H. Ma. Computer Vision / Sota R. Yoshida. - Nova Science Publishers, 2011 .-- S. 285-302. - ISBN 9781612093994 .
Nate Silver. The Signal and the Noise: Why So Many Predictions Fail-but Some Don't. - Penguin Group, 2012. - ISBN 978-1-59-420411-1 .
Dudley Williams. Spectroscopy / Claire Marton .. - Academic Press, 1976. - T. 13, Part 1. - (Methods of Experimental Physics). - ISBN 0124759130 .
Yang Liu, Wenping Wang. Advances in Geometric Modeling and Processing / F. Chen, B. Juttler. - 2008 .-- T. 4975 . - S. 384–397 . - ISBN 978-3-540-79245-1 . - DOI : 10.1007 / 978-3-540-79246-8_29 .
P. Sheer. A Software Assistantfor Manual Stereo Photometrology. - University of the Witwater-srand, 1997.