| {3,3,3} | {3,3,4} | {4,3,3} |
|---|---|---|
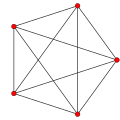 Pentecost 4- simplex |  Sixteen cell Orthoplex 4- orthoplex |  Tesseract 4- cube |
| {3,4,3} | {5,3,3} | {3,3,5} |
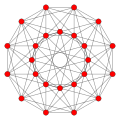 Octaplex Twenty-four-cell |  Dodecaplex Centenary |  Tetraplex Six hundredth |
In geometry, a 4-dimensional polyhedron is a polyhedron in four-dimensional space [1] [2] . A polyhedron is a connected closed figure, consisting of polyhedral elements of smaller dimension - vertices , edges , faces ( polygons ) and ( 3-dimensional polyhedra ). Each face belongs to exactly two cells.
The two-dimensional analogue of 4-dimensional polyhedra is the polygon , and the three-dimensional analogue is the (three-dimensional) polyhedron .
Topologically, 4-dimensional polyhedra are closely related to , such as , tiling a 3-dimensional space. Similarly, a three-dimensional cube is connected with infinite two-dimensional square cells . Convex 4-dimensional polyhedra can be cut and expanded in the form of unfoldings in 3-dimensional space.
Content
Definition
A 4-dimensional polyhedron is a closed four-dimensional figure. It consists of vertices (corner points), edges , faces, and . A cell is a three-dimensional analogue of a face and is a (3-dimensional) polyhedron . Each (2-dimensional) face must connect exactly two cells, in the same way as the edges of a three-dimensional polyhedron connect exactly two faces. Like other polyhedra, elements of a 4-dimensional polyhedron cannot be divided into two or more sets, which are also 4-polyhedra, that is, it is not composite.
The most famous 4-dimensional polyhedron is a tesseract (hypercube), a four-dimensional analogue of a cube.
Visualization
| Slice | Scan | |
|---|---|---|
| Projections | ||
| Schlegel | 2D orthogonal | 3D orthogonal |
4-dimensional polyhedra cannot be represented in three-dimensional space due to excess dimension. A number of techniques are used for visualization.
- Orthogonal projection
Orthogonal projections can be used to show different symmetries of a 4-dimensional polyhedron. Projections can be represented as two-dimensional graphs, or can be represented as three-dimensional bodies as .
- Perspective projection
Just like three-dimensional shapes can be projected onto a flat sheet, 4-dimensional shapes can be projected into 3-dimensional space, or even onto a plane. A common type of projection is the Schlegel diagram , which uses the stereographic projection of points on the surface of a 3-sphere in three-dimensional space, connected in 3-dimensional space by straight edges, faces and cells.
- Slice
Just as a cut of a polyhedron reveals a cut surface, a cut of a 4-dimensional polyhedron gives a “hypersurface” in three-dimensional space. The sequence of such slices can be used to understand the whole figure. Extra dimension can be equated to time for the formation of animation of these sections.
- Reamers
The development of a 4-dimensional polyhedron consists of polyhedral connected by faces and located in three-dimensional space, just as the polygonal development faces of a three-dimensional polyhedron are connected by edges and are all in the same plane.
Topological characteristics
The topology of any given 4-polyhedron is determined by its Betty numbers and [3] .
The value of the Euler characteristic used to characterize polyhedra is not properly generalized to higher dimensions and is equal to zero for all 4-dimensional polytopes, whatever the underlying topology. This mismatch of the Euler characteristics for a reliable distinction between different topologies in high dimensions leads to the appearance of more refined Betty numbers [3] .
Similarly, the concept of orientability of a polyhedron is not enough to characterize the twisting of surfaces of toroidal polyhedra, which leads to the use of torsion coefficients [3] .
Classification
Criteria
4-dimensional polyhedra can be classified by properties, such as “ convexity ” and “ symmetry ” [3] .
- A 4-dimensional polyhedron is convex if its boundaries (including cells, (3-dimensional) faces and edges) do not intersect themselves (in principle, the faces of a polyhedron can pass inside the shell) and the segments connecting any two points of the four-dimensional polyhedron are completely inside him .. Otherwise, the polyhedron is considered non-convex . Self-intersecting 4-dimensional polyhedra are also known as star-shaped polyhedra by analogy with star- like forms of non - convex Kepler-Poinsot polyhedra .
- A 4-dimensional polyhedron is correct if it is transitive with respect to its flags . This means that all its cells are congruent regular polyhedra , and also all its vertex figures are congruent to another kind of regular polyhedra.
- A convex 4-polyhedron is semiregular if it has a symmetry group such that all vertices are equivalent ( vertex transitive ) and the cells are regular polyhedra . Cells can be two or more types, provided that they have the same kind of faces. There are only 3 such figures found by in 1900 - a , and .
- A 4-polyhedron is if it has a symmetry group in which all vertices are equivalent and the cells are . The faces (2-dimensional) of a homogeneous 4-polyhedron must be regular polygons .
- A 4-polyhedron is an [4] if it is vertex transitive and has edges of the same length. That is, inhomogeneous cells, for example, convex Johnson polyhedra , are allowed.
- The regular 4-dimensional polyhedron, which is also convex , is spoken of as the .
- A 4-dimensional polyhedron is prismatic if it is a direct product of two or more polyhedra of smaller dimension. A prismatic 4-dimensional polyhedron is homogeneous if its factors in the direct product are homogeneous. The hypercube is prismatic (the product of two squares or a cube and a segment ), but is considered separately, since it has higher symmetry than the symmetries inherited from the factors.
- a mosaic or honeycomb in three-dimensional space is the decomposition of three - dimensional Euclidean space into a repeating polyhedral cells. Such mosaics or tilings are infinite and not limited by the “4D” volume, so they are examples of infinite 4-polyhedra. A homogeneous mosaic of 3-dimensional space is a mosaic in which the vertices are congruent and connected by a crystallographic group , and the cells are .
Classes
The following list of different categories of 4-dimensional polyhedra is classified according to the criteria set out above:
( vertex-transitive ):
- Convex homogeneous 4-dimensional polyhedra (64, plus two infinite families)
- 47 non-prismatic convex homogeneous 4-dimensional polyhedra include:
- 6 regular 4-dimensional polyhedra
- :
- {} × {p, q}: 18 (including cubic hyperprisms, regular hypercubes )
- Prisms built on antiprisms (endless family)
- {p} × {q}: Duoprisms (infinite family)
- 47 non-prismatic convex homogeneous 4-dimensional polyhedra include:
- Non-convex homogeneous 4-dimensional polyhedra (10 + unknown)With its 600 vertices, the is the largest of 10 regular star-shaped 4-dimensional polyhedra
- 10 (correct)
- 57 hyperprisms built on non-convex homogeneous polyhedra
- An unknown number of non-convex homogeneous 4-dimensional polyhedra - and other co-authors found 1849 polyhedra (convex and star-shaped), all built on vertex shapes using the program [5]
Other convex 4-dimensional polyhedra :
Infinite homogeneous 4-dimensional polyhedra in Euclidean 3-dimensional space (homogeneous tilings by convex homogeneous cells)
- 28 (homogeneous convex tilings), including:
- 1 correct tiling, : {4,3,4}
Infinite homogeneous 4-polyhedra of hyperbolic 3-dimensional space (homogeneous tilings by convex homogeneous cells)
- 76 Withhoff , including:
- 4 regular tilings of a compact hyperbolic 3-dimensional space : {3,5,3}, {4,3,5}, {5,3,4}, {5,3,5}
Dual ( ):
- 41 unique dual homogeneous 4-dimensional polyhedra
- 17 unique dual homogeneous multifaceted prisms
- infinite family of dual convex homogeneous duoprisms (with irregular tetrahedral cells)
- 27 unique dual homogeneous cells, including:
Others:
- periodic cell-filling cells with irregular cells
:
These categories include only 4-dimensional polygons with a high degree of symmetry. Many other 4-dimensional polyhedra may exist, but they have not been studied as intensively as the ones listed above.
See also
- The correct four-dimensional polyhedron
- The 3-sphere is another widely discussed figure located in four-dimensional space. But it is not a 4-dimensional polyhedron, since it is not limited to polyhedral cells.
- is a figure in 4-dimensional space associated with duoprisms , although it is also not a polyhedron.
Notes
- ↑ Vialar, 2009 , p. 674.
- ↑ Capecchi, Buscema, D'Amore, 2010 , p. 598.
- ↑ 1 2 3 4 Richeson, D .; Euler's Gem: The Polyhedron Formula and the Birth of Topoplogy , Princeton, 2008.
- ↑ The English word uses the word scaliform , formed from two words - scale (a multi-valued word, here - size, scale) and uniform (homogeneous). Title suggested by Jonathan Bowers
- ↑ Uniform Polychora , Norman W. Johnson (Wheaton College), 1845 cases in 2005
Literature
- T. Vialar. Complex and Chaotic Nonlinear Dynamics: Advances in Economics and Finance. - Springer, 2009 .-- S. 674. - ISBN 978-3-540-85977-2 .
- V. Capecchi, P. Capecchi, M. Buscema, B. D'Amore. Applications of Mathematics in Models, Artificial Neural Networks and Arts. - Springer, 2010 .-- S. 598. - ISBN 978-90-481-8580-1 . - DOI : 10.1007 / 978-90-481-8581-8 .
- HSM Coxeter :
- HSM Coxeter, MS Longuet-Higgins, JCP Miller: Uniform Polyhedra , Philosophical Transactions of the Royal Society of London, Londne, 1954
- HSM Coxeter . . - 3rd (1947, 63, 73). - New York: Dover Publications Inc., 1973. - ISBN 0-486-61480-8 .
- HSM Coxeter . Kaleidoscopes: Selected Writings of HSM Coxeter / F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss. - Wiley-Interscience Publication, 1995. - ISBN 978-0-471-01003-6 .
- (Paper 22) HSM Coxeter, Regular and Semi Regular Polytopes I , [Math. Zeit. 46 (1940) 380-407, MR 2.10]
- (Paper 23) HSM Coxeter, Regular and Semi-Regular Polytopes II , [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) HSM Coxeter, Regular and Semi-Regular Polytopes III , [Math. Zeit. 200 (1988) 3-45]
- JH Conway , MJT Guy. Proceedings of the Colloquium on Convexity at Copenhagen. - 1965. - S. 38-39.
- The Theory of Uniform Polytopes and Honeycombs. - Ph.D. Dissertation. - University of Toronto, 1966.
- Four-dimensional Archimedean Polytopes (German), Marco Möller, 2004 PhD dissertation [1]
Links
- Weisstein, Eric W. Polychoron on Wolfram MathWorld .
- Weisstein, Eric W. Polyhedral formula on the Wolfram MathWorld website.
- Weisstein, Eric W. Regular polychoron Euler characteristics ( Wolfram MathWorld) . *
- Four dimensional figures page
- Polychoron on Glossary for Hyperspace
- Uniform Polychora , Jonathan Bowers
- Uniform polychoron Viewer - Java3D Applet with sources
- Dr. R. Klitzing, polychora