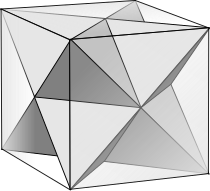
Stellated Octahedron as a Cube Cut
In geometry, a cut is the process of removing part of a polygon or polyhedron without creating new vertices .
New edges of a faceted polyhedron can be created along the or . A faceted polyhedron will have two faces for each edge and is a new polyhedron or a connection of polyhedrons.
Cutting is the reverse or dual formation of a stellate shape . For each stellate form of a convex polyhedron, there is a dual faceting of the dual polyhedron .
Content
Faceted Polygons
For example, a regular pentagon has one symmetrical facet, pentagrams , and a regular hexagon has two symmetric facets, one of them is a polygon, and the other is a union of two triangles.
| Convex | ||
|---|---|---|
| Regular pentagon {five} | Regular hexagon {6} | |
| Correct | Quasi-correct | Correct connections |
| Pentagram {5/2} | Star hexagon | hexagram {6/2} |
Faceted Polyhedrons
A regular icosahedron can be cut to three regular Kepler polyhedra - Poinsot - a small stellated dodecahedron, a large dodecahedron and a large icosahedron. They have 30 edges.
| Convex | Right stars | ||
|---|---|---|---|
| icosahedron | Big dodecahedron | Small Star Dodecahedron | Big icosahedron |
A regular dodecahedron can be faceted up to one regular Kepler-Poinsot polyhedron , three homogeneous star-shaped polyhedra, and three polyhedron connections . Homogeneous stars and the are built on the . is cut with star-shaped octagram faces.
| Convex | Right stars | Homogeneous stars | Vertex transitive | ||
|---|---|---|---|---|---|
| dodecahedron | large stellate dodecahedron | ||||
| Convex | Correct connections | ||
|---|---|---|---|
| dodecahedron | five tetrahedra | ||
History
Cutting was not studied as intensively as the formation of a stellate form .
- In 1619, Kepler described the correct connection of two tetrahedrons enclosed in a cube, which he called Stella octangula . This seems to be the first known example of a cut.
- In 1858, Bertrand obtained regular star-shaped polyhedra ( Kepler-Poinsot bodies ) by cutting regular convex icosahedrons and dodecahedrons .
- In 1974, Bridge listed several facets of regular polyhedra, including dodecahedron facets.
- In 2006, Incibald described the basic theory of cut patterns for polyhedra. For a given vertex, the diagram shows possible edges and facets (new faces) that can be used to cut the original shell. This diagram is dual to the star-shaped diagram of the dual polyhedron, which shows all possible edges and vertices for some plane of the face of the original kernel.
Notes
Literature
- J. Bertrand. Note sur la théorie des polyèdres réguliers // Comptes rendus des séances de l'Académie des Sciences. - 1858. - T. 46 . - S. 79-82 .
- NJ Bridge. Facetting the dodecahedron // Acta crystallographica. - 1974.- T. A30 . - S. 548–552 .
- G. Inchbald. Facetting diagrams // The mathematical gazette. - 2006 .-- T. 90 . - S. 253—261 .
- Alan Holden. Shapes, Space, and Symmetry. - New York: Dover, 1991 .-- T. 94.