Pentagonal hexahedron

Pentagonal hexahedron
Pentagonal hexahedron
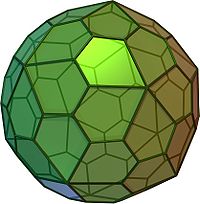	; The "right" option ; ( rotating model , 3D model )
	; "Left" option ; ( rotating model , 3D model )
Type of	catalan body
The properties	convex , isohedral , chiral
Combinatorics
60 faces; 150 ribs; 92 peaks	Χ = 2
Facets	irregular pentagons:;
Vertex configuration	20 + 60 (5 3 ); 12 (5 5 )
Face configuration	V3.3.3.3.5
Dual polyhedron	snub dodecahedron
	Scan ; Sweep for the "left" option
Classification
Designations	gD
Symmetry group	I (chiral icosahedral)

The pentagonal hexecontahedron (from other Greek πέντε is “five”, γωνία is “angle”, ἑξήκοντα is “sixty” and ἕδρα is “face”) is a semiregular polyhedron (Catalan body), dual to the snub-dodecahedron . Composed of 60 identical irregular pentagons .

Has 92 peaks. In 12 peaks (located in the same way as the tops of the icosahedron ), 5 faces converge along their sharp angles; in 20 vertices (located in the same way as the vertices of the dodecahedron ), 3 faces converge along those obtuse angles that are farther from the sharp; in the remaining 60 peaks, two faces converge with their obtuse angles close to an acute one, and one with an obtuse angle farthest from an acute one.

12 peaks are located just like the tops of the icosahedron
20 vertices are located just like the vertices of a dodecahedron

The pentagonal hexecontahedron has 150 edges - 60 “long” and 90 “short”.

Unlike most other catalan bodies, the pentagonal hexecontahedron (along with the pentagonal icositetrahedron ) is chiral and exists in two different mirror-symmetric (enantiomorphic) versions - “right” and “left”.

Metric specifications and angles

In determining the metric properties of the pentagonal hexecontahedron, it is necessary to solve cubic equations and use cubic roots - whereas for achiral catalan bodies, nothing more complicated than square equations and square roots is required. Therefore, the pentagonal hexecontahedron, unlike most other Catalan bodies, does not allow Euclidean construction . The same is true for the pentagonal icocitetrahedron, as well as for archimedean bodies dual to it.

In the formulas below, the constant $\xi$ ${\ displaystyle \ xi}$ Is the only real root ^{[1] of the} equation

8x^{3}+8x^{2}-\Phi ^{2}=0,

{\ displaystyle 8x ^ {3} + 8x ^ {2} - \ Phi ^ {2} = 0,}

Where $\Phi ={\frac {1+{\sqrt {5}}}{2}}$ ${\ displaystyle \ Phi = {\ frac {1 + {\ sqrt {5}}} {2}}}$ - ratio of the golden ratio; this root is equal

\xi ={\frac {1}{12}}\left({\sqrt[{3}]{44+12\Phi \,(9+{\sqrt {81\Phi -15}})}}+{\sqrt[{3}]{44+12\Phi \,(9-{\sqrt {81\Phi -15}})}}-4\right)\approx 0{,}4715756.

{\ displaystyle \ xi = {\ frac {1} {12}} \ left ({\ sqrt [{3}] {44 + 12 \ Phi \, (9 + {\ sqrt {81 \ Phi -15}}) }} + {\ sqrt [{3}] {44 + 12 \ Phi \, (9 - {\ sqrt {81 \ Phi -15}})}} - 4 \ right) \ approx 0 {,} 4715756.}

Edge of the pentagonal hexecahedron

If the three “short” sides of the face have a length $b$ ${\ displaystyle b}$ , then the two “long” sides have a length

a={\frac {1+2\xi }{2(1-2\xi ^{2})}}b\approx 1{,}7498526b.

{\ displaystyle a = {\ frac {1 + 2 \ xi} {2 (1-2 \ xi ^ {2})}} b \ approx 1 {,} 7498526b.}

The surface area and volume of the polyhedron are expressed as

S={\frac {30(2+3\xi ){\sqrt {1-\xi ^{2}}}}{1-2\xi ^{2}}}\;b^{2}\approx 162{,}6989642b^{2},

{\ displaystyle S = {\ frac {30 (2 + 3 \ xi) {\ sqrt {1- \ xi ^ {2}}}} {1-2 \ xi ^ {2}}};; b ^ {2 } \ approx 162 {,} 6989642b ^ {2},}

V={\frac {5(1+\xi )(2+3\xi )}{(1-2\xi ^{2}){\sqrt {1-2\xi }}}}\;b^{3}\approx 189{,}7898521b^{3}.

{\ displaystyle V = {\ frac {5 (1+ \ xi) (2 + 3 \ xi)} {(1-2 \ xi ^ {2}) {\ sqrt {1-2 \ xi}}}} \ ; b ^ {3} \ approx 189 {,} 7898521b ^ {3}.}

The radius of the inscribed sphere (touching all faces of the polyhedron at their centers of inscribed circles ) will be equal to

r={\frac {1}{2}}{\sqrt {\frac {1+\xi }{(1-\xi )(1-2\xi )}}}\;b\approx 3{,}4995278b,

{\ displaystyle r = {\ frac {1} {2}} {\ sqrt {\ frac {1+ \ xi} {(1- \ xi) (1-2 \ xi)}}};; b \ approx 3 {,} 4995278b,}

radius of a half-inscribed sphere (touching all edges) -

\rho ={\sqrt {\frac {1+\xi }{2(1-2\xi )}}}\;b\approx 3{,}5976248b,

{\ displaystyle \ rho = {\ sqrt {\ frac {1+ \ xi} {2 (1-2 \ xi)}}};; b \ approx 3 {,} 5976248b,}

the radius of the circle inscribed on the face -

r_{\Gamma \mathrm {P} }={\sqrt {\rho ^{2}-r^{2}}}={\frac {1}{2}}{\sqrt {\frac {1+\xi }{1-\xi }}}\;b\approx 0{,}8343915b,

{\ displaystyle r _ {\ Gamma \ mathrm {P}} = {\ sqrt {\ rho ^ {2} -r ^ {2}}} = {\ frac {1} {2}} {\ sqrt {\ frac { 1+ \ xi} {1- \ xi}}} \; b \ approx 0 {,} 8343915b,}

face diagonal parallel to one of the “short” sides -

e=(1+2\xi )b\approx 1{,}9431513b.

{\ displaystyle e = (1 + 2 \ xi) b \ approx 1 {,} 9431513b.}

It is impossible to describe a sphere near the pentagonal hexecontahedron so that it passes through all the vertices.

All four obtuse corners of the face are equal $\arccos \,(-\xi )\approx 118{,}14^{\circ };$ ${\ displaystyle \ arccos \, (- \ xi) \ approx 118 {,} 14 ^ {\ circ};}$ the acute angle of the face (between the "long" sides) is $\arccos \,(8\xi ^{2}-8\xi ^{4}-1)\approx 67{,}45^{\circ }.$ ${\ displaystyle \ arccos \, (8 \ xi ^ {2} -8 \ xi ^ {4} -1) \ approx 67 {,} 45 ^ {\ circ}.}$

The dihedral angle at any edge is the same and equal $\arccos \,{\frac {\xi }{\xi -1}}\approx 153{,}18^{\circ }.$ ${\ displaystyle \ arccos \, {\ frac {\ xi} {\ xi -1}} \ approx 153 {,} 18 ^ {\ circ}.}$

Notes

↑ See the roots of this equation .

Links

Weisstein, Eric W. The Pentagon HexaContahedron on Wolfram MathWorld .

[1] See the roots of this equation .

Pentagonal hexahedron

Metric specifications and angles

Notes

Links

More articles: