In geometry, a bicupole is a body formed by connecting two domes at the base.
| Lots of bicupoles | ||
|---|---|---|
 Example: cuboctahedron | ||
| Type of | Johnson's Polyhedron | |
| The properties | convex | |
| Combinatorics | ||
| Items |
| |
| Facets | 2 n triangles 2 n squares 2 n- gons | |
| Classification | ||
| Symmetry group | Ortho: D n h , [2, n], * n22, order 4 n Gyro: D n d , [2 + , 2n], 2 * n, order 4 n | |
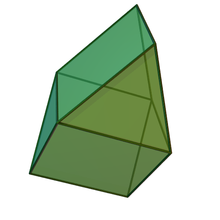
There are two classes of bicupoles, since each dome (half of a polyhedron) has intermittent triangles and squares along its perimeter. If the same types of faces are in contact, the result will be an ortho-dome (or a straight bicupole), if the squares are adjacent to the triangles, the result will be a gyro-dome (or a rotated bicupole).
Domes and bicupoles exist as infinite sets of polyhedra, just like sets of pyramids , bipyramids , prisms and trapezhedrons .
Six bicupoles have regular polygons as faces - these are triangular , square and pentagonal ortho- and gyrocups. The triangular gyrocupole is an Archimedean body ( cuboctahedron ). The other five are Johnson's polyhedra .
Bicupoles of higher orders can be constructed if lateral faces can be stretched into rectangles and isosceles triangles .
Bicupoles are specific polytopes having four faces adjacent to any vertex. This means that their dual polyhedra will have all faces quadrangular . The most famous example is the rhombic dodecahedron , which consists of 12 rhombic faces. The dual polyhedron of the orthoform, the , is a dodecahedron similar to a rhombic dodecahedron , but it has 6 trapezoidal faces that alternate and form a ring.
Content
Views
Many orthobic domes
| Symmetry | Picture | Description |
|---|---|---|
| D 2h [2.2] * 222 | Diagonal orthobicupole or bifastigium : 4 triangles (coplanar pairs), 4 squares | |
| D 3h [2,3] * 223 | J : 8 triangles, 6 squares. Dual is the | |
| D 4h [2,4] * 224 | J : 8 triangles, 10 squares | |
| D 5h [2,5] * 225 | J : 10 triangles, 10 squares, 2 pentagons | |
| D nh [2, n ] * 22n | n- angular orthobic dome: 2 n triangles, 2 n squares, 2 n- gons |
Many gyrobic domes
| Symmetry | Picture | Description |
|---|---|---|
| D 2d [2 +, 4] 2 * 2 | Gyrobifastigium (J 26 ): 4 triangles, 4 squares | |
| D 3d [2 +, 6] 2 * 3 | Triangular gyrobic dome or octahedron : 8 triangles, 6 squares. Its dual is the rhombododecahedron | |
| D 4d [2 +, 8] 2 * 4 | J : 8 triangles, 10 squares | |
| D 5d [2 +, 10] 2 * 5 | (J 31 ): 10 triangles, 10 squares, 2 pentagons | |
| D nd [2 +, 2n] 2 * n | n- angular gyrobic dome: 2 n triangles, 2 n squares, 2 n- gons |
Notes
- Convex Solids with Regular Faces. - Canadian Journal of Mathematics. - 1966. - T. 18. - S. 169–200. It contains a listing of 92 bodies and the hypothesis that there are no others.
- [Zalgaller, Victor Abramovich. Convex Polyhedra with Regular Faces. - Consultants Bureau, 1969. First evidence that there are only 92 Johnson bodies.
- V.A. Zalgaller. Convex polyhedra with regular faces // Zap. scientific sem. LOMI. - 1967. - T. 2 . Proof that there are only 92 Johnson bodies.