Fractal dimension

11.5 x 200 = 2300 km

28 x 100 = 2800 km

70 x 50 = 3,500 km

Figure 1. The total length of the UK coastline increases when the length of the measuring stick (pole) decreases ^[1] .

Fractal dimension ( English fractal dimension ) - one of the ways to determine the dimension of a set in metric space . The fractal dimension of an n- dimensional set can be determined using the formula:

D=-\lim \limits _{\varepsilon \to 0}{\frac {\ln(N_{\varepsilon })}{\ln(\varepsilon )}}

{\ displaystyle D = - \ lim \ limits _ {\ varepsilon \ to 0} {\ frac {\ ln (N _ {\ varepsilon})} {\ ln (\ varepsilon)}}}

{\ displaystyle D = - \ lim \ limits _ {\ varepsilon \ to 0} {\ frac {\ ln (N _ {\ varepsilon})} {\ ln (\ varepsilon)}}}

where

N_{\varepsilon }

{\ displaystyle N _ {\ varepsilon}}

N_ \ varepsilon

- the minimum number of n- dimensional "balls" of radius

\varepsilon

{\ displaystyle \ varepsilon}

\ varepsilon

needed to cover the set.

Fractal dimension can take a non-integer numerical value ^[2] .

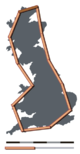
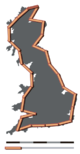
The basic idea of “fractional” ( English fractured ) dimension has a long history in mathematics, but it was the term itself that was introduced into circulation by Benoit Mandelbrot in 1967 in on self-similarity , in which he described the “fractional” ( English fractional) ) dimension ^[3] . In this article, Mandelbrot referred to a previous work by Lewis Fry Richardson describing the idea contrary to common sense that the measured coastline length depends on the length of the measuring stick (pole) ( see Fig. 1 ). Following this idea, the fractal dimension of the coastline corresponds to the ratio of the number of poles (on a certain scale) needed to measure the length of the coastline to the selected scale of the pole ^[4] . There are several formal mathematical definitions.fractal dimension, which are built on this basic concept, about the change in the element with a change in scale.

One elementary example is the fractal dimension of a Koch snowflake . Its topological dimension is 1, but this is by no means a rectifiable curve , since the length of the curve between any two points of the Koch snowflake is infinity . No arbitrarily small part of the curve is a line segment. Rather, the Koch snowflake consists of an infinite number of segments connected at different angles. The fractal dimension of the curve can be explained intuitively, assuming that the fractal line is an object too detailed (detailed) to be one-dimensional, but not complex enough to be two-dimensional ^[5] . Therefore, its dimension is better described not by the usual topological dimension 1, but by its fractal dimension, which in this case is equal to the number lying in the interval between 1 and 2.

Content

1 Introduction
2 History
3 The role of scale
4 Dimension is not the only parameter
5 Examples
6 Evaluation of real data
7 See also
8 notes
9 notes
10 Literature
11 Further reading
12 Links

Introduction

Figure 2. 32 square segments form a fractal and are visible through a rectangular magnifier of different sizes. The pattern illustrates self-similarity . The theoretical fractal dimension for this fractal is T ^log32 ⁄ _log8 = 1.67. Its empirical fractal dimension from capacitive analysis is ± 1% ^[6] .

Fractal dimension is a coefficient that describes fractal structures or sets based on a quantitative assessment of their , as the coefficient of change in a part with a change in scale ^[4] . Some types of fractal dimension can be measured theoretically and ( see Fig. 2 ) ^[7] ^[8] . Fractal dimensions are used to characterize a wide range of objects from abstract ^[9] ^[7] to practical phenomena, for example: turbulence, ^[4] river networks urban growth, ^[10] human physiology, ^[11] ^[12] medicine ^[8] and market trends ^[13] . The basic idea of fractional or fractal dimension has a long history in mathematics, which can be traced back to 1600, ^[4] ^[14] but the terms fractal and fractal dimension were introduced by mathematician Benoit Mandelbrot in 1975 ^[9] ^[4] ^[8] ^[13] ^[15] .

Fractal dimension was first introduced as a coefficient describing geometrically complex forms, for which details are more important than the full figure ^[15] . For sets describing ordinary geometric shapes, the theoretical fractal dimension is equal to the usual Euclidean or topological dimension . Thus, for sets describing points, the theoretical fractal dimension is 0; 1 for sets describing a line (sets having only length); 2 for sets describing a surface (having length and width); 3 for sets describing the volume (sets having length, width and height). But this is changing for fractal sets. If the theoretical fractal dimension of a set exceeds the topological dimension, then it is believed that the set has fractal geometry ^[16] .

In contrast to the topological dimension, the fractal coefficient can take a non- integer value ^[17] , showing that the fractal set fills the space not as it is filled with the usual geometric set ^[9] ^[18] ^[7] . For example, a curve with a fractal dimension very close to 1, say 1.10, behaves quite like a normal line, but a curve with a fractal dimension of 1.9 is wound in space, almost like a surface. Similarly, a surface with a fractal dimension of 2.1 behaves. It fills the space almost like an ordinary surface, but a surface with a fractal dimension of 2.9 collapses and tends to fill the space almost like a volume ^[16] ^{[notes 1]} . This general connection can be seen in the 2 image of the fractal curve in see Fig. 2 and see Fig. 3 - 32 segments, the contour in Fig. 2 , entangled and filling the space. This fractal curve has a dimension of 1.67 compared to the less complex Koch curve in Fig. 3 , which has a fractal dimension of 1.26.

Figure 3. The Koch curve is a classic fractal curve. We take a single segment, divide it into three equal parts and replace the middle interval with an equilateral triangle without this segment. As a result, a polyline is formed, consisting of four links of length ¹ ⁄ ₃ . In the next step, repeat the operation for each of the four resulting links. The limit curve is the Koch curve

The relation between the increasing fractal dimension and the filling space can be taken as the fractal dimension of the measured density, but this is not so. These two parameters do not strictly correlate ^[6] . Instead, fractal dimension measures complexity. This concept is associated with certain features of fractals: self-similarity , pattern, and unevenness ^{[notes 2]} . These properties are found in the fractal curve examples described above. Both curves with a topological dimension equal to 1 so that it can be hoped that their length or angular coefficient can be measured, as with ordinary lines. But we cannot do any of these things, because fractal curves have complexity in the form of self-similarity and patterns, which is not the case with ordinary lines ^[4] . Self-similarity lies on an infinite scale, and the pattern in the defining elements of each set. The length between any two points of these curves is not defined , because theoretically these structures never stop, but repeat themselves an infinite number of times ^[19] . Each smaller part consists of an infinite number of scale segments that look exactly like in the first iteration. These are not rectifiable curves , that is, we cannot divide them into separate segments and calculate approximately the length. We cannot describe using length and angular coefficient. However, their fractal dimensions can be determined. They show how to fill the space more than ordinary lines, but less than the surface, it also allows you to compare them with each other.

Note that the two fractal curves described above show a type of self-similarity that exactly repeats the initial pattern, which is easy to visualize. Structures of this kind can also be found in other spaces (for example, ). If the Koch curve is expanded into 3-dimensional space, then its theoretical fractal dimension will be equal to 2.5849. However, there is a difficulty in calculating the fractal dimension for the following example ^[7] ^[13] : the UK coast is an approximate model with an approximate scale ^[4] . In general, fractals can be of different types, degrees of self-similarity, and patterns that are difficult to visualize. They include, as examples, strange attractors : smooth piles ^[16] , Julia set and heart rate ^[20] . Fractal complexity is not always easy to calculate without relying on complex analytical methods, which still lead to an answer through fractal dimensions ^[4] .

History

The terms fractal dimension and fractal were introduced by Mandelbrot in 1975 ^[15] , about 10 years after he published his article on self-similarity of the coast of Great Britain. Mandelbrot combined and applied complex theoretical mathematics and engineering work in a new version of the study of complex geometry. This challenged the usual linear terms ^[14] ^[21] ^[22] . The earliest roots that Mandelbrot summarized in the concept of “fractal geometry” were clearly traced in essays on the indifference, infinity of self-similar functions, which are important in the mathematical definition of fractals. Around the time, an analysis was published (in the mid-1600s) ^[4] . There was a break in the publication of papers on such functions. Beginning in the late 1800s with the creation of mathematical functions and sets, which today are called canonical fractals (such as the work of the same name by von Koch , ^[19] Sierpinski , Julia ), an update began in this area. At this time, their formulation was often considered as strongly contradicting mathematical "monsters" ^[14] ^[22] . These works were apparently accompanied by assumptions that they are the most crucial moment in the development of the concept of fractal geometry, through the works of Hausdorff in the early 1900s. Hausdorff defined the “fractional dimension”, which is now called by his name and is often used in the definition of modern fractals ^[3] ^[4] ^[16] ^[21] .

See the history of fractals in more detail .

The role of scale

Figure 4. A traditional view of geometry about defining scale and dimension.

The idea of fractal dimension lies in an unconventional representation of scale and dimension ^[23] . This can be seen in Fig. 4 , illustrating the traditional concepts of geometry, which form the scale predictably and according to understandable and familiar ideas about the space in which they are contained. For example, take a line, divide it into three equal parts, then each part will be 3 times shorter than the length of the original line. This also takes place in the plane. If you measure the area of the square, and then measure the area of the square with a side ¹ ⁄ ₃ long from the length of the side of the initial square, it will be 9 times smaller than the area of the initial square. This scale can be determined mathematically using the scale rule in Equation 1, where $N$ ${\ displaystyle N}$ - number of parts $\epsilon$ ${\ displaystyle \ epsilon}$ - scale factor, $D$ ${\ displaystyle D}$ - fractal dimension:

${N\propto \epsilon ^{-D}}$ ${\ displaystyle {N \ propto \ epsilon ^ {- D}}}$

(one)

Symbol $\propto$ ${\ displaystyle \ propto}$ means proportionality. This scale rule confirms the traditional scale geometry rules, because for a line - $N$ ${\ displaystyle N}$ = 3 when $\epsilon$ ${\ displaystyle \ epsilon}$ = ¹ ⁄ ₃ , then $D$ ${\ displaystyle D}$ = 1, and for squares, because $N$ ${\ displaystyle N}$ = 9 when $\epsilon$ ${\ displaystyle \ epsilon}$ = ¹ ⁄ ₃ , $D$ ${\ displaystyle D}$ = 2.

Figure 5. The first 4 iterations of the Koch Snowflake , which has an approximate Hausdorff dimension of 1.2619.

The same rule applies to fractal geometry, but less intuitively. To calculate a unit length for a fractal line, at first glance, we scale down 3 times, in this case $N$ ${\ displaystyle N}$ = 4 when $\epsilon$ ${\ displaystyle \ epsilon}$ = ¹ ⁄ ₃ and the value $D$ ${\ displaystyle D}$ can be found by transforming Equation 1:

${\log _{\epsilon }{N}={-D}={\frac {\log {N}}{\log {\epsilon }}}}$ ${\ displaystyle {\ log _ {\ epsilon} {N} = {- D} = {\ frac {\ log {N}} {\ log {\ epsilon}}}}}$

(2)

Thus, for the fractal described through $N$ ${\ displaystyle N}$ = 4 when $\epsilon$ ${\ displaystyle \ epsilon}$ = ¹ ⁄ ₃ , $D$ ${\ displaystyle D}$ = 1.2619. In this case, the dimension does not take an integer value, therefore, it can be assumed that the fractal has a dimension not equal to the dimension of the space into which it is embedded ^[7] . The same scale is used for the Koch Curve and the Koch snowflake . It should be noted that these images themselves are not true fractals, since scaling is described by the value $D$ ${\ displaystyle D}$ cannot continue indefinitely for the simple reason that images exist only at the smallest point - a pixel. The theoretical structure, which is a digital image, does not have discrete pixels, like pieces, but consists of an infinite number of segments at different angles with a fractal dimension equal to 1.2619 ^[4] ^[23] .

Dimension is not the only parameter.

Figure 6. Two L-systems, which at each iteration receive 4 parts of scale ¹ ⁄ ₃ times smaller than the previous iteration. They have the same fractal dimension as for the Koch curve ^[6] .

As in the case with the dimension defined for the line, square and cube, fractal dimensions are common characteristics, which does not allow us to uniquely determine the structure ^[23] ^[24] . Value $D$ ${\ displaystyle D}$ for the Koch fractal was given above, for example, the quantitative structure has a scale, but this is not enough to build it. Many fractal structures and patterns can be built at the same scale as the Koch curve, but they will still differ from the Koch curve ( see Figure 6 ).

Examples of fractals: see Fractal , Sierpinski Triangle , Mandelbrot Set , , .

Examples

Figure 7. A straight line of unit length is taken. Then it is divided into three equal parts, and the middle segment is taken out. In the second step of the similar procedure, the remaining segments are exposed. So the process continues to infinity.

The concept of fractal dimension described in this article is a classical view of a complex structure. The examples described here were selected for illustration purposes. The scale and ratio have been known for a long time. In practice, however, fractal dimensions can be determined using methods that take an approximate scale. As the definition of fractal dimension in the book of Bozhokin S. V. and Parshin D. A. "Fractals and multifractals" ^[2] use the following formula:

D=-\lim \limits _{\varepsilon \to 0}{\frac {\ln(N_{\varepsilon })}{\ln(\varepsilon )}}

{\ displaystyle D = - \ lim \ limits _ {\ varepsilon \ to 0} {\ frac {\ ln (N _ {\ varepsilon})} {\ ln (\ varepsilon)}}}

where

N_{\varepsilon }

{\ displaystyle N _ {\ varepsilon}}

- the minimum number of n-dimensional "balls" of radius

\varepsilon

{\ displaystyle \ varepsilon}

needed to cover the set.

According to this formula, for an isolated point, a length segment $L$ ${\ displaystyle L}$ surface area $S$ ${\ displaystyle S}$ volume spaces $V$ ${\ displaystyle V}$ fractal dimension coincides with the usual Euclidean dimension.

Using this formula, we can calculate the fractal dimension, for example, of the Cantor set ( see Figure 7 ). Obviously on $n$ ${\ displaystyle n}$ -th step we get $2^{n}$ ${\ displaystyle 2 ^ {n}}$ lengths ${\frac {1}{3^{n}}}$ ${\ displaystyle {\ frac {1} {3 ^ {n}}}}$ , which implies that the fractal dimension for the Cantor set is 0, 6309 ^[2] .

Several formal definitions of different types of fractal dimension are given below. Despite the fact that for some classical fractals all these dimensions coincide, in the general case they are not equivalent:

Minkowski dimension : D is estimated as an exponent of a power law.

D_{0}=\lim _{\epsilon \rightarrow 0}{\frac {\log N(\epsilon )}{\log {\frac {1}{\epsilon }}}}.

{\ displaystyle D_ {0} = \ lim _ {\ epsilon \ rightarrow 0} {\ frac {\ log N (\ epsilon)} {\ log {\ frac {1} {\ epsilon}}}}.

Information dimension: D is considered as the average information necessary to identify the occupied capacity with the size of this capacity; $p$ ${\ displaystyle p}$ - probability.

D_{1}=\lim _{\epsilon \rightarrow 0}{\frac {-\langle \log p_{\epsilon }\rangle }{\log {\frac {1}{\epsilon }}}}

{\ displaystyle D_ {1} = \ lim _ {\ epsilon \ rightarrow 0} {\ frac {- \ langle \ log p _ {\ epsilon} \ rangle} {\ log {\ frac {1} {\ epsilon}}} }}

D is based on $M$ ${\ displaystyle M}$ and g _ε , where $M$ ${\ displaystyle M}$ Is the number of points used to represent the fractal, g _ε is the number of pairs of points closer than ε to each other.

D_{2}=\lim _{\epsilon \rightarrow 0,M\rightarrow \infty }{\frac {\log(g_{\epsilon }/M^{2})}{\log \epsilon }}

{\ displaystyle D_ {2} = \ lim _ {\ epsilon \ rightarrow 0, M \ rightarrow \ infty} {\ frac {\ log (g _ {\ epsilon} / M ^ {2})} {\ log \ epsilon} }}

Generalized Renyi Dimensions

The Minkowski dimension, information and correlation dimensions can be considered as a special case of a continuous spectrum of generalized dimensions of the order of α, defined as follows:

D_{\alpha }=\lim _{\epsilon \rightarrow 0}{\frac {{\frac {1}{1-\alpha }}\log(\sum _{i}p_{i}^{\alpha })}{\log {\frac {1}{\epsilon }}}}

{\ displaystyle D _ {\ alpha} = \ lim _ {\ epsilon \ rightarrow 0} {\ frac {{\ frac {1} {1- \ alpha}} \ log (\ sum _ {i} p_ {i} ^ {\ alpha})} {\ log {\ frac {1} {\ epsilon}}}}}

Higuchi Dimension ^[25]

$D={\frac {d\ \log(L(k))}{d\ \log(k)}}$ ${\ displaystyle D = {\ frac {d \ \ log (L (k))} {d \ \ log (k)}}}$

Multifractal dimensions: a special case of Renyi Dimensions, when the behavior of the scale changes in different parts of the figure.
Hausdorff Dimension
Locally related dimension ^[26]

Real Data Evaluation

Many real-life phenomena show limited or statistical fractal properties and fractal dimensions that can be estimated from a data sample using a computer based on methods. In practice, measurements of fractal dimension depend on various methodological issues, and are sensitive to numerical or experimental noise and limited in the amount of data. Nevertheless, the region is developing rapidly in the estimation of fractal dimension for statistical self-similar phenomena. Fractal dimension has many practical applications in various fields, including diagnostic imaging, ^[27] ^[28] physiology, ^[11] neurobiology, ^[12] medicine, ^[29] ^[30] ^[31] physics, ^[32] ^[33] analysis images, ^[34] ^[35] ^[36] ^[37] acoustics, ^[38] zeros of the Riemann zeta function ^[39] and electrochemical processes ^[40] .

An alternative to direct measurement is a mathematical model that resembles the formation of a real fractal object. In this case, the verification can also be done by comparing other fractal properties arising from the model with the measurement data. In colloidal physics , systems are composed of particles with various fractal dimensions. To describe these systems, the probability distribution of fractal dimension is used. And in the end, time is the evolution of the latter: it is a process that is due to the complex interaction between and coalescence ^[41] .

Remarks

↑ See
↑ See Fractal Parameters

Notes

↑ Mandelbrot B., 2002 .
↑ ¹ ² ³ Bozhokin S.V., 2001 .
↑ ¹ ² Mandelbrot B., 1967 .
↑ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ ⁹ ¹⁰ ¹¹ Benoit B. Mandelbrot, 1983 .
↑ Harte D., 2001 .
↑ ¹ ² ³ Balay-Karperien A., 2004 .
↑ ¹ ² ³ ⁴ ⁵ Vicsek T. (1992), 1992 , p. 10.
↑ ¹ ² ³ Losa Gabriele A., Nonnenmacher Theo F., 2005 .
↑ ¹ ² ³ Falconer K., 2003 .
↑ Chen Y, 2011 .
↑ ¹ ² Popescu DP, 2010 .
↑ ¹ ² King RD, 2009 .
↑ ¹ ² ³ Peters E., 1996 .
↑ ¹ ² ³ Gerald E., 2004 .
↑ ¹ ² ³ Albers Alexanderson, Gerald L. Alexanderson, 2008 .
↑ ¹ ² ³ ⁴ Mandelbrot Benoit, 2004 .
↑ Sharifi-Viand A., Mahjani MG, Jafarian M., 2012 .
↑ Sagan H., 1994 .
↑ ¹ ² Helge von Koch, “On a continuous curve without tangents constructible from elementary geometry”, 2004 .
↑ Tan Can Ozan, Cohen Michael A., Eckberg Dwain L., Taylor J. Andrew, 2009 .
↑ ¹ ² Nigel G., 2000 .
↑ ¹ ² MacTutor History of Mathematics .
↑ ¹ ² ³ Iannaccone, Khokha, 1996 .
↑ Vicsek T. (2001), 2001 .
↑ Higuchi T ..
↑ Jelinek A., 2008 .
↑ Landini G., 1995 .
↑ Cheng Qiuming, 1997 .
↑ Liu Jing Z., 2003 .
↑ Smith TG, 1996 .
↑ Li J., 2009 .
↑ Dubuc B., 1989 .
↑ Roberts A., 1996 .
↑ Al-Kadi OS, 2008 .
↑ Pierre S., 1996 .
↑ Tolle CR, 2003 .
↑ Gorsich DJ, 1996 .
↑ Maragos P., 1999 .
↑ Shanker O., 2006 .
↑ Eftekhari A., 2004 .
↑ Kryven I., 2014 .

Literature

Al-Kadi OS, Watson D. Texture Analysis of Aggressive and non-Aggressive Lung Tumor CE CT Images // IEEE Transactions on Biomedical Engineering. - 2008. - T. 55 , No. 7 . - S. 1822-1830 . - DOI : 10.1109 / tbme.2008.919735 .
Alexanderson Albers, Alexanderson Gerald L. Benoit Mandelbrot: In his own words // Mathematical people: profiles and interviews. - Wellesley, Mass: AK Peters, 2008 .-- 214 p. - ISBN 978-1-56881-340-0 .
Balay-Karperien A. Defining Microglial Morphology: Form, Function, and Fractal Dimension . - Charles Sturt University, 2004 .-- P. 3 .-- 86 p.
Bozhokin S.V., Parshin D.A. Fractals and multifractals. - 2001 .-- S. 15-18. - 128 p. - ISBN 5-93972-060-9 .
Chen Y. Modeling Fractal Structure of City-Size Distributions Using Correlation Functions // PLoS ONE. - 2011. - T. 6 , No. 9 . - S. e24791 . - DOI : 10.1371 / journal.pone.0024791 . - . - arXiv : 1104.4682 . - PMID 21949753 .
Cheng Qiuming. Multifractal Modeling and Lacunarity Analysis // Mathematical Geology. - 1997. - T. 29 , No. 7 . - S. 919-932 . - DOI : 10.1023 / A: 1022355723781 . - PMID 7499097 .
Dubuc B., Quiniou J., Roques-Carmes C., Tricot C., Zucker S. Evaluating the fractal dimension of profiles // Physical Review A. - 1989. - Vol. 39 , No. 3 . - S. 1500-1512 . - DOI : 10.1103 / PhysRevA.39.1500 . - . - PMID 9901387 .
Eftekhari A. Fractal Dimension of Electrochemical Reactions // Journal of the Electrochemical Society. - 2004. - T. 151 , No. 9 . - S. E291 – E296 . - DOI : 10.1149 / 1.1773583 .
Falconer K. Fractal Geometry. - New York: Wiley, 2003 .-- 308 p. - P. 27–37. - ISBN 978-0-470-84862-3 .
Gerald E. Classics on Fractals. - Boulder: Westview Press, 2004. - P. 25–46. - 86 p. - ISBN 978-0-8133-4153-8 .
Gerald Edgar. Helge von Koch, “On a continuous curve without tangents constructible from elementary geometry” // Classics on Fractals. - Boulder: Westview Press, 2004. - P. 25–46. - ISBN 978-0-8133-4153-8 .
Gorsich DJ, Tolle CR, Karlsen RE, Gerhart GR Wavelet Applications in Signal and Image Processing IV // IEEE Transactions on Pattern Analysis and Machine Intelligence. - 1996.- T. 2825 . - S. 109 . - DOI : 10.1117 / 12.255224 .
Harte D. Multifractals. - London: Chapman & Hall, 2001 .-- P. 3-4. - ISBN 978-1-58488-154-4 .
Higuchi T. Approach to an irregular time series on the basis of the fractal theory (neopr.) (Unavailable link) (1987). Date of treatment January 16, 2016. Archived March 4, 2016.
Iannaccone, Khokha. Fractal Geometry in Biological Systems. - 1996. - ISBN 978-0-8493-7636-8 .
Jelinek A., Jelinek HF, Leandro JJ, Soares JV, Cesar Jr RM, Luckie A. Automated detection of proliferative retinopathy in clinical practice // Journal of Electroanalytical Chemistry. - 2008. - T. 2 , No. 1 . - S. 109–122 . - DOI : 10.2147 / OPTH.S1579 . - PMID 19668394 .
King RD Characterization of Atrophic Changes in the Cerebral Cortex Using Fractal Dimensional Analysis // Brain Imaging and Behavior. - 2009. - T. 3 , No. 2 . - S. 154–166 . - DOI : 10.1007 / s11682-008-9057-9 . - PMID 20740072 .
Kryven I., Lazzari S., Storti G. Population Balance Modeling of Aggregation and Coalescence in Colloidal Systems // Macromolecular Theory and Simulations. - 2014. - T. 23 , No. 3 . - S. 170 . - DOI : 10.1002 / mats.201300140 .
Landini G., Murray PI, Misson GP Local connected fractal dimensions and lacunarity analyses of 60 degrees fluorescein angiograms // Investigative Ophthalmology & Visual Science. - 1995. - T. 36 , No. 13 . - S. 2749-2755 . - PMID 7499097 .
Li J., Du Q., Sun C. An improved box-counting method for image fractal dimension estimation // Pattern Recognition. - 2009. - T. 42 , No. 11 . - S. 2460 . - DOI : 10.1016 / j.patcog.2009.03.03.001 . - . - PMID 8946315 .
Liu Jing Z., Zhang Lu D., Yue Guang H. Fractal Dimension in Human Cerebellum Measured by Magnetic Resonance Imaging // Biophysical Journal. - 2003. - T. 85 , No. 6 . - S. 4041–4046 . - DOI : 10.1016 / S0006-3495 (03) 74817-6 . - . - PMID 14645092 .
Losa Gabriele A., Nonnenmacher Theo F. Fractals in biology and medicine . - Springer, 2005. - ISBN 978-3-7643-7172-2 .
Mandelbrot B. How Long is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension // Science. - 1967. - T. 156 , No. 3775 . - S. 636-638 . - DOI : 10.1126 / science.156.3775.636 . - . - PMID 17837158 .
Mandelbrot Benoit B. The fractal geometry of nature . - Macmillan, 1983. - ISBN 978-0-7167-1186-5 .
Mandelbrot B. Fractal geometry of nature. - 2002. - S. 46. - 666 p.
Mandelbrot Benoit. Fractals and Chaos. - Berlin: Springer, 2004 .-- P. 38. - ISBN 978-0-387-20158-0 .
Maragos P., Potamianos A. Fractal dimensions of speech sounds: Computation and application to automatic speech recognition // The Journal of the Acoustical Society of America. - 1999. - T. 105 , No. 3 . - S. 1925-1932 . - DOI : 10.1121 / 1.426738 . - . - PMID 10089613 .
Nigel G. Introducing fractal geometry. - Duxford: Icon, 2000. - P. 71. - ISBN 978-1-84046-123-7 .
Peters E. Chaos and order in the capital markets: a new view of cycles, prices, and market volatility. - New York: Wiley, 1996 .-- ISBN 0-471-13938-6 .
Pierre S., Jean-F. Ivest On the Validity of Fractal Dimension Measurements in Image Analysis // Journal of Visual Communication and Image Representation. - 1996. - T. 7 , No. 3 . - S. 217-229 . - ISSN 1047-3203 . - DOI : 10.1006 / jvci.1996.0020 . Archived July 20, 2011.
Popescu, DP, Flueraru, C., Mao, Y., Chang, S., Sowa, MG Signal attenuation and box-counting fractal analysis of optical coherence tomography images of arterial tissue // Biomedical Optics Express. - 2010. - T. 1 , No. 1 . - S. 268–277 . - DOI : 10.1364 / boe.1.000268 . - PMID 21258464 .
Roberts A., Cronin A. Unbiased estimation of multi-fractal dimensions of finite data sets // Physica A: Statistical Mechanics and its Applications. - 1996. - T. 233 , No. 3-4 . - S. 867 . - DOI : 10.1016 / S0378-4371 (96) 00165-3 . - .
Sagan H. Space-Filling Curves. - Berlin: Springer-Verlag, 1994 .-- 156 p. - ISBN 0-387-94265-3 .
Shanker O. Random matrices, generalized zeta functions and self-similarity of zero distributions // Journal of Physics A: Mathematical and General. - 2006. - T. 39 , No. 45 . - S. 13983 . - DOI : 10.1088 / 0305-4470 / 39/45/008 . - .
Sharifi-Viand A., Mahjani MG, Jafarian M. Investigation of anomalous diffusion and multifractal dimensions in polypyrrole film // Journal of Electroanalytical Chemistry. - 2012 .-- T. 671 . - S. 51 . - DOI : 10.1016 / j.jelechem.2012.02.014 .
Smith TG, Lange GD, Marks WB Fractal methods and results in cellular morphology - dimensions, lacunarity and multifractals // Journal of Neuroscience Methods. - 1996. - T. 69 , No. 2 . - S. 123–136 . - DOI : 10.1016 / S0165-0270 (96) 00080-5 . - . - PMID 8946315 .
Tan Can Ozan, Cohen Michael A., Eckberg Dwain L., Taylor J. Andrew. Fractal properties of human heart period variability: Physiological and methodological implications // Journal of Electroanalytical Chemistry. - 2009. - T. 587 , No. 15 . - S. 3929 . - DOI : 10.1113 / jphysiol.2009.169219 .
Tolle CR, McJunkin TR, Gorsich DJ Suboptimal minimum cluster volume cover-based method for measuring fractal dimension // IEEE Transactions on Pattern Analysis and Machine Intelligence. - 2003 .-- T. 25 . - S. 32 . - DOI : 10.1109 / TPAMI.2003.1159944 . Archived July 20, 2011.
Trochet, Holly. A History of Fractal Geometry (Neopr.) . MacTutor History of Mathematics (2009). Archived February 4, 2012.
Vicsek T. Fractal growth phenomena. - Singapore New Jersey: World Scientific, 1992 .-- 165 p. - ISBN 5-09-002630-0 .
Vicsek T. Fluctuations and scaling in biology. - Oxford [Oxfordshire]: Oxford University Press, 2001. - ISBN 0-19-850790-9 .

Links

TruSoft's Benoit , fractal analysis software product calculates fractal dimensions and hurst exponents.
A Java Applet to Compute Fractal Dimensions
Introduction to Fractal Analysis
Bowley, Roger Fractal Dimension (Neopr.) . Sixty Symbols . Brady Haran for the University of Nottingham (2009).

[19] See

[20] See Fractal Parameters

[_fb42aaa0520d00e5-1] Mandelbrot B., 2002 .

[_c2a882f1f2a11f3d-2] ¹ ² ³ Bozhokin S.V., 2001 .

[_3c608af269674e92-3] ¹ ² Mandelbrot B., 1967 .

[_ecf7a4b04bea9b85-4] ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ ⁹ ¹⁰ ¹¹ Benoit B. Mandelbrot, 1983 .

[_cd17b46739e37194-5] Harte D., 2001 .

[_5d1779d9465b6328-6] ¹ ² ³ Balay-Karperien A., 2004 .

[_c8cbb36679ce6824-7] ¹ ² ³ ⁴ ⁵ Vicsek T. (1992), 1992 , p. 10.

[_6e0788aa1255d0c1-8] ¹ ² ³ Losa Gabriele A., Nonnenmacher Theo F., 2005 .

[_1447e1343a46ccc5-9] ¹ ² ³ Falconer K., 2003 .

[_975a4f135d6e95a2-10] Chen Y, 2011 .

[_7bef59358111f165-11] ¹ ² Popescu DP, 2010 .

[_3acaaf8b23565b83-12] ¹ ² King RD, 2009 .

[_b795cf65429baed2-13] ¹ ² ³ Peters E., 1996 .

[_bad84d31ce91bf0d-14] ¹ ² ³ Gerald E., 2004 .

[_4888f1637b04af37-15] ¹ ² ³ Albers Alexanderson, Gerald L. Alexanderson, 2008 .

[_29738d3687d1786c-16] ¹ ² ³ ⁴ Mandelbrot Benoit, 2004 .

[_efc2852f0ff88abc-17] Sharifi-Viand A., Mahjani MG, Jafarian M., 2012 .

[_1621b387ac8a3c60-18] Sagan H., 1994 .

[_0eed95e488dd1147-21] ¹ ² Helge von Koch, “On a continuous curve without tangents constructible from elementary geometry”, 2004 .

[_ea7784310bc5cbe0-22] Tan Can Ozan, Cohen Michael A., Eckberg Dwain L., Taylor J. Andrew, 2009 .

[_4ac5506db013655b-23] ¹ ² Nigel G., 2000 .

[_25a1a8911c85781f-24] ¹ ² MacTutor History of Mathematics .

[_2154981a2accb715-25] ¹ ² ³ Iannaccone, Khokha, 1996 .

[_d76883ec625d59e7-26] Vicsek T. (2001), 2001 .

[_700de01e79a9f0ba-27] Higuchi T ..

[_62ce62e6f6661ee8-28] Jelinek A., 2008 .

[_e1159dcb4ab59dbb-29] Landini G., 1995 .

[_9f02bb411f3e7f84-30] Cheng Qiuming, 1997 .

[_21456af68d67678e-31] Liu Jing Z., 2003 .

[_c183370da17f7700-32] Smith TG, 1996 .

[_41a874d2f54d47f1-33] Li J., 2009 .

[_5736a92f648adebb-34] Dubuc B., 1989 .

[_315ac4f6932ba932-35] Roberts A., 1996 .

[_b8368893aca5fa92-36] Al-Kadi OS, 2008 .

[_d8f4314c0846e36a-37] Pierre S., 1996 .

[_8409d6e00b2e9c19-38] Tolle CR, 2003 .

[_f998e4bf995c59f5-39] Gorsich DJ, 1996 .

[_365a9cfcd8009945-40] Maragos P., 1999 .

[_52046e9c797f5e02-41] Shanker O., 2006 .

[_4d558d65c06da375-42] Eftekhari A., 2004 .

[_09eb7c56f23b2092-43] Kryven I., 2014 .