Node (math)

Eight (Listing node)

A knot in mathematics is an embedding of a circle (a two-dimensional sphere) in a three - dimensional Euclidean space , considered up to isotopy . The main subject of the study of knot theory . Two nodes are topologically equivalent if one of them can be deformed into the other, and self-intersections should not occur in the process of deformation.

A special case is the question of recognizing the triviality of a particular knot, that is, whether a given knot is isotopic to a trivial knot (can it be decoupled).

To determine whether a particular knot is trivial, one can use various knot invariants , for example, the Alexander polynomial or the fundamental complement group . Usually they can be calculated based on the nodal diagram .

Content

1 Classification
2 Knots and gears
3 Invariants of knots
4 Node Addition
5 notes
6 Literature

Classification

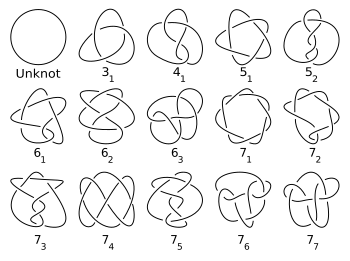
Trefoil knot $3_{1}$ ${\ displaystyle 3_ {1}}$ is the first nontrivial knot and the only node with three intersections . It is simple and is listed with number 3 ₁ in the Alexander-Briggs notation . for trefoil is 4 6 2, and Conway's trefoil notation is [3].

The trefoil is nontrivial, which means that it is impossible to “untie” the trefoil in three-dimensional space without cutting. From a mathematical point of view, this means that the trefoil is not isotopic to the trivial knot . In particular, there is no sequence of Reidemeister moves by which the knot is untied.

Eight , four-fold knot or Listing knot, knot $4_{1}$ ${\ displaystyle 4_ {1}}$ - one of the simplest non-trivial nodes. The eight is indicated by $4_{1}$ ${\ displaystyle 4_ {1}}$ . First reviewed by Listing , a student of Gauss, in 1847 .

The trefoil is chiral in the sense that the trefoil is different from its own specular reflection. Two shamrocks are known as left-handed and right-handed. It is impossible to deform the left-sided variant by continuous deformation into the right-sided one or vice versa. (That is, these two shamrocks are not isotopic.)

Also, it can be shown that the trefoil (both right and left) is not isotopic to the eight.

The quintuple , also known as the knot $5_{1}$ ${\ displaystyle 5_ {1}}$ in the designations of Alexander and Briggs, the “Cinquefoil” knot and the seal of Solomon is a knot for which the number of intersections (the minimum possible number of self-intersections in the diagram — a flat figure — of the knot) is five.

For multicomponent nodes, the number of components is indicated in the upper index: for example, the engagement of two rings has a symbolic notation $2_{1}^{2}$ ${\ displaystyle 2_ {1} ^ {2}}$ .

These were examples of polynomial ^[1] nodes. The non-polynomial knot is a wild knot ^[2]

An example of a wild knot.

Wild Knot - Knot $L$ ${\ displaystyle L}$ in Euclidean space $E^{3}$ ${\ displaystyle E ^ {3}}$ such that there is no homeomorphism $E^{3}$ ${\ displaystyle E ^ {3}}$ on yourself, in which $L$ ${\ displaystyle L}$ goes into a closed polyline, consisting of a finite number of segments.

Knots and gears

An investment (more often - its image) of a disconnected sum $\mu$ ${\ displaystyle \ mu}$ circle instances in $\mathbb {R} ^{3}$ ${\ displaystyle \ mathbb {R} ^ {3}}$ or $S^{3}$ ${\ displaystyle S ^ {3}}$ called a meshing of multiplicity $\mu$ ${\ displaystyle \ mu}$ .

Meshing multiplicity $\mu =1$ ${\ displaystyle \ mu = 1}$ called a node .

The nodes that make up this mesh are called its components .

Invariants of nodes

In knot theory, the number of intersections of a node is the smallest number of intersections on any diagram of a node. The number of intersections is a knot invariant .

For example, a trivial knot has zero intersections, the number of trefoil intersections is three, and the number of eight intersections is four.

Node

Play media file

6₂ Knot

asserts that the as a topological space ] is a “complete invariant” of a node, in the sense that it distinguishes a given node from all the others up to an ambient isotopy and mirror reflection . Among the invariants associated with the complement of a node, there is a group of a node , which is simply a fundamental group of its complement.

Notes

↑ Armstrong (1983 ), p. 215.
↑ Livingstone (1996 ), Section 2.1 Wild Knots and Unknottings, pp. 11-14.

Literature

Simon Jonathan. Mathematical Approaches to Biomolecular Structure and Dynamics / Jill P. Mesirov, Klaus Schulten, De Witt Sumners. - 1996. - T. 82. - (The IMA Volumes in Mathematics and its Applications). - DOI : 10.1007 / 978-1-4612-4066-2_4 .
PG Tait. Scientific papers. - Cambridge University Press, 1898 .-- T. 1.
CA Adams. The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. - American Mathematical Society, 2004. - ISBN 9780821836781 .
Crowell R., Fox R. Introduction to knot theory / Transl. from English - Cherepovets: Mercury Press, 2000 .-- 348 p. - ISBN 5-1148-0112-0 . .
Manturov V.O. Knot Theory. - M .: RHD, 2005 .-- 512 s. - ISBN 5-93972-404-3 . .
Manturov V.O. Lectures on the theory of knots and their invariants. - M .: URSS editorial, 2001 .-- 204 p. - ISBN 5-8360-0287-8 . .
Milnor J. Singular points of complex hypersurfaces / Per. from English - M .: Mir, 1971. - 127 p.
Mandelbaum R. Four-dimensional topology / Per. from English - M .: Mir, 1981. - 286 p.
Hillman JA Alexander ideals of links B. - Hdlb. - NY, 1981.
Jones, Vaughan F.R. Knot Theory and Statistical Mechanics // Scientific American (Russian edition). - No. 1. - 1991. - S. 44-50.
Sosinsky, A. B. Knots and braids . - M .: ICMMO , 2001 .-- T. 10 .-- 24 p. - (Library "Mathematical Education"). - ISBN 5-900916-76-6 . .
Articles "Theory of knots at the end of the XX century" // Mathematical education . - No. 3. - 1999.
Manturov V.O. Excursion into the theory of knots // Network educational journal . - 2004. - T. 8 , No. 1 . - S. 122-127 .
H. Gruber. Estimates for the minimal crossing number. - 2003 .-- arXiv : math / 0303273 .
Yuanan Diao. The additivity of crossing numbers // Journal of Knot Theory and its Ramifications. - 2004. - T. 13 , no. 7 . - DOI : 10.1142 / S0218216504003524 .
Marc Lackenby. The crossing number of composite knots // Journal of Topology. - 2009. - T. 2 , no. 4 . - DOI : 10.1112 / jtopol / jtp028 .
Honda K. 3-dimensional methods in contact geometry . (eng.)
Etnyre JB Legendrian and Transversal Knots . (eng.)
Birman JS Braids, knots and contact structures . (eng.)
Weisstein, Eric W. Knot Theory ( Wolfram ) at Wolfram MathWorld .

[Armstrong-1] Armstrong (1983 ), p. 215.

[wild-2] Livingstone (1996 ), Section 2.1 Wild Knots and Unknottings, pp. 11-14.