Gold spiral

The Durer spiral and the golden spiral, inscribed in a sequence of golden rectangles nested into each other: the green spiral - the Durer spiral - is made up of quarters of circles inside the squares, while the red spiral is a golden spiral, a special kind of logarithmic spiral . Overlapping sections are shown in yellow . The length of the spiral inside the larger square is the length of the spiral inside the next square in the golden ratio

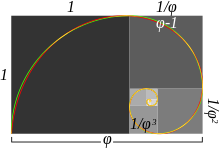
The golden spiral or the Fibonacci spiral is a logarithmic spiral whose growth coefficient is φ ⁴ , where φ is the golden ratio . The growth coefficient of the logarithmic spiral shows how many times the polar radius of the spiral has changed when rotated through an angle of 360 °. ^[1] This spiral got its name because of the connection with the sequence of rectangles nested into each other with the aspect ratio equal to φ , which are commonly called gold . The golden spiral can be entered into the system of such rectangles, and described around it. The gold spiral gained popularity due to the fact that the spiral known from the beginning of the 16th century and used in art ^[2] , built according to Dürer's method ^[3] ^[4] , turned out to be a good approximation for the golden spiral (see figure)

Content

Formula

The Fibonacci helix approximates the golden helix using quarter-circles in squares with squares equal to Fibonacci numbers. The figure shows the squares with the sizes 1, 1, 2, 3, 5, 8, 13, 21.

The equation for the gold spiral in the polar coordinate system is the same as for other logarithmic spirals , but with a special value of the growth factor - φ ⁴ :

r=a\varphi ^{\pm {\frac {2\theta }{\pi }}}

{\ displaystyle r = a \ varphi ^ {\ pm {\ frac {2 \ theta} {\ pi}}}}

,

where a is an arbitrary positive real constant, and $\varphi ={\frac {{\sqrt {5}}+1}{2}}$ ${\ displaystyle \ varphi = {\ frac {{\ sqrt {5}} + 1} {2}}}$ - the golden ratio .

The main property of the logarithmic spiral: the angle between the radius vector emanating from the pole and the tangent to the spiral - μ - is constant, and for the golden spiral is determined by the formula:

\operatorname {tg} \mu ={\dfrac {r}{r'}}={\dfrac {\pi }{2\ln \varphi }}

{\ displaystyle \ operatorname {tg} \ mu = {\ dfrac {r} {r '}} = {\ dfrac {\ pi} {2 \ ln \ varphi}}}

where

r'={\dfrac {dr}{d\theta }}

{\ displaystyle r '= {\ dfrac {dr} {d \ theta}}}

.

From where $\mu \approx 73^{\circ }$ ${\ displaystyle \ mu \ approx 73 ^ {\ circ}}$ .

Gold Spiral Approaches

Lithuanian coin

There are several similar spirals, which are close, but do not coincide exactly with the golden spiral ^[5] , with which they are often confused.

As it was already written above, when inscribing a golden spiral into a sequence of golden rectangles nested in each other, it is approximated by a spiral constructed according to the Dürer method. The golden rectangle can be divided into a square and a similar rectangle, it, in turn, is divided in the same way, and the process can be continued an arbitrary number of times. If interconnected quarters of circles are inscribed in these squares, the result is a spiral shown in the first figure.

Another approximation is the Fibonacci Spiral , which is constructed like the spiral described above, except that it starts from a rectangle of two squares and then adds a square of the same length to the larger side of the rectangle. As the relationship between adjacent Fibonacci numbers tends to the golden ratio, the spiral is increasingly approaching the golden spiral as we add squares (see the second figure).

Spirals in Nature

In nature, there are approximations to logarithmic spirals with a growth factor equal to φ ^k . For example, the shells of Nautilus pompilius mollusks and petrified ammonites are well described with k = 2, and the shells of some snails with k = 1. ^[6] The ratio of the lengths of three coils of the human ear coil is φ ^[7] , which corresponds to the helix with k = 1. Sleeves spiral galaxies , despite the existing assertions ^[8] , if they are described by a logarithmic, then they are not a golden spiral. In this case, the description it is a manifestation of random proximity. A recent analysis of the spirals found in the corneal epithelium of mice showed that both gold and other logarithmic spirals are found there. ^[9]

Notes

↑ Vygodsky M. Ya. Handbook of higher mathematics. M .: Science, 1977, p. 884.
↑ Prokhorov A. Golden Spiral, Quantum, 1984, №9.
↑ Arakelyan. G. Mathematics and the history of the golden section, M .: Logos, 2014, p. 50.
↑ Albrecht Durer (1525): Unterweysung der Messung mit dem Zirkel und Richtscheyt, in Linien Ebnen und gantzen Corporen. Verlag Dr. Alfons Uhl (Reprint 2000), Nordlingen, ISBN 3 921503 65 5 (Engl. Transl .: The Painter's Manual, Abaris Books, New York 1977).
↑ Madden, 1999 , p. 14–16.
↑ A.N. Kovalev, Once again about the golden spirals // Academy of Trinitarianism, M., El. No. 77-6567, publ.23545, 07.13.2017 http://www.trinitas.ru/rus/doc/0016/001f/3352-kv. pdf
↑ Petukhov S. V. Matrix genetics, genetic code algebras, noise immunity. - Moscow: Regular and chaotic dynamics, 2008. - p. 107.
↑ Gazale, 1999 , p. 3
↑ Rhee, 2015 , p. 22–38.

Literature

David Darling. The Universal Book of Mathematics: From Abracadabra to Zeno's Paradoxes. - John Wiley & Sons, 2004. - ISBN 9780471270478 .
Ivars Peterson. Sea Shell Spirals. - Society for Science & the Public, 2005-04-01.
Keith Devlin. The myth that will not go away. - May 2007.
Jerry Rhee, Talisa Mohammad Nejad, Olivier Comets, Sean Flannery, Eine Begum Gulsoy, Philip Iannaccone, Craig Foster. Promoting convergence: The Phi spiral in abduction of mouse corneal behaviors // Complexity. - 2015. - V. 20 , no. 3 - pp . 22–38 . - DOI : 10.1002 / cplx.21562 .
Midhat Gazale. Gnomon: From Pharaohs to Fractals. - Princeton University Press, 1999. - ISBN 9780691005140 .
Charles B. Madden. Fractals in Music: introductory mathematics for musical analysis. - High Art Press, 1999. - ISBN 0-9671727-6-4 .
Klaus Mainzer. Symmetries of Nature: A Handbook for Philosophy of Nature and Science. - Walter de Gruyter, 1996. - ISBN 3-11-012990-6 .
Priya Hemenway. Divine Proportion: Phi in Art, Nature, and Science. - Sterling Publishing Co, 2005. - ISBN 1-4027-3522-7 .

[1] Vygodsky M. Ya. Handbook of higher mathematics. M .: Science, 1977, p. 884.

[2] Prokhorov A. Golden Spiral, Quantum, 1984, №9.

[3] Arakelyan. G. Mathematics and the history of the golden section, M .: Logos, 2014, p. 50.

[4] Albrecht Durer (1525): Unterweysung der Messung mit dem Zirkel und Richtscheyt, in Linien Ebnen und gantzen Corporen. Verlag Dr. Alfons Uhl (Reprint 2000), Nordlingen, ISBN 3 921503 65 5 (Engl. Transl .: The Painter's Manual, Abaris Books, New York 1977).

[_b1b9fdffcbfef5dd-5] Madden, 1999 , p. 14–16.

[6] A.N. Kovalev, Once again about the golden spirals // Academy of Trinitarianism, M., El. No. 77-6567, publ.23545, 07.13.2017 http://www.trinitas.ru/rus/doc/0016/001f/3352-kv. pdf

[7] Petukhov S. V. Matrix genetics, genetic code algebras, noise immunity. - Moscow: Regular and chaotic dynamics, 2008. - p. 107.

[_b50718d2e1da7262-8] Gazale, 1999 , p. 3

[_804658cd60744bf3-9] Rhee, 2015 , p. 22–38.