Edge coloring

Ribbed 3-color coloring of Count Desargues .

Edge coloring - the assignment of "colors" to the edges of the graph so that no two adjacent edges have the same color. Edge coloring is one type of different type of coloring of graphs. The edge coloring problem asks whether it is possible to color the edges of a given graph at most $k$ ${\ displaystyle k}$ $k$ different colors for a given value $k$ ${\ displaystyle k}$ $k$ or for the smallest possible number of colors. The minimum required number of colors for coloring the edges of a given graph is called the chromatic index of the graph. For example, the edges of a graph in an illustration can be colored in three colors, but not in two, so the graph has a chromatic index of 3.

By Vizing's theorem, the number of colors needed for the edge coloring of a simple graph, or equal to the maximum degree of vertices $\Delta$ ${\ displaystyle \ Delta}$ $\ Delta$ either $\Delta +1$ ${\ displaystyle \ Delta +1}$ $\ Delta +1$ . For some graphs, such as bipartite graphs and high degree planar graphs , the number of colors is always equal $\Delta$ ${\ displaystyle \ Delta}$ $\ Delta$ , and for multigraphs the number of colors can be up to $3{\Delta }/2$ ${\ displaystyle 3 {\ Delta} / 2}$ $3 {\ Delta} / 2$ . There are polynomial time algorithms that create optimal coloring of bipartite graphs and coloring a simple non-bipartite graph with the number of colors ${\Delta }+1$ ${\ displaystyle {\ Delta} +1}$ ${\ Delta} +1$ . However, in the general case, the task of finding the optimal edge coloring is NP-complete and the fastest known algorithm for it works in exponential time. We studied many variations of the edge coloring problem, in which the conditions for assigning color to the edge must satisfy other conditions, rather than contiguity. Rib coloring tasks have applications in schedule tasks and in frequency assignment in fiber networks.

Examples

The graph-cycle can be painted in 2 colors if the length of the cycle is even - we just use 2 colors in succession passing through the edges of the cycle. However, in the case of an odd length, 3 colors are required ^[1] .

Geometric construction of coloring a complete graph.

K_{8}

{\ displaystyle K_ {8}}

in 7 colors. Each of the seven color classes has one edge connecting the center and one of the vertices of the polygon, and three edges perpendicular to it.

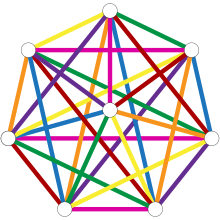
Full graph edges $K_{n}$ ${\ displaystyle K_ {n}}$ $K_n$ with $n$ ${\ displaystyle n}$ $n$ vertices can be painted $n-1$ ${\ displaystyle n-1}$ $n-1$ flowers if $n$ ${\ displaystyle n}$ $n$ evenly. This is a special case of Baraniai theorem . Soifer ^[2] gives the following geometric construction of the coloring in this case: $n$ ${\ displaystyle n}$ $n$ points in the corners and in the center of the correct $(n-1)$ {\ displaystyle (n-1)} $(n-1)$ -gon. For each color class, we select one edge connecting the center and one of the vertices of the polygon, and all the edges perpendicular to it, connecting the pairs of vertices of the polygon. However, if $n$ ${\ displaystyle n}$ odd required $n$ ${\ displaystyle n}$ colors - each color can only be used for coloring $(n-1)/2$ ${\ displaystyle (n-1) / 2}$ ribs $1/n$ ${\ displaystyle 1 / n}$ th part of all edges ^[3] .

Some authors have studied the edge coloring of odd graphs , $n$ ${\ displaystyle n}$ -regular graphs in which vertices represent teams from $(n-1)$ ${\ displaystyle (n-1)}$ players from the total $2n-1$ ${\ displaystyle 2n-1}$ players, and in which the edges represent possible pairs of these teams (with one player “offside” for refereeing). In the case when $n=3$ ${\ displaystyle n = 3}$ we get the well-known Count of Petersen . As explained by Bigs ^[4] , the problem (for $n=6$ ${\ displaystyle n = 6}$ ) consists in the fact that the players want to find such a schedule that the teams play each of the six games on different days of the week, excluding Sunday for all players. In a mathematical formulation, they want to find a 6-color edge coloring of 6-regular graphs $O_{6}$ ${\ displaystyle O_ {6}}$ . When $n$ ${\ displaystyle n}$ equals 3, 4 or 8, edge coloring of the graph $O_{n}$ ${\ displaystyle O_ {n}}$ requires $n+1$ ${\ displaystyle n + 1}$ colors, but for 5, 6 and 7 you only need $n$ ${\ displaystyle n}$ colors ^[5] .

Definitions

As in the case of vertex coloring , the edge coloring of the graph, unless otherwise specified, always assumes that two adjacent edges are assigned different colors. Two edges are considered adjacent if they have a common vertex. Count edge coloring $G$ ${\ displaystyle G}$ can be considered as the equivalent of vertex coloring of edge graphs $L(G)$ ${\ displaystyle L (G)}$ , a graph having a vertex for each edge of the graph $G$ ${\ displaystyle G}$ and edge for each pair of adjacent edges $G$ ${\ displaystyle G}$ .

Right coloring $k$ ${\ displaystyle k}$ different colors is called the (right) edge $k$ ${\ displaystyle k}$ coloring book. If for a graph one can find the (regular) edge $k$ ${\ displaystyle k}$ -coloring, they say that it is ribbed $k$ ${\ displaystyle k}$ -colored. The smallest number of colors needed for (correct) edge coloring of a graph $G$ ${\ displaystyle G}$ called the chromatic index , or edge chromatic number $\chi {\prime }(G)$ ${\ displaystyle \ chi {\ prime} (G)}$ . The chromatic index is sometimes written as $\chi _{1}(G)$ ${\ displaystyle \ chi _ {1} (G)}$ . In this notation, the index indicates that edges are one-dimensional objects. Count is edge $k$ ${\ displaystyle k}$ -color if the chromatic index is exactly equal $k$ ${\ displaystyle k}$ . Chromatic index should not be confused with chromatic number $\chi (G)$ ${\ displaystyle \ chi (G)}$ or $\chi _{0}(G)$ ${\ displaystyle \ chi _ {0} (G)}$ , the minimum number of colors necessary for the correct coloring of the vertices of the graph $G$ ${\ displaystyle G}$ .

Unless otherwise stated, all graphs are assumed to be simple, as opposed to multigraphs in which two or more edges can connect the same pair of vertices and in which there can be loops (an edge with finite vertices coinciding). For most edge coloring problems, simple graphs behave differently from multigraphs, and extra care is required when extending edge coloring theorems from simple graphs to multigraphs.

Matching Relationships

This 3-regular Planar graph has 16 vertices and 24 edges, but only 7 at any maximum matching. Thus, four colors are required for any edge coloring.

Match in column $G$ ${\ displaystyle G}$ called the set of edges, none of which are adjacent. A matching is called perfect if its edges contain all the vertices of the graph and maximum if it contains the maximum possible number of edges. In the edge coloring, the edges of the same color must be non-adjacent, so that they form a matching. Thus, a regular edge coloring is the same as decomposing a graph into disjoint matching.

If the size of the maximum matching in the given graph is small, a large number of matching is necessary to cover all the edges of the graph. More formal, this explanation assumes that if a graph has $m$ ${\ displaystyle m}$ edges and if maximum $\beta$ ${\ displaystyle \ beta}$ edges can belong to the maximum matching, then each edge coloring of the graph must contain at least $m/\beta$ ${\ displaystyle m / \ beta}$ different colors. ^[6] For example, a planar graph with 16 vertices shown in the illustration has $m=24$ ${\ displaystyle m = 24}$ ribs. There is no perfect matching in this graph - if the central vertex belongs to the matching, the remaining vertices can be divided into three connected groups with the number of vertices 4, 5, 5. The resulting subgraphs with an odd number of vertices do not have a perfect matching. However, the graph has the maximum matching with seven edges, so $\beta =7$ ${\ displaystyle \ beta = 7}$ . Therefore, the number of colors required for the edge coloring of the graph is at least 24/7, and since the number of colors must be integer, we get at least 4 colors.

For regular degree graphs $k$ ${\ displaystyle k}$ without perfect matching, this lower bound can be used to show that at least $k+1$ ${\ displaystyle k + 1}$ colors. ^[6] In particular, this is true for regular graphs with an odd number of vertices. For such graphs, by the handshake lemma , $k$ ${\ displaystyle k}$ must in turn be odd. However inequality $\chi {\prime }\geqslant m\beta$ ${\ displaystyle \ chi {\ prime} \ geqslant m \ beta}$ does not fully explain the chromatic index of an arbitrary regular graph, because there are regular graphs that have perfect matching, but are not edge- k- coloringable. For example, the Petersen graph is regular with $m=15$ ${\ displaystyle m = 15}$ and with $\beta =5$ ${\ displaystyle \ beta = 5}$ ribs in perfect matching, but it does not have a 3-rib edge.

Relationship with Degree

Wiesing Theorem

Graph Chromatic Edge Number $G$ ${\ displaystyle G}$ closely related to the maximum degree ${\Delta }(G)$ ${\ displaystyle {\ Delta} (G)}$ (maximum number of edges adjacent to any single vertex of the graph $G$ ${\ displaystyle G}$ ) It's clear that $\chi {\prime }(G)\geq {\Delta }(G)$ ${\ displaystyle \ chi {\ prime} (G) \ geq {\ Delta} (G)}$ so if ${\Delta }$ ${\ displaystyle {\ Delta}}$ different edges contain a vertex $v$ ${\ displaystyle v}$ , then all these ribs should be painted in different colors, which is possible only if there is at least $\Delta$ ${\ displaystyle \ Delta}$ colors. Wiesing's theorem (named after Vadim Wiesing , who published it in 1964) states that this boundary is almost exact - for any graph, the edge chromatic number is either ${\Delta }(G)$ ${\ displaystyle {\ Delta} (G)}$ either $\Delta (G)+1$ ${\ displaystyle \ Delta (G) +1}$ . If a $\chi {\prime }(G)={\Delta }(G)$ ${\ displaystyle \ chi {\ prime} (G) = {\ Delta} (G)}$ , they say that G has class 1, otherwise they say about class 2.

Any bipartite graph has class 1 ^[7] and almost all random graphs have class 1 ^[8] . However, the task of checking whether an arbitrary graph has class 1 is an NP-complete problem ^[9] .

Wiesing ^[10] proved that planar graphs of maximal degree at least eight have class 1 and hypothesized that the same is true for planar graphs of degree 7 or 6. On the other hand, there are planar graphs with maximal degree from two to five, having class 2. Since then, the hypothesis has been proved for seven ^[11] . Planar graphs without bridges , Cubic graphs are of class 1, and this is equivalent to the formulation of the four-color problem ^[12] .

Regular graphs

The 1-factorization of k , a regular graph , that is, the decomposition of the edges of the graph into perfect matches , is the same as the edge k- coloring of the graph. Thus, a regular graph has 1-factorization if and only if it has class 1. A special case, a 3-color edge coloring of cubic (3-regular) graphs is sometimes called a Tait coloring .

Not every regular graph has 1-factorization. For example, Count Petersen does not. Snarks are defined as graphs that, like the Petersen graph, have no bridges, are 3-regular, and have class 2.

According to Koenig's theorem ^[7] , any bipartite regular graph has 1-factorization. The theorem was formulated earlier in terms of projective configurations and proved by Ernst Steinitz .

Multigraphs

Shannon's multigraph of the sixth degree, edge multiplicity three, requires nine colors for edge coloring

For multigraphs in which several edges can connect the same two vertices, similar to the Wizing theorem are known, but weaker results with respect to the edge chromatic number $\chi {\prime }(G)$ ${\ displaystyle \ chi {\ prime} (G)}$ maximum degree $\Delta (G)$ ${\ displaystyle \ Delta (G)}$ and multiplicity $\mu (G)$ ${\ displaystyle \ mu (G)}$ , the maximum number of edges in a bunch of parallel edges (that is, having the same end vertices). As a simple example showing that the Wiesing theorem is not generalized to multigraphs, consider the Shannon multigraph, a multigraph with three vertices and three connectives $\mu (G)$ ${\ displaystyle \ mu (G)}$ parallel edges connecting each pair of vertices. In this example: $\Delta (G)=2\mu (G)$ ${\ displaystyle \ Delta (G) = 2 \ mu (G)}$ - each vertex is adjacent to only two of the three bundles $\mu (G)$ ${\ displaystyle \ mu (G)}$ parallel edges, but the edge chromatic number is $3\mu (G)$ ${\ displaystyle 3 \ mu (G)}$ (in the column $3\mu (G)$ ${\ displaystyle 3 \ mu (G)}$ edges and any two edges are adjacent, so all edges must be painted in different colors). In a work inspired by Wiesing's theorem, Soifer and Shannon ^[13] ^[14] showed that this is the worst case - $\chi {\prime }(G)\leq (3/2)\Delta (G)$ ${\ displaystyle \ chi {\ prime} (G) \ leq (3/2) \ Delta (G)}$ for any multigraph $G$ ${\ displaystyle G}$ . In addition, for any multigraph $G$ ${\ displaystyle G}$ $\chi {\prime }(G)\leq \Delta (G)+\mu (G)$ ${\ displaystyle \ chi {\ prime} (G) \ leq \ Delta (G) + \ mu (G)}$ . This inequality reduces to the Wiesing theorem for simple graphs (for them $\mu (G)=1$ ${\ displaystyle \ mu (G) = 1}$ )

Algorithms

Since the task of checking whether a graph has class 1 is NP-complete , it is not known the time-polynomial edge coloring algorithm for any graph that gives the optimal coloring. However, a number of algorithms have been developed that weaken one or more criteria: they work on a subset of graphs, or they do not always give the optimal number of colors, or they do not always work in polynomial time.

Optimal coloring of some special graph classes

In the case of bipartite graphs or multigraphs with a maximum degree $\Delta$ ${\ displaystyle \ Delta}$ , the optimal number of colors is exactly the same $\Delta$ ${\ displaystyle \ Delta}$ . In 2001 ^[15] it was shown that the optimal edge coloring of these graphs can be found in almost linear time $O(m\,\log \Delta )$ ${\ displaystyle O (m \, \ log \ Delta)}$ where $m$ ${\ displaystyle m}$ Is the number of edges in the graph. Simpler, but somewhat slower algorithms were previously described by Cole and Hopcraft ^[16] and Alon ^[17] . Alon's algorithm begins by making the graph regular without significantly increasing the degree or significantly increasing the size by merging the pairs of vertices belonging to one share of the bipartite graph, and then adding a small number of vertices and edges. After that, if the degree is odd, Alon finds the perfect match for linear time, assigns him a color and removes it from the graph, which leads to an even degree graph. Finally, Alon uses Gabrov’s observation ^[18] that choosing alternating subsets of edges in an Eulerian cycle of a graph divides it into two regular subgraphs, transforming the edge coloring problem into two smaller problems, so that its algorithm now solves these two subtasks recursively . The total running time of the algorithm is estimated as $O(m\,\log m)$ ${\ displaystyle O (m \, \ log m)}$ .

For planar graphs with maximum degree ${\Delta }\geq 7$ ${\ displaystyle {\ Delta} \ geq 7}$ the optimal number of colors is exactly the same again $\Delta$ ${\ displaystyle \ Delta}$ . Under the stricter assumption that ${\Delta }\geq 9$ ${\ displaystyle {\ Delta} \ geq 9}$ , one can find the optimal edge coloring in linear time ^[19] .

Algorithms that use more colors than necessary for optimal coloring

There are algorithms for polynomial time coloring of any graph with $\Delta +1$ ${\ displaystyle \ Delta +1}$ colors, which corresponds to the boundary defined by Vizing's theorem ^[20] ^[21] .

For multigraphs in 1987 ^[22] , the following algorithm exists (attributed to ): the original multigraph $G$ ${\ displaystyle G}$ becomes Euler by adding a vertex connected by edges to all vertices of an odd degree; the Euler path is found, the orientation for this path is selected; a bipartite graph is created $H$ ${\ displaystyle H}$ which contains two copies of each vertex of the graph $G$ ${\ displaystyle G}$ , one in each lobe, and ribs from the top $u$ ${\ displaystyle u}$ in the left lobe to the top $v$ ${\ displaystyle v}$ in the right lobe when the oriented path has an arc of $u$ ${\ displaystyle u}$ at $v$ ${\ displaystyle v}$ in the graph $G$ ${\ displaystyle G}$ . Next, the edge coloring algorithm of the bipartite graph for the graph is applied. $H$ ${\ displaystyle H}$ . Every color in $H$ ${\ displaystyle H}$ corresponds to the set of edges in $G$ ${\ displaystyle G}$ , which forms a subgraph with a maximum degree of two, that is, a disconnected union of paths and loops so that for each color in $H$ ${\ displaystyle H}$ three colors can be formed in $G$ ${\ displaystyle G}$ . The running time of the algorithm is limited by the time of coloring the bipartite graph. $O(m\,\log \Delta )$ ${\ displaystyle O (m \, \ log \ Delta)}$ when using the algorithm of Cole, Ost and Shirr ^[15] . The number of colors that this algorithm uses does not exceed $3\left\lceil {\frac {\Delta }{2}}\right\rceil$ ${\ displaystyle 3 \ left \ lceil {\ frac {\ Delta} {2}} \ right \ rceil}$ which is close but not quite the same as the Shannon border $\left\lfloor {\frac {3\Delta }{2}}\right\rfloor$ ${\ displaystyle \ left \ lfloor {\ frac {3 \ Delta} {2}} \ right \ rfloor}$ . The same can be done using a parallel algorithm directly. In the same article, Karloff and Schmoys also propose an algorithm with linear runtime for coloring multigraphs with a maximum of the third degree in four colors (which satisfies both the Shannon boundary and the Vizing boundary). This algorithm works on similar principles - the algorithm also adds a vertex to make the graph Euler, finds the Euler path, and then selects alternating sets of edges in the path to split the graph into two subsets of maximal degree two. The paths and even cycles of each subset can be painted in two colors (two colors per subgraph). The next step is coloring the edges of the odd cycles in which at least one edge can be painted with one of two colors belonging to the opposite subgraph. Removing this edge from an odd cycle leaves a path that can be colored with two colors.

The greedy coloring algorithm, which selects the edges of a graph or multigraph sequentially and assigns the first valid color, can sometimes use $2{\Delta }-1$ ${\ displaystyle 2 {\ Delta} -1}$ colors, which can almost double the required number of colors. However, it has the advantage that it can be used in that do not know anything in advance about the structure of the graph. Under these conditions, its is two, and this coefficient is optimal - no other algorithm can give better indicators ^[23] . However, if the edges arrive in random order and the original graph has a degree of at least logarithmic, you can get a lower competitive coefficient ^[24] .

Some authors have hypothesized that the fractional chromatic index of any multigraph (a number that can be calculated in polynomial time using linear programming ) differs from the chromatic index by no more than one ^[25] . If the hypothesis is true, it will be possible to find a number that does not differ from the chromatic index by more than one in the case of multigraphs, which corresponds to the Wizing theorem for simple graphs. Although, in the general case, the hypothesis has not been proved, it is known that it is true if the chromatic index is not less than ${\Delta }+{\sqrt {{\Delta }/2}}$ ${\ displaystyle {\ Delta} + {\ sqrt {{\ Delta} / 2}}}$ , exactly the same as in the case of multigraphs with a sufficiently large multiplicity ^[26] .

Exact Algorithms

It is simple to check whether it is possible to colorfully graph a graph with one or two colors so that the first nontrivial case of coloring is to check whether it is possible to color a graph graphically with three colors. In 2009 ^[27] it was shown that it is possible to check whether an edge coloring of a graph by three colors exists in time $O(1.344^{n})$ ${\ displaystyle O (1.344 ^ {n})}$ when using only polynomial space. Although these time boundaries are exponential, it is significantly faster than brute force search by looking at all possible colorings of the edges. Any doubly connected 3-regular graph with $n$ ${\ displaystyle n}$ peaks has $O(2^{n/2})$ ${\ displaystyle O (2 ^ {n / 2})}$ 3-sided colorings. And all of them can be listed in time $O(2^{n/2})$ ${\ displaystyle O (2 ^ {n / 2})}$ (a little slower than the search time for one coloring). As noted, the prism count over $n/2$ {\ displaystyle n / 2} -gon, has many colorings, which shows that this boundary is exact ^[28] .

When applying exact coloring algorithms for the vertices of an edge graph , we can edge-optimally color any graph with $m$ ${\ displaystyle m}$ edges, regardless of the number of colors needed per time $2^{m}m^{O(1)}$ ${\ displaystyle 2 ^ {m} m ^ {O (1)}}$ using exponential space, or in time $O(2.2461^{m})$ ${\ displaystyle O (2.2461 ^ {m})}$ and polynomial space ^[29] .

Since the task of edge coloring is NP-complete even for three colors, it is unlikely to give in to a by the number of colors. However, the task can be parameterized by other parameters. In particular, Zhou, Nakano, and Nishiseki ^[30] showed that for graphs with wood width $w$ ${\ displaystyle w}$ optimal edge coloring can be found in time $O(nw(6w)^{w(w+1)/2})$ ${\ displaystyle O (nw (6w) ^ {w (w + 1) / 2})}$ which grows exponentially from $w$ ${\ displaystyle w}$ , but only linearly from the number of vertices of the graph $n$ ${\ displaystyle n}$ .

In 1991 ^[31] , the edge coloring problem was formulated as an integer programming problem and experiments were carried out using integer programming packages for edge coloring of graphs; however, no analysis of the complexity of such algorithms is given.

Additional properties

Uniquely 3-colorable generalized Petersen graph

G(9,2)

{\ displaystyle G (9.2)}

. One of the three colors is shown by light edges, the other two colors can be obtained by turning these edges by 40 ° in both directions or by alternately coloring the Hamiltonian cycle in two colors.

The graph is uniquely edge $k$ ${\ displaystyle k}$ -colored if and only if there is only one way to break the edges into $k$ ${\ displaystyle k}$ color classes, not counting $k!$ ${\ displaystyle k!}$ possible permutations of colors. For $k\neq 3$ ${\ displaystyle k \ neq 3}$ definitely rib $k$ ${\ displaystyle k}$ -colorable graphs are only paths, cycles, and stars , but for $k=3$ ${\ displaystyle k = 3}$ can be definitely edge $k$ ${\ displaystyle k}$ -colorable and other graphs. Any uniquely edge 3-colorable graph has exactly three Hamiltonian cycles (formed by removing one of the three colors), however, there are 3-regular graphs having three Hamiltonian cycles but not having a unique 3-coloring edge, such as, for example, generalized Petersen graphs $G(6n+3,2)$ ${\ displaystyle G (6n + 3,2)}$ for $n\geq 2$ ${\ displaystyle n \ geq 2}$ . Only one nonplanar uniquely edge 3-colorable graph is known; this is a generalized Petersen graph $G(9,2)$ ${\ displaystyle G (9.2)}$ , and there is a hypothesis that others do not exist ^[32] .

A complete bipartite graph K _3.3 with all three of its colors drawn as parallel lines.

Folkman and Fulkerson ^[33] investigated non-increasing sequences of numbers $m_{1},m_{2},m_{3},...$ ${\ displaystyle m_ {1}, m_ {2}, m_ {3}, ...}$ for which there exists an edge coloring of a given graph $G$ ${\ displaystyle G}$ with $m_{1}$ ${\ displaystyle m_ {1}}$ ribs of the first color $m_{2}$ ${\ displaystyle m_ {2}}$ ribs of the second color, and so on. They noticed that if the sequence $P$ ${\ displaystyle P}$ fits in the described sense, and if it is lexicographically larger than the sequence $Q$ ${\ displaystyle Q}$ with the same amount then $Q$ ${\ displaystyle Q}$ also suitable. If $P>Q$ ${\ displaystyle P> Q}$ lexicographically $P$ ${\ displaystyle P}$ can be converted to $Q$ ${\ displaystyle Q}$ step by step, decreasing at one step one of the numbers $m_{i}$ ${\ displaystyle m_ {i}}$ by one and increasing another, the next number $m_{j}$ ${\ displaystyle m_ {j}}$ ( $i<j$ ${\ displaystyle i <j}$ ), per unit. In terms of edge coloring, we start with coloring $P$ ${\ displaystyle P}$ , then successively exchange the color $i$ ${\ displaystyle i}$ and $j$ ${\ displaystyle j}$ in , the largest path of ribs alternating two colors. In particular, any graph has a fair edge coloring, an edge coloring with the optimal number of colors, in which two color classes differ in size by a maximum of one.

can be used to transfer many edge coloring properties from finite graphs to infinite ones . For example, Shannon and Wiesing's theorems on the relation between the degree of a graph and its chromatic index are both easily generalized to infinite graphs ^[34] .

In 2011 ^[35], the problem of finding a picture of a given cubic graph with the properties that all the edges in the figure have one of three different tilt angles and no two edges lie on one straight line was considered. If such a representation of the graph in the figure exists, it is clear that the angle of inclination of the edges can be considered as the color of the edges in the three-color coloring of the graph. For example, a drawing $K_{3,3}$ ${\ displaystyle K_ {3,3}}$ in the form of edges and long diagonals of a regular hexagon, represents a 3-edge edge coloring of the graph in this way. It is shown that a 3-regular bipartite graph with a given Tait coloring has a graphical representation of this form if and only if it is edge-k-connected . For non-bipartite graphs, the condition is slightly more complicated - a given coloring can be represented by such a pattern if the graph is 3-edge connected and if the removal of two equally colored edges leads to a non-bipartite subgraph. All these conditions are easy to verify in polynomial time, but the task of checking whether a 4-colored 4-regular graph edge graph with four slope angles corresponding to the colors is complete for the , of the same complexity class, as NP-completeness.

Having a connection with the maximum degree and maximum number of graph matches, the chromatic index is also closely related to the arboreal $la(G)$ ${\ displaystyle la (G)}$ count $G$ ${\ displaystyle G}$ , the minimum number of linear forests (incoherent union of paths) into which the edges of the graph can be split. Matching is a special kind of linear forest, but, on the other hand, any linear forest can be edge-colored 2-color, so for any $G$ ${\ displaystyle G}$ $la(G)\leq \chi {\prime }(G)\leq 2la(G)$ ${\ displaystyle la (G) \ leq \ chi {\ prime} (G) \ leq 2la (G)}$ . Akiyama's hypothesis states that $\mathop {\mathrm {la} } (G)\leq \left\lceil {\frac {{\Delta }+1}{2}}\right\rceil$ ${\ displaystyle \ mathop {\ mathrm {la}} (G) \ leq \ left \ lceil {\ frac {{\ Delta} +1} {2}} \ right \ rceil}$ , which would result in a stronger inequality $2la(G)-2\leq \chi {\prime }(G)\leq 2la(G)$ ${\ displaystyle 2la (G) -2 \ leq \ chi {\ prime} (G) \ leq 2la (G)}$ . For graphs of maximum degree three $la(G)$ ${\ displaystyle la (G)}$ always exactly equal to two, so the restriction $\chi {\prime }(G)\leq 2la(G)$ ${\ displaystyle \ chi {\ prime} (G) \ leq 2la (G)}$ corresponds to the boundary following from Wiesing's theorem ^[36] .

Other types of edge coloring

A partition of the complete bipartite graph K _4.4 into three forests, showing that the graph has three trees.

The Thue number of a graph is the number of colors needed for an edge coloring that satisfies more stringent requirements than any path of even length, namely the first and second half of the path must form different color sequences.

A graph's wood is the minimum number of colors needed for coloring in such a way that edges of any color do not contain cycles (and not as in the standard coloring task - edges of the same color are not adjacent). Thus, this is the minimum number of forest elements into which the edges of the graph can be expanded ^[37] . Unlike the chromatic number, the width of the forest can be calculated in polynomial time ^[38] .

is a task in which for a given graph, for each arc of which a list of colors is given, you need to find a suitable coloring of edges in which each color is taken from a given list. Prescribed Chromatic Index Graph $G$ ${\ displaystyle G}$ Is the smallest number $k$ ${\ displaystyle k}$ in which, regardless of the choice of color lists for edges, if at least at least one edge is specified $k$ ${\ displaystyle k}$ colors, coloring is guaranteed to exist. The prescribed chromatic index is always no less than the chromatic number. about filling in partial Latin squares can be rephrased as the statement that the prescribed edge chromatic number of a complete bipartite graph $K_{n,n}$ ${\ displaystyle K_ {n, n}}$ equal to its edge chromatic number $n$ ${\ displaystyle n}$ . In 1995 ^{[39] the} hypothesis was resolved, moreover, a stronger statement was proved that for any bipartite graph, the chromatic index and the prescribed chromatic index are equal. An even more general hypothesis was made about the equality of the chromatic number and the prescribed chromatic number for arbitrary multigraphs without loops. This hypothesis remains open.

Many variations of the vertex coloring problem studied have been extended to edge coloring. For example, the problem of full edge coloring is a variant of full coloring , correct coloring of vertices, in which any pair of colors should be present at least once in the set of conjugate vertices, and the task is to maximize the total number of colors ^[40] . Strict edge coloring is an edge version of , in which any two edges with adjacent end vertices must have different colors ^[41] . Strict edge coloring is used in for wireless networks ^[42] . Acyclic edge coloring is a variant of acyclic coloring in which any two colors form an acyclic subgraph (that is, a forest) ^[43] .

In 2008 ^[28] , the edge 3-coloring of cubic graphs was studied with the additional property that no two two-color cycles have more than one common edge, in particular, it was shown that the existence of such a coloring is equivalent to the existence of a graph on a three-dimensional integer lattice with edges on lines parallel to the coordinate axes, and each such line contains a maximum of two vertices. However, as in the case of the standard edge 3-coloring problem, finding a coloring of this type is an NP-complete problem.

Total coloring is a type of coloring combining vertex and edge coloring, in which both vertices and edges are painted. Any vertex and edge whose end it is, or two adjacent edges must have different colors, as well as two adjacent vertices. There is a hypothesis (combining Wiesing's theorem and Brooks' theorem ) that any graph has a total coloring in which the number of colors does not exceed the maximum degree plus two. The hypothesis is not proven.

If a 3-regular graph on a surface is edge-3-colored, its dual graph forms a triangulation of the surface, which is also edge-colored (although, in the general case, the edge coloring is wrong) in the sense that each triangle is colored in three colors - edge on color . Other coloring and orientation of the triangles, along with other local restrictions on how colors are distributed over the vertices or faces of the triangulation, can be used to encode some types of geometric objects. For example, rectangular splittings (parts of a rectangular division of a rectangle into smaller rectangles, with three rectangles at each point) can be described combinatorially by “regular marking”, two-color coloring of the edges of a triangulation graph dual to rectangular fragmentation, with the restriction that the edges adjacent to each vertex , form four groups of edges running (clockwise) in a row. Inside each group, the ribs are painted in the same color and have the same direction. This marking is dual to the coloring of the crushing itself, in which the vertical edges have one color and the horizontal edges have a different color. Similar local restrictions on the order of colored edges for a vertex can be used to code the embedding of planar graphs in a grid formed by straight lines and three-dimensional polyhedra with faces parallel to coordinate planes. For each of these three types of regular marking, the set of regular markings forms a distributive lattice , which can be used to quickly list all geometric structures based on the same graph, or to find a structure that satisfies additional restrictions ^[44] .

can be represented as a directed graph in which each vertex has the same semi-degree of the outcome of the vertices and in which the edges $d$ ${\ displaystyle d}$ -painted so that any two edges with the same initial vertex have different colors. The task of coloring roads is the task of edge coloring of a directed graph with the same semi-degree of outcome, such that the resulting automaton has a synchronized word . Trakhtman ( Trakhtman 2009 ) solved the problem of coloring roads, proving that such a coloring can be found if a given graph is strongly connected and .

Ramsey's theorem concerns the problem $k$ ${\ displaystyle k}$ coloring of edges of a large complete graph $K_{n}$ ${\ displaystyle K_ {n}}$ in order to avoid creating full-color monochrome subgraphs $K_{s}$ ${\ displaystyle K_ {s}}$ some given size $s$ ${\ displaystyle s}$ . According to the theorem, there exists a number $R_{k}(s)$ ${\ displaystyle R_ {k} (s)}$ such that with $n\geq R(s)$ ${\ displaystyle n \ geq R (s)}$ the specified coloring is not possible. For example, $R_{2}(3)=6$ ${\ displaystyle R_ {2} (3) = 6}$ , which means that if the edges of the graph $K_{6}$ ${\ displaystyle K_ {6}}$ 2-colored, there is always a monochrome triangle.

Applications

The edge coloring of full graphs can be used to split the schedule in round robin tournaments into several circles, so that each pair plays in one of the circles. In this application, the vertices correspond to the participants of the tournament, and the edges correspond to the games. The color of the edges corresponds to the circles of the tournament ^[45] . A similar coloring technique can be used to create other sports schedules, in which not everyone plays with everyone. For example, in the national football league (USA, American football ), the pairs of teams that will play this year are determined by the results of the teams in the previous year, and the edge coloring algorithm is applied to the graph formed by the set of these pairs in order to distribute games for the weekend, according to by which games occur ^[46] . For this application, Vizing's theorem means that it does not matter how many pairs are selected (if no two teams play twice a season), it is always possible to find a schedule that captures a maximum of one extra weekend (compared to the number of games of one team).

is the task of planning a production process in which there are many objects that require manufacturing. Each object must go through some procedures (in any order) and each work must be carried out on a specific machine, while the machine can only perform one procedure at a time. If all the works have the same length, then the problem can be posed as the edge coloring of a bipartite graph, in which the vertices of one share represent the objects to be manufactured, and the processing machines represent the vertices of the other share of the graph. Ribs represent the work that needs to be done, and colors represent the time intervals in which the work needs to be done. Since the edge coloring of a bipartite graph can be done in polynomial time, the same is true for the indicated special case of the schedule for an open line ^[47] .

In 2005 ^[48] , the connection schedule problem for a time-division multiple access communication protocol in wireless sensor networks was studied as an option for edge coloring. In this problem, you need to select the time intervals for the edges of the wireless network so that each vertex of the network can communicate with neighboring vertices without mutual influence. The use of strict edge coloring (with two time intervals for each color of the edges, one in each direction) solves the problem, but the number of spaces used may be more than necessary. Instead, they looked for a coloring of the oriented graph formed by replacing each non-oriented edge with two oriented arcs, with each arc $u v$ ${\ displaystyle uv}$ must have a color different from the colors of the arcs emanating from $v$ ${\ displaystyle v}$ and neighbors $v$ ${\ displaystyle v}$ . They proposed a heuristic algorithm for solving this problem, based on a distributed algorithm for edge $({\Delta }+1)$ ${\ displaystyle ({\ Delta} +1)}$ -coloring with the subsequent process of correcting the schedule to remove possible mutual interference.

In fiber-optic communication, the task of is the task of assigning the frequency of light to a pair of vertices for which communication is required, and paths through an optical fiber network for each pair, while there is a limitation that no two paths use one for a common fiber segment same frequency. Paths passing through the same switch, but not through the same fiber segment, are allowed to have the same frequency. If the network is built in the form of a star with a single commutator in the center, which is connected by a separate fiber to each vertex of the network, the color assignment problem can be modeled exactly like the task of coloring the edges of a graph or a multigraph, in which communication nodes form the vertices of the graph, pairs of nodes that need exchange of information, form arcs, and the frequency that can be used for each pair of nodes corresponds to the coloring of arcs in the coloring task. For communication networks having a more general tree topology, local solutions to the path color assignment problems for stars formed by each communicator can be brought together to obtain a single global solution ^[49] .

Open Issues

Jensen and Toft ^[50] listed 23 open problems regarding edge coloring. These include:

The Goldberg hypothesis ^[51] that the chromatic index and fractional index differ by no more than one, which would allow us to approximate the chromatic index with an error of one color in polynomial time.
Some hypotheses of Jakobsen and other authors on the structure of critical graphs for edge coloring of class 2 graphs such that any subgraph either has a lower maximum degree or has class 1. Jacobsen initially suggested that all critical graphs have an odd number of vertices, but, ultimately, the assumption is refuted. Several other hypotheses weaker than this, as well as hypotheses limiting the number of vertices of critical graphs and critical multigraphs, remain open.
Wiesing's task of classifying maximum degrees, which is possible for planar graphs of class 2.
Hilton overflow graph hypothesis (AJW Hilton), which states that a graph with degree no less $n/3$ ${\ displaystyle n / 3}$ either has class 1 or contains a subgraph of the same degree $\Delta$ ${\ displaystyle \ Delta}$ as the original graph, but for an odd number of vertices $k$ ${\ displaystyle k}$ such that the number of edges of the subgraph is greater $\Delta (k-1)/2$ ${\ displaystyle \ Delta (k-1) / 2}$ . The hypothesis of and Paul Seymour regarding planar graphs instead of graphs of a high degree is close to this.
The hypothesis of Chetwynd and Hilton (possibly having roots in earlier works) that a regular graph with an even number of vertices $n$ ${\ displaystyle n}$ and at least $n/2$ ${\ displaystyle n / 2}$ has class 1.
The hypothesis of and that 6-regular multigraphs formed by doubling each edge of a 3-regular simple graph without bridges can be colored with six colors.
The hypothesis of Fiorini and Wilson that any planar graphs without triangles , other than the K _1.3 claw , are not color -coded uniquely in 3 colors.

The more modern hypothesis is also noteworthy: if $G$ ${\ displaystyle G}$ is an $d$ ${\ displaystyle d}$ -regular planar multigraph then $G$ ${\ displaystyle G}$ rib $d$ ${\ displaystyle d}$ -colored if and only if $G$ ${\ displaystyle G}$ odd edge $d$ ${\ displaystyle d}$ -connected. This hypothesis can be considered as a generalization of the problem of four colors for $d=3$ ${\ displaystyle d = 3}$ . , Katherine Edwards, and Paul Seymour proved that the 8-regular planar multigraph has an edge chromatic number of 8 ^[52] .

Notes

↑ Soifer, 2008 , problem 16.4, p. 133.
↑ Soifer, 2008 .
↑ Soifer, 2008 , Problem 16.5, p. 133. The fact that you need either $n$ ${\ displaystyle n}$ either $(n-1)$ ${\ displaystyle (n-1)}$ colors follows from Wiesing's theorem .
↑ Biggs, 1972 .
↑ Biggs, 1972 ; Meredith, Lloyd, 1973 ; Bigs, 1979 .
↑ ¹ ² Soifer, 2008 , p. 134.
↑ ¹ ² König, 1916 .
↑ Erdös, Wilson, 1977 .
↑ Holler, 1981 .
↑ Wiesing, 1965 .
↑ Sanders, Zhao, 2001 .
↑ Tight, 1880 ; Appel, Haken, 1976 .
↑ Soifer, 2008 , p. 136.
↑ Shannon, 1949 .
↑ ¹ ² Cole, Ost, Shirra, 2001 .
↑ Cole, Hopcroft, 1982 .
↑ Alon, 2003 .
↑ Gabrov, 1976 .
↑ Cole, Kovalik, 2008 .
↑ Misra, Grize, 1992 .
↑ Gabrov et al., 1985 .
↑ Carlof, Schmoys, 1987 .
↑ Bar Noi, Motwani, Naor, 1992 .
↑ Bahmani, Mehta, Motwani, 2010 .
↑ Goldberg, 1973 , Andersen, 1977 ; Seymour, 1979 .
↑ Chen, Yu, Zang, 2011 .
↑ Kovalik, 2009 .
↑ ¹ ² Epstein, 2008 .
↑ Björklund, Husfeld, Koivisto, 2009 .
↑ Zhou, Nakano, Nishiseki, 1996 .
↑ Nemhauser, Park, 1991 .
↑ Schwenk, 1989 .
↑ Folkman, Fulkerson, 1969 .
↑ Bosak, 1972 .
↑ Richter, 2011 .
↑ Akiyama, Ikzu, Harari, 1980 , Habib, Peroshe, 1982 , Horak, Nipel, 1982 .
↑ Nash-Williams, 1964 .
↑ Gabrov, Westerman, 1992 .
↑ Galvin, 1995 .
↑ Bosak, Neschetril, 1976 .
↑ Fouquet, Jolive, 1983 ; Mahdian, 2002 ; Frieze, Krivelevich, Sudakov, 2005 ; Cranston, 2006 .
↑ Barrett et al., 2006 .
↑ Alon, Sudakov, Sax, 2001 , Muthu, Narayanan, Subramanyan, 2007 .
↑ Epstein, 2010 .
↑ Burke, Verra, Kingston, 2004 .
↑ Skien, 2008 .
↑ Williamson et al., 1997 .
↑ Gandham, Dawanda, Prakash, 2005 .
↑ Elebach, Jensen, 2001 .
↑ Jensen, Toft, 1995 .
↑ Goldberg, 1973 .
↑ Maria Chudnovsky, Katherine Edwards, Paul Seymour. Edge-coloring eight-regular planar graphs (neopr.) . - 2012 .-- 13 January.

Links

Jin Akiyama, Geoffrey Exoo, Frank Harary. Covering and packing in graphs. III. Cyclic and acyclic invariants // Mathematica Slovaca. - 1980. - T. 30 , no. 4 . - S. 405-417 .
Noga Alon. A simple algorithm for edge-coloring bipartite multigraphs // Information Processing Letters. - 2003. - T. 85 , no. 6 . - S. 301-302 . - DOI : 10.1016 / S0020-0190 (02) 00446-5 .
Noga Alon, Benny Sudakov, Ayal Zaks. Acyclic edge colorings of graphs // Journal of Graph Theory. - 2001. - T. 37 , no. 3 . - S. 157-167 . - DOI : 10.1002 / jgt . 1010 .
Lars Dovling Andersen. On edge-colors of graphs // Mathematica Scandinavica. - 1977. - T. 40 , no. 2 . - S. 161-175 . . As quoted in ^[1]
K. Appel, W. Haken. Every planar map is four colorable // English Bulletin of the American Mathematical Society. - 1976. - Vol. 82 , iss. 5 . - P. 711-712 . - DOI : 10.1090 / S0002-9904-1976-14122-5 .
Bahman Bahmani, Aranyak Mehta, Rajeev Motwani. Proceedings of the Twenty-First Annual ACM-SIAM Symposium on Discrete Algorithms (SODA '10). - 2010 .-- S. 31-39 .
Amotz Bar-Noy, Rajeev Motwani, Joseph Naor. The greedy algorithm is optimal for on-line edge coloring // Information Processing Letters. - 1992. - T. 44 , no. 5 . - S. 251-253 . - DOI : 10.1016 / 0020-0190 (92) 90209-E .
CL Barrett, G. Istrate, VSA Kumar, MV Marathe, S. Thite, S. Thulasidasan. Proc. Fourth Annual IEEE International Conference on Pervasive Computing and Communications Workshops (PerCom Workshops 2006). - 2006 .-- S. 106 . - ISBN 0-7695-2520-2 . - DOI : 10.1109 / PERCOMW.2006.129 .
Norman Biggs. Research Problems / Richard K. Guy. - American Mathematical Monthly. - 1972. - T. 79 .-- S. 1018-1020.
Norman Biggs. Second International Conference on Combinatorial Mathematics // Annals of the New York Academy of Sciences. - 1979.- T. 319 . - S. 71-81 . - DOI : 10.1111 / j.1749-6632.1979.tb32775.x .
Andreas Bjorklund, Thore Husfeldt, Mikko Koivisto. Set partitioning via inclusion-exclusion // SIAM Journal on Computing. - 2009. - T. 39 , no. 2 . - S. 546-563 . - DOI : 10.1137 / 070683933 .
Juraj Bosak. Chromatic index of finite and infinite graphs // Czechoslovak Mathematical Journal. - 1972.- T. 22 (97) . - S. 272-290 .
Juraj Bosak, Jaroslav Nesetril. Complete and pseudocomplete colors of a graph // Matematicky Casopis Slovenskej Akademie Vied. - 1976. - T. 26 , no. 3 . - S. 171-184 .
E. Burke, D. De Werra, J. Kingston. {{{title}}} / JL Gross, J. Yellen. - CRC Press, 2004 .-- S. 462 . - ISBN 978-1-58488-090-5 .
Guantao Chen, Xingxing Yu, Wenan Zang. Approximating the chromatic index of multigraphs // Journal of Combinatorial Optimization. - 2011 .-- T. 21 , no. 2 . - S. 219-246 . - DOI : 10.1007 / s10878-009-9232-y .
Richard Cole, John Hopcroft. On edge coloring bipartite graphs // SIAM Journal on Computing. - 1982. - T. 11 , no. 3 . - S. 540-546 . - DOI : 10.1137 / 0211043 .
Richard Cole, Lukasz Kowalik. New linear-time algorithms for edge-coloring planar graphs // Algorithmica. - 2008. - T. 50 , no. 3 . - S. 351-368 . - DOI : 10.1007 / s00453-007-9044-3 .
Richard Cole, Kirstin Ost, Stefan Schirra. Edge-coloring bipartite multigraphs in $O(E\log D)$ ${\ displaystyle O (E \ log D)}$ time // Combinatorica . - 2001. - T. 21 , no. 1 . - S. 5-12 . - DOI : 10.1007 / s004930170002 .
Daniel W. Cranston. Strong edge-coloring of graphs with maximum degree 4 using 22 colors // Discrete Mathematics . - 2006. - T. 306 , no. 21 . - S. 2772-2778 . - DOI : 10.1016 / j.disc.2006.03.05.03 .
David Eppstein Proc. 16th Int. Symp Graph Drawing / Ioannis G. Tollis, Marizio Patrignani. - Heraklion, Crete, 2008 .-- T. 5417. - S. 78-89. - (Lecture Notes in Computer Science).
David Eppstein Proc. 22nd Canadian Conference on Computational Geometry (CCCG 2010). - 2010.
Paul Erdos, Robin J. Wilson. Note on the chromatic index of almost all graphs // Journal of Combinatorial Theory . - 1977. - T. 23 , no. 2-3 . - S. 255—257 . - DOI : 10.1016 / 0095-8956 (77) 90039-9 .
Thomas Erlebach, Klaus Jansen. The complexity of path coloring and call scheduling // Theoretical Computer Science. - 2001. - T. 255 , no. 1-2 . - S. 33-50 . - DOI : 10.1016 / S0304-3975 (99) 00152-8 .
S. Fiorini, RJ Wilson. Edge-colors of graphs. - London: Pitman, 1977. - T. 16. - (Research Notes in Mathematics). - ISBN 0-273-01129-4 .
Jon Folkman, DR Fulkerson. Combinatorial Mathematics and its Applications (Proc. Conf., Univ. North Carolina, Chapel Hill, NC, 1967). - Chapel Hill, NC: Univ. North Carolina Press, 1969. - S. 561-577.
J.-L. Fouquet, J.-L. Jolivet. Strong edge-colorings of graphs and applications to multi $k$ ${\ displaystyle k}$ -gons // Ars Combinatoria. - 1983 .-- T. 16 , no. A. - S. 141-150 .
Alan M. Frieze, Michael Krivelevich, Benny Sudakov. The strong chromatic index of random graphs // SIAM Journal on Discrete Mathematics . - 2005. - T. 19 , no. 3 . - S. 719-727 (electronic) . - DOI : 10.1137 / S0895480104445757 .
Harold N. Gabow. Using Euler partitions to edge color bipartite multigraphs // International Journal of Computer and Information Sciences. - 1976. - T. 5 , no. 4 . - S. 345-355 . - DOI : 10.1007 / BF00998632 .
Harold N. Gabow, Takao Nishizeki, Oded Kariv, Daniel Leven, Osamu Terada. Algorithms for edge-coloring graphs. - Tohoku University, 1985.
Harold N. Gabow, Herbert H. Westermann. Forests, frames, and games: algorithms for matroid sums and applications // Algorithmica. - 1992. - T. 7 , no. 5-6 . - S. 465-497 . - DOI : 10.1007 / BF01758774 .
F. Galvin. The list chromatic index of a bipartite multigraph // Journal of Combinatorial Theory . - 1995. - T. 63 , no. 1 . - S. 153-158 . - DOI : 10.1006 / jctb.1995.1011 .
S. Gandham, M. Dawande, R. Prakash. Proc. 24th INFOCOM. - 2005 .-- T. 4 . - S. 2492-2501 . - ISBN 0-7803-8968-9 . - DOI : 10.1109 / INFCOM.2005.1498534 .
MK Gol'dberg. Multigraphs with a chromatic index that is nearly maximal // Diskret. Analiz .. - 1973. - Vol. 23 . - S. 3-7, 72 . . As cited in ^[1] .
M. Habib, B. Peroche. Some problems about linear arboricity // Discrete Mathematics. - 1982. - T. 41 , no. 2 . - S. 219-220 . - DOI : 10.1016 / 0012-365X (82) 90209-6 .
Ian Holyer. The NP-completeness of edge-coloring // SIAM Journal on Computing . - 1981. - T. 10 , no. 4 . - S. 718-720 . - DOI : 10.1137 / 0210055 .
Peter Horak, Ludovit Niepel. A short proof of a linear arboricity theorem for cubic graphs // Acta Mathematica Universitatis Comenianae. - 1982.- T. 40/41 . - S. 275-277 .
Tommy R. Jensen, Bjarne Toft. Graph Coloring Problems. - New York: Wiley-Interscience, 1995 .-- ISBN 0-471-02865-7 .
Howard J. Karloff, David Shmoys. Efficient parallel algorithms for edge coloring problems // Journal of Algorithms. - 1987. - T. 8 , no. 1 . - S. 39-52 . - DOI : 10.1016 / 0196-6774 (87) 90026-5 .
Uber Graphen und ihre Anwendung auf Determinantentheorie und Mengenlehre // Mathematische Annalen . - 1916. - T. 77 , no. 4 . - S. 453-465 . - DOI : 10.1007 / BF01456961 .
Lukasz Kowalik. Improved edge-coloring with three colors // Theoretical Computer Science. - 2009.- T. 410 , no. 38-40 . - S. 3733-3742 . - DOI : 10.1016 / j.tcs.2009.05.05.005 .
Mohammad Mahdian. On the computational complexity of strong edge coloring // Discrete Applied Mathematics. - 2002. - T. 118 , no. 3 . - S. 239-248 . - DOI : 10.1016 / S0166-218X (01) 00237-2 .
Guy HJ Meredith, E. Keith Lloyd. The footballers of Croam // Journal of Combinatorial Theory . - 1973. - T. 15 , no. 2 . - S. 161-166 . - DOI : 10.1016 / 0095-8956 (73) 90016-6 .
J. Misra, D. Gries. A constructive proof of Vizing's Theorem // Information Processing Letters . - 1992. - T. 41 , no. 3 . - S. 131-133 . - DOI : 10.1016 / 0020-0190 (92) 90041-S .
Rahul Muthu, N. Narayanan, CR Subramanian. Improved bounds on acyclic edge coloring // Discrete Mathematics . - 2007.- T. 307 , no. 23 . - S. 3063-3069 . - DOI : 10.1016 / j.disc.2007.03.03.006 .
Crispin Nash-Williams. Decomposition of finite graphs into forests // Journal of the London Mathematical Society. - 1964 .-- T. 39 .
George Nemhauser, Sungsoo Park. A polyhedral approach to edge coloring // Operations Research Letters. - 1991. - T. 10 , no. 6 . - S. 315-322 . - DOI : 10.1016 / 0167-6377 (91) 90003-8 .
David A. Richter. Proc. 18th International Symposium on Graph Drawing (GD 2010) / Ulrik Brandes, Sabine Cornelsen. - Springer-Verlag, 2011 .-- T. 6502 .-- S. 353-364. - (Lecture Notes in Computer Science). - ISBN 978-3-642-18468-0 . - DOI : 10.1007 / 978-3-642-18469-7_32 .
Daniel P. Sanders, Yue Zhao. Planar graphs of maximum degree seven are class I // Journal of Combinatorial Theory . - 2001. - T. 83 , no. 2 . - S. 201-212 . - DOI : 10.1006 / jctb.2001.2047 .
PD Seymour. On multicolourings of cubic graphs, and conjectures of Fulkerson and Tutte // Proceedings of the London Mathematical Society. - 1979. - T. 38 , no. 3 . - S. 423-460 . - DOI : 10.1112 / plms / s3-38.3.423 .
Allen J. Schwenk. Enumeration of Hamiltonian cycles in certain generalized Petersen graphs // Journal of Combinatorial Theory . - 1989.- T. 47 , no. 1 . - S. 53-59 . - DOI : 10.1016 / 0095-8956 (89) 90064-6 .
Claude Shannon. A theorem on coloring the lines of a network // J. Math. Physics. - 1949.- T. 28 . - S. 148-151 .
Steven S. Skiena. The Algorithm Design Manual. - Springer-Verlag, 2008 .-- S. 548-550 . - ISBN 978-1-84800-069-8 . - DOI : 10.1007 / 978-1-84800-070-4_16 . . See also [1] in the Stony Brook Algorithm Repository.
Alexander Soifer. The Mathematical Coloring Book. - Springer-Verlag, 2008 .-- ISBN 978-0-387-74640-1 .
PG Tait. Remarks on the colors of maps // Proc. R. Soc. Edinburgh. - 1880. - T. 10 . - S. 729 .
Trahtman. The road coloring problem // Israel Journal of Mathematics. - 2009.- T. 172 , no. 1 . - S. 51-60 . - DOI : 10.1007 / s11856-009-0062-5 . - arXiv : 0709.0099 .
VG Vizing. On an estimate of the chromatic class of a p -graph // Diskret. Analiz .. - 1964. - T. 3 . - S. 25-30 .
VG Vizing. Critical graphs with given chromatic class // Metody Diskret. Analiz .. - 1965. - T. 5 . - S. 9-17 . . (In Russian.)
DP Williamson, LA Hall, JA Hoogeveen, CAJ Hurkens, JK Lenstra, SV Sevast'janov, DB Shmoys. Short shop schedules // Operations Research. - 1997. - T. 45 , no. 2 . - S. 288-294 . - DOI : 10.1287 / opre.45.2.288 .
Xiao Zhou, Shin-ichi Nakano, Takao Nishizeki. Edge-coloring partial $k$ ${\ displaystyle k}$ -trees // Journal of Algorithms. - 1996. - T. 21 , no. 3 . - S. 598-617 . - DOI : 10.1006 / jagm.1996.0061 .

↑ ¹ ² Chen, Yu, Zang, 2011 .

[_9ed9e1c121c7530c-1] Soifer, 2008 , problem 16.4, p. 133.

[_031838408401dfa9-2] Soifer, 2008 .

[3] Soifer, 2008 , Problem 16.5, p. 133. The fact that you need either $n$ ${\ displaystyle n}$ either $(n-1)$ ${\ displaystyle (n-1)}$ colors follows from Wiesing's theorem .

[_3a8d7934bc5a6a48-4] Biggs, 1972 .

[5] Biggs, 1972 ; Meredith, Lloyd, 1973 ; Bigs, 1979 .

[_b21217417e77e173-6] ¹ ² Soifer, 2008 , p. 134.

[_79629b92e9ff07b0-7] ¹ ² König, 1916 .

[_0f5c1afd86dd3933-8] Erdös, Wilson, 1977 .

[9] Holler, 1981 .

[_64f40409428227c1-10] Wiesing, 1965 .

[_db9fea4ef663382f-11] Sanders, Zhao, 2001 .

[12] Tight, 1880 ; Appel, Haken, 1976 .

[_b21217417e77e171-13] Soifer, 2008 , p. 136.

[_1e0b4e6c98ff9d2c-14] Shannon, 1949 .

[_641064f330c6d6d4-15] ¹ ² Cole, Ost, Shirra, 2001 .

[_a75c3ccc6ae4be13-16] Cole, Hopcroft, 1982 .

[_c16e7778680d5224-17] Alon, 2003 .

[_9ef174f7369e49c3-18] Gabrov, 1976 .

[_39c501a8f9b9e92b-19] Cole, Kovalik, 2008 .

[_88b5f9ff082780b0-20] Misra, Grize, 1992 .

[_16bc9fa39964640c-21] Gabrov et al., 1985 .

[_db4a047bbc256a1e-22] Carlof, Schmoys, 1987 .

[_d3026e7af82c5747-23] Bar Noi, Motwani, Naor, 1992 .

[_35f63b5afb4b35ec-24] Bahmani, Mehta, Motwani, 2010 .

[25] Goldberg, 1973 , Andersen, 1977 ; Seymour, 1979 .

[_7558a03458fa8da1-26] Chen, Yu, Zang, 2011 .

[_8c0601de26dd5f87-27] Kovalik, 2009 .

[_a4eb670af9b38578-28] ¹ ² Epstein, 2008 .

[_ec618d0506cb2072-29] Björklund, Husfeld, Koivisto, 2009 .

[_568eb53c6d121511-30] Zhou, Nakano, Nishiseki, 1996 .

[_3c8d99f02678cf5e-31] Nemhauser, Park, 1991 .

[_98599a3191e613b2-32] Schwenk, 1989 .

[_8b6c7500e81f3258-33] Folkman, Fulkerson, 1969 .

[_584e704ad25f1415-34] Bosak, 1972 .

[_dd7abade81601526-35] Richter, 2011 .

[36] Akiyama, Ikzu, Harari, 1980 , Habib, Peroshe, 1982 , Horak, Nipel, 1982 .

[_fb198e88d9f3600e-37] Nash-Williams, 1964 .

[_ba1ae1dad0c375b8-38] Gabrov, Westerman, 1992 .

[_315160e326442b2c-39] Galvin, 1995 .

[_7285b69d6b54bfbc-40] Bosak, Neschetril, 1976 .

[41] Fouquet, Jolive, 1983 ; Mahdian, 2002 ; Frieze, Krivelevich, Sudakov, 2005 ; Cranston, 2006 .

[_c7dd10475ae974d7-42] Barrett et al., 2006 .

[43] Alon, Sudakov, Sax, 2001 , Muthu, Narayanan, Subramanyan, 2007 .

[_fa2ed53b5dc991e7-44] Epstein, 2010 .

[_3650ce8ccdc26a0d-45] Burke, Verra, Kingston, 2004 .

[_a64f86feee590b6e-46] Skien, 2008 .

[_dc1e9b3d7c43a473-47] Williamson et al., 1997 .

[_4cbfe7d980c7ca47-48] Gandham, Dawanda, Prakash, 2005 .

[_8a95cdd674dc0fae-49] Elebach, Jensen, 2001 .

[_34c2ae1b7fd8aae2-50] Jensen, Toft, 1995 .

[_ff425bd7775bfe83-51] Goldberg, 1973 .

[Edge-Colouring_Eight-Regular_Planar_Graphs-52] Maria Chudnovsky, Katherine Edwards, Paul Seymour. Edge-coloring eight-regular planar graphs (neopr.) . - 2012 .-- 13 January.

[_7558a03458fa8da1-53] ¹ ² Chen, Yu, Zang, 2011 .