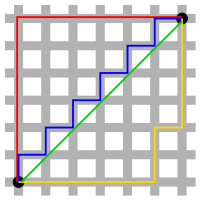
City blocks distance

In the metric of city blocks, the lengths of red, yellow, and blue lines are equal (12). In Euclidean geometry, the green line has a length of 6√2 ≈ 8.49 and is the only shortest path.

City block distance is a metric introduced by German Minkowski . According to this metric, the distance between two points is equal to the sum of the absolute values of the differences of their coordinates.

This metric has many names. City block distance is also known as Manhattan distance , a rectangular city metric, L1 metric or norm $\ell _{1}$ ${\ displaystyle \ ell _ {1}}$ $\ ell _ {1}$ (see space L ^p ), city block metric, taxi metric, Manhattan metric , rectangular metric , right angle metric ; on $\mathbb {Z} ^{2}$ ${\ displaystyle \ mathbb {Z} ^ {2}}$ $\ mathbb {Z} ^ {2}$ it is called the grid metric and the 4-metric ^[1] ^[2] ^[3] .

The name "Manhattan distance" is associated with the street layout of Manhattan ^[4] .

Circles in discrete and continuous geometry of city blocks

Formal Definition

City blocks distance $d_{1}$ ${\ displaystyle d_ {1}}$ $d_{1}$ between two vectors $\mathbf {p} ,\mathbf {q}$ ${\ displaystyle \ mathbf {p}, \ mathbf {q}}$ $\mathbf {p} ,\mathbf {q}$ in an n- dimensional real vector space with a given coordinate system , the sum of the lengths of the projections of the segment between points on the coordinate axis. More formally,

d_{1}(\mathbf {p} ,\mathbf {q} )=\|\mathbf {p} -\mathbf {q} \|_{1}=\sum _{i=1}^{n}|p_{i}-q_{i}|,

{\ displaystyle d_ {1} (\ mathbf {p}, \ mathbf {q}) = \ | \ mathbf {p} - \ mathbf {q} \ | _ {1} = \ sum _ {i = 1} ^ {n} | p_ {i} -q_ {i} |,}

d_{1}(\mathbf {p} ,\mathbf {q} )=\|\mathbf {p} -\mathbf {q} \|_{1}=\sum _{i=1}^{n}|p_{i}-q_{i}|,

Where

\mathbf {p} =(p_{1},p_{2},\dots ,p_{n})

{\ displaystyle \ mathbf {p} = (p_ {1}, p_ {2}, \ dots, p_ {n})}

\mathbf {p} =(p_{1},p_{2},\dots ,p_{n})

and

\mathbf {q} =(q_{1},q_{2},\dots ,q_{n})

{\ displaystyle \ mathbf {q} = (q_ {1}, q_ {2}, \ dots, q_ {n})}

{\mathbf {q}}=(q_{1},q_{2},\dots ,q_{n})

- vectors .

For example, on a plane, the distance of city blocks between $(p_{1},p_{2})$ ${\ displaystyle (p_ {1}, p_ {2})}$ $(p_{1},p_{2})$ and $(q_{1},q_{2})$ ${\ displaystyle (q_ {1}, q_ {2})}$ $(q_{1},q_{2})$ equally $|p_{1}-q_{1}|+|p_{2}-q_{2}|.$ ${\ displaystyle | p_ {1} -q_ {1} | + | p_ {2} -q_ {2} |.}$ $|p_{1}-q_{1}|+|p_{2}-q_{2}|.$

Properties

The Manhattan distance depends on the rotation of the coordinate system, but does not depend on reflection relative to the coordinate axis or transport . In the geometry based on the Manhattan distance, all Hilbert's axioms are fulfilled , except for the axiom of congruent triangles.

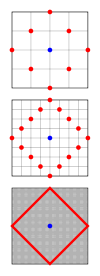
For three-dimensional space, the ball in this metric has the shape of an octahedron , whose vertices lie on the coordinate axes.

Examples

	a	b	c	d	e	f	g	h
eight									eight
7									7
6									6
five									five
four									four
3									3
2									2
one									one
	a	b	c	d	e	f	g	h

The Manhattan distance between two fields of a chessboard is equal to the minimum number of moves that the vizier needs to move from one field to another.

Chess Distances

The distance between the fields of the checkerboard for the vizier (or rook , if the distance is counted in cells) is equal to the Manhattan distance; the king uses the Chebyshev distance , and the elephant uses the Manhattan distance on the board rotated 45 °.

Fifteen

The sum of the Manhattan distances between the knuckles and the positions in which they are located in the solved “ Fifteen ” puzzle is used as a heuristic function to find the optimal solution ^[5] .

Cellular Automata

The set of cells on a two-dimensional square parquet , the Manhattan distance to which from this cell does not exceed r , is called the von Neumann neighborhood of the range (radius) r ^[6] .

Notes

↑ Elena Deza, Michelle Marie Desa. Chapter 19. Distances on the real and digital planes. 19.1. Metrics on the Real Plane // Encyclopedic Dictionary of Distances = Dictionary of Distances. - M: Nauka, 2008 .-- S. 276. - ISBN 978-5-02-036043-3 .
↑ Cluster Analysis: Distance Measures
↑ Manhattan distance
↑ City Block Distance. Spotfire Technology Network.
↑ Computer History: Heuristic Functions
↑ Weisstein, Eric W. von Neumann Neighborhood on Wolfram MathWorld .

Literature

Eugene F. Krause. Taxicab Geometry. - Dover, 1987 .-- ISBN 0-486-25202-7 .

Links

city-block metric on PlanetMath
Weisstein, Eric W. Taxicab Metric ( Wolfram ) at Wolfram MathWorld .
Manhattan distance . Paul E. Black, Dictionary of Algorithms and Data Structures , NIST
Taxi! - AMS column about Taxicab geometry
TaxicabGeometry.net - a website dedicated to taxicab geometry research and information

[1] Elena Deza, Michelle Marie Desa. Chapter 19. Distances on the real and digital planes. 19.1. Metrics on the Real Plane // Encyclopedic Dictionary of Distances = Dictionary of Distances. - M: Nauka, 2008 .-- S. 276. - ISBN 978-5-02-036043-3 .

[2] Cluster Analysis: Distance Measures

[3] Manhattan distance

[4] City Block Distance. Spotfire Technology Network.

[5] Computer History: Heuristic Functions

[6] Weisstein, Eric W. von Neumann Neighborhood on Wolfram MathWorld .