In cryptography , a sponge function (or just a sponge ) ( English sponge construction or sponge function ) is a class of algorithms with a finite internal state, whose input is a binary string of arbitrary length, and which return a binary string of arbitrary length f : {0,1} n → {0,1} * . The sponge function can be used to create hash functions , stream and block ciphers, and pseudo-random number generators having an arbitrary length of input data.
Content
Structure
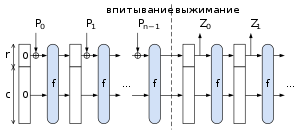
A sponge is an iterative construct for creating a function with an arbitrary length at the input and an arbitrary length at the output based on the transformations f. The sponge has an internal state S - with data of a fixed size b (bit). The data are divided into 2 parts - the first S1 of size r, and the second S2 - of size c. The value of r is called the bit rate, and the value of c is the power; b = r + c.
In the initialization phase, the data block of size b is filled with zeros, and the input data M is divided into blocks of size r. Further work sponge is made in 2 stages:
- In the “absorbing” phase, the XOR operation of the next block of the original message is performed with the first part of state S1 of size r (bit), the remaining part of state S2 with capacity c remains unaffected. The result is placed in S1, and then the state S is processed by the function f, a multi-round keyless pseudo-random permutation, and this is repeated until the original message blocks are exhausted.
- In the “squeezing” phase, the state S is fed to the function f, after which part S1 is fed to the output. These actions are repeated until a sequence of the desired length is obtained (for example, the length of the hash).
The last bits of c depend on input blocks only indirectly and are not output during the “squeezing” phase.
Application
Pseudo-random number generator based on sponge function
PRNG simulation with variable input
We define the PRNG with variable input data as an object with a state that supports two types of queries, in any order:
- Feed request, feed (σ) - gives an initial value consisting of a non-empty string σ in the state of PRNG;
- Accept request, fetch (l) - instructs the PRNG to return l bits.
Then the source material (seeding material) fed to the input of the generator is the concatenation of σ received in all the feed requests.
Informally, the PRNG requirements with variable source data can be defined as follows:
First, its output (i.e. responses to requests for submission) must depend on all the source materials. Secondly, for an attacker who does not know the source material, but who observed part of the output, it should be impossible to conclude about the remainder of the output.
We define the ideal PRNG as a construction using a random oracle.
The construction that we defined can be described as follows. She saves as a state the sequence of all the requests for submission and acceptance she received, making up history h. When it receives a feed (σ) feed request, it updates the history by connecting this query. When it receives a fetch (l) request, it sends a random oracle a string, which in turn encrypts history with a string and returns bits from z to z + l-1 of its response, where z is the number of requested bits in the feed request. Consequently, the concatenation of responses to filing requests is only the response of a random oracle to a single query. This is illustrated in the figure. We call this construction the history saving mode with the encryption function e (h). The definition of the mode with preservation of history, therefore, converges to the definition of this encryption function.
Since the PRNG output should depend on the total source material obtained, the encryption function e (h) must be injective with the source material. In other words, for any two query sequences with different source material, the two e (h) mappings should be different. We call this the completeness of the source material (seed-completeness). In the encryption function with full source material, the acceptance request will be given various responses to different input lines. It follows that the PRNG returns independent bits.
Thus, the following definition of an ideal PRNG with variable input data is proposed.
An ideal PRNG with variable input data is a history-saving mode, called a random oracle, with the e (h) encryption function with full source material.
Creating the PRNG using the sponge function
It seems natural to include a feed request in the “soak” phase, and a request for acceptance in the “squeeze” phase. However, the execution of the sponge function has only one absorption phase (one input), followed by a single “squeezing” phase (i.e. one output of arbitrary length) and it cannot be used to produce multiple phases.
Obviously, this difficulty is easily circumvented. It is enough to assume that every time pseudo-random bits are received, another execution of the sponge function is requested with a different input.
When building a sponge function, the input message is m ϵ must be divided into blocks of r bits and filled. Let p (m) be the function that does this and assume that this function adds only bits after m. Suppose we want to reuse the state of the sponge, for which the input string was the message m1 and for which the output bits were “squeezed out” when l> 0. The state of the sponge function at this point is as if the partial message m'1 = p (m1) || 0 r (⌈l / r⌉-1) was “absorbed.” Note that zero blocks are additional iterations due to the compression phase. Restarting the sponge from this point means that the input will be the message m2, for which m'1 is a prefix one.
To formally define the PRNG, we need to specify the encryption function e (h) with the complete source material, which represents the sequence of requests for submission and acceptance. Output e (h) is used as input for the sponge function.
In practice, the idea is not to call the sponge function with the whole e (h) every time we receive an acceptance request. Instead, the design uses the sponge function in a cascaded manner, reusing the state as described in section 3.2. [ where? ] To allow reuse of the state of the sponge function, e (h) should be such that if h '= h || fetch (l) || feed (σ), then p (e (h)) || 0 r (⌈l / r⌉-1) is the prefix e (h ').
To associate a structure with practical implementation, we first describe a structure with two constraints. The first limit is on the length of the queries of the original value. For a fixed integer k, we require that the source material σ in any feed request feed (σ) be such that | p (σ) | = kr. In other words, after filling, the source material covers exactly k blocks of r bits each. The second limitation is that the first request should be a request for submission.
A construct is a stateful construct if its state consists of mϵ N bits received since the last filing request. Let's start with the new version of the sponge function, set m = 0. Denote as e line, display e (h) of queries added to history h.
- If the fetch (l) request came:
Execution produces l output bits, “squeezing” them out of the function of the sponge. Formally, it will be adapted at the time of the next filing request.
The value of m is changed: m = m + l.
- If the request came feed (σ):
Formally, this filing request triggers a request to a jaw function with e as input. If this is not the first request, then it is not updated until the last submission request. Thus, the results of receiving requests from the time of the last filing request should be included in the e, as if it had previously been absorbed. At first, e becomes equal to p (e) to simulate the filling when switching to the “squeezing” phase after the previous feed request. Then the ⌈m \ r⌉ −1 blocks of r zeroes are added to e to account for additional calls to the function f in subsequent feed requests. Now m is reset: m = 0. (This part only affects e - nothing should change in execution).
Then σ is absorbed. Formally, this is expressed by adding σ to e.
Finally, execution switches the function of the sponge to the “squeeze” phase. This means that the “absorbed” data must be filled in and the permutation f applied to the state. (Formally, this does not change e, since the filling, by definition, is performed when switching to the spin phase).
The restriction on the fixed size of filing requests is optional and can be removed. To ensure the variable length of the source material and preserve the completeness of the source material, some filling forms must be entered within the encryption function to ensure that the boundaries of the source material can be identified. In addition, you will have to add a way to distinguish blocks with zero source material from zero blocks. This can be done, for example, by setting 1 into each block containing the source material.
The restriction of the first request, which is a feed request, can be removed, since it does not make sense to generate pseudo-random bits without first feeding the source material. If the first request is acceptance, then execution immediately fills in (empty line) the input, switches the sponge functions to the “squeezing” phase and produces output bits using “squeezing”. Formally, in the next filing request, this must be taken into account in e by assigning e to the value of p (empty line) || 0 r ([m = r] -1) .
Algorithm implementations
- Keccak
- Luffa