Multidimensional time

Properties of S + T- dimensional space-time

Multidimensional time — hypotheses for the existence of time with dimension T > 1. These hypotheses have a certain distribution in physics , philosophy, and science fiction .

In Physics

The special theory of relativity (STR) describes space-time in the form of a pseudo-Riemannian manifold with one negative eigenvalue of the metric tensor , which corresponds to a “time-like” direction. A metric with several negative eigenvalues will accordingly imply the presence of several time directions, that is, time will be multidimensional, but there is currently no consensus about the relationship of these additional “times” with time in the usual sense.

The hypotheses of multidimensional time have been put forward in physics in two ways: as a possible theoretical description of reality or as a curious opportunity, probably not related to the known nature. For example, Yitzhak Bars published the work “Physics of two-dimensional time” ^[1] , based on the symmetry SO (10, 2) of the extended structure of the supersymmetry of M-theory , which is the most modern and systematized version of this theory (see also F-theory ).

If the special theory of relativity can be generalized to the case of k -dimensional time ( t ₁ , t ₂ , ..., t _k ) and n -dimensional space ( x _{k +1} , x _{k +2} , ..., x k + n ), then the ( k + n ) -dimensional interval, being invariant, gives the expression (d s _{k , n} ) ² = ( c d t ₁ ) ² + ... + ( c d t _k ) ² - (d x _{k +1} ) ² - ... - (d x _{k + n} ) ² . The metric signature will then look like this:

(\underbrace {+,\cdots ,+} _{k},\underbrace {-,\cdots ,-} _{n})

{\ displaystyle (\ underbrace {+, \ cdots, +} _ {k}, \ underbrace {-, \ cdots, -} _ {n})}

(\underbrace {+,\cdots ,+} _{k},\underbrace {-,\cdots ,-} _{n})

- temporary-like rule of signs ,

or

(\underbrace {-,\cdots ,-} _{k},\underbrace {+,\cdots ,+} _{n})

{\ displaystyle (\ underbrace {-, \ cdots, -} _ {k}, \ underbrace {+, \ cdots, +} _ {n})}

(\underbrace {-,\cdots ,-} _{k},\underbrace {+,\cdots ,+} _{n})

- a spatially similar sign rule .

Transformations between two inertial reference frames K and K ′, which are in the standard configuration (for example, a transformation without translation and / or rotation of the space axis in a hyperplane of space and / or rotations of the time axis in a time hyperplane) look as follows ^[2] :

t'_{\sigma }=\sum _{\theta =1}^{k}\left(\delta _{\sigma \theta }t_{\theta }+{\frac {c^{2}}{v_{\sigma }v_{\theta }}}\beta ^{2}(\zeta -1)t_{\theta }\right)-{\frac {1}{v_{\sigma }}}\beta ^{2}\zeta x_{k+1},

{\ displaystyle t '_ {\ sigma} = \ sum _ {\ theta = 1} ^ {k} \ left (\ delta _ {\ sigma \ theta} t _ {\ theta} + {\ frac {c ^ {2 }} {v _ {\ sigma} v _ {\ theta}}} \ beta ^ {2} (\ zeta -1) t _ {\ theta} \ right) - {\ frac {1} {v _ {\ sigma}}} \ beta ^ {2} \ zeta x_ {k + 1},}

x'_{k+1}=-c^{2}\beta ^{2}\zeta \sum _{\theta =1}^{k}{\frac {t_{\theta }}{v_{\theta }}}+\zeta x_{k+1},

{\ displaystyle x '_ {k + 1} = - c ^ {2} \ beta ^ {2} \ zeta \ sum _ {\ theta = 1} ^ {k} {\ frac {t _ {\ theta}} { v _ {\ theta}}} + \ zeta x_ {k + 1},}

x'_{\lambda }=x_{\lambda },

{\ displaystyle x '_ {\ lambda} = x _ {\ lambda},}

Where $\mathbf {v} _{1}=(v_{1},\underbrace {0,\cdots ,0} _{n-1}),$ ${\ displaystyle \ mathbf {v} _ {1} = (v_ {1}, \ underbrace {0, \ cdots, 0} _ {n-1}),}$ $\mathbf {v} _{2}=(v_{2},\underbrace {0,\cdots ,0} _{n-1}),$ ${\ displaystyle \ mathbf {v} _ {2} = (v_ {2}, \ underbrace {0, \ cdots, 0} _ {n-1}),}$ $\mathbf {v} _{k}=(v_{k},\underbrace {0,\cdots ,0} _{n-1})$ ${\ displaystyle \ mathbf {v} _ {k} = (v_ {k}, \ underbrace {0, \ cdots, 0} _ {n-1})}$ are the velocity vectors K ′ against K , respectively, depending on the size of the time t ₁ , t ₂ , ..., t _k ; $\beta ={\frac {1}{\sqrt {\sum _{\mu =1}^{k}{\frac {c^{2}}{v_{\mu }^{2}}}}}};$ ${\ displaystyle \ beta = {\ frac {1} {\ sqrt {\ sum _ {\ mu = 1} ^ {k} {\ frac {c ^ {2}} {v _ {\ mu} ^ {2}} }}}};}$ $\zeta ={\frac {1}{\sqrt {1-\beta ^{2}}}};$ ${\ displaystyle \ zeta = {\ frac {1} {\ sqrt {1- \ beta ^ {2}}}};}$ σ = 1, 2, ..., k ; λ = k + 2, k + 3, ..., k + n . Here δ _σθ is the Kronecker symbol . These transformations are a generalization of the Lorentz transform in a fixed spatial direction ( x _{k +1} ) in the field of multidimensional time and multidimensional space.

Causal structure of space-time with two time dimensions and one dimension of space

Denote: ${\frac {dx_{\eta }}{dt_{\sigma }}}=V_{\sigma \eta }$ ${\ displaystyle {\ frac {dx _ {\ eta}} {dt _ {\ sigma}}} = V _ {\ sigma \ eta}}$ , and ${\frac {dx'_{\eta }}{dt'_{\sigma }}}=V'_{\sigma \eta },$ ${\ displaystyle {\ frac {dx '_ {\ eta}} {dt' _ {\ sigma}}} = V '_ {\ sigma \ eta},}$ where σ = 1, 2, ..., k ; η = k + 1, k + 2, ..., k + n . Addition of speeds will then give

V'_{\sigma (k+1)}={\frac {V_{\sigma (k+1)}\zeta \left(1-\beta ^{2}\sum _{\theta =1}^{k}{\frac {c^{2}}{v_{\theta }V_{\theta (k+1)}}}\right)}{1+{\frac {V_{\sigma (k+1)}}{v_{\sigma }}}\beta ^{2}\left((\zeta -1)\sum _{\theta =1}^{k}{\frac {c^{2}}{v_{\theta }V_{\theta (k+1)}}}-\zeta \right)}},

{\ displaystyle V '_ {\ sigma (k + 1)} = {\ frac {V _ {\ sigma (k + 1)} \ zeta \ left (1- \ beta ^ {2} \ sum _ {\ theta = 1} ^ {k} {\ frac {c ^ {2}} {v _ {\ theta} V _ {\ theta (k + 1)}}} \ right)} {1 + {\ frac {V _ {\ sigma ( k + 1)}} {v _ {\ sigma}}} \ beta ^ {2} \ left ((\ zeta -1) \ sum _ {\ theta = 1} ^ {k} {\ frac {c ^ {2 }} {v _ {\ theta} V _ {\ theta (k + 1)}}} - \ zeta \ right)}},}

V'_{\sigma \lambda }={\frac {V_{\sigma \lambda }}{1+{\frac {V_{\sigma (k+1)}}{v_{\sigma }}}\beta ^{2}\left((\zeta -1)\sum _{\theta =1}^{k}{\frac {c^{2}}{v_{\theta }V_{\theta (k+1)}}}-\zeta \right)}},

{\ displaystyle V '_ {\ sigma \ lambda} = {\ frac {V _ {\ sigma \ lambda}} {1 + {\ frac {V _ {\ sigma (k + 1)}} {v _ {\ sigma}} } \ beta ^ {2} \ left ((\ zeta -1) \ sum _ {\ theta = 1} ^ {k} {\ frac {c ^ {2}} {v _ {\ theta} V _ {\ theta ( k + 1)}}} - \ zeta \ right)}},}

where σ = 1, 2, ..., k ; λ = k + 2, k + 3, ..., k + n .

For simplicity, we consider only one spatial dimension x ₃ and two temporal dimensions x ₁ and x ₂ (that is, x ₁ = ct ₁ , x ₂ = ct ₂ , x ₃ = x ). Suppose that at point O having coordinates x ₁ = 0, x ₂ = 0, x ₃ = 0, event E took place. Further suppose that a given time interval $\Delta T={\sqrt {(\Delta t_{1})^{2}+(\Delta t_{2})^{2}}}\geqslant 0$ ${\ displaystyle \ Delta T = {\ sqrt {(\ Delta t_ {1}) ^ {2} + (\ Delta t_ {2}) ^ {2}}} \ geqslant 0}$ passed since the event E. The causal area associated with event E includes the lateral surface of a straight circular cone {( x ₁ ) ² + ( x ₂ ) ² - ( x ₃ ) ² = 0}, the lateral surface of a straight circular cylinder {( x ₁ ) ² + ( x ₂ ) ² = c ² Δ T ² } and the inner region bounded by these surfaces, that is, the causal region includes all points ( x ₁ , x ₂ , x ₃ ) for which the conditions

{( x ₁ ) ² + ( x ₂ ) ² - ( x ₃ ) ² = 0 and | x ₃ | ⩽ c Δ T } or

{( x ₁ ) ² + ( x ₂ ) ² = c ² Δ T ² and | x ₃ | ⩽ c Δ T } or

{( x ₁ ) ² + ( x ₂ ) ² - ( x ₃ ) ² > 0 and ( x ₁ ) ² + ( x ₂ ) ² < c ² Δ T ² }

are fulfilled ^[3] .

Nevertheless, signatures (1, 3) and (3, 1) are physically equivalent, since the positive length of a vector in Minkowski space for timelike intervals is a convention depending on the agreement on the sign of the metric tensor ^[4] . So, some physicists usually use a metric with a signature (+ −−−), which leads to a positive Minkowski “length” for time-like intervals and energy, while the spatial distance will have a negative Minkowski “length”. Relativists, however, tend to adhere to the opposite convention (- +++), which gives a positive "length" of Minkowski for spatial distance .

All universes of multidimensional time can be considered as freedmons ^[5] .

Relationship with the Anthropic Principle

As evidence of the three-dimensionality of space (apart from the possible measurements of an unconfirmed string theory ), the physical consequences of the assumption that the number of measurements differs from three spatial plus one temporal can be given. This argument is made in the spirit of the anthropic principle, and perhaps this is the first case of its use, albeit before the concept of this principle was fully formulated

The implicit idea that the dimension of the existing Universe is special was first expressed by Leibniz , who in his “Reasoning on Metaphysics” suggested that “the world corresponds to a model that is the simplest in the hypothesis and the richest in phenomena” ^[6] .

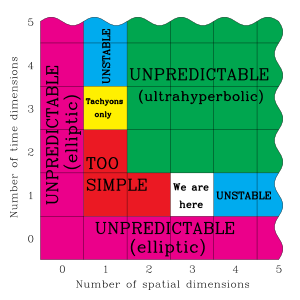
Max Tegmark ^[7] considers the hypotheses of worlds with a dimension of time T > 1 from the point of view of the anthropic principle and comes to the conclusion that the existence of intelligent life in such a model of the world is impossible. In the general case, the functioning of physical laws in a world with multidimensional time is unknown. If T is different from 1, the behavior of physical systems cannot be deduced from knowledge of the corresponding partial differential equations - the Cauchy problem for the wave equation becomes poorly defined. In other words, in a world with multidimensional time, it is impossible to accurately calculate the behavior of physical systems in the future, and any calculation of physical laws will have several solutions - the future of such a universe cannot be predicted. Intelligent life, capable of using technology, in such a universe could not have arisen. Moreover, Tegmark argues that if T > 1, protons and electrons would be unstable and could decay into more massive particles. (This is not a problem if the particles have a sufficiently low temperature.) At T > 1, subatomic particles decaying over a certain period would behave unpredictably, the geodesic line would not necessarily be maximum for time. The case of the world with the dimension of space N = 1 and time T = 3 has an interesting property: the speed of light is the lower boundary of the speed of material bodies, and all matter consists of tachyons .

Only in a world with one-dimensional time can one reliably calculate the state of physical systems in the future (in a world without time, such calculations are impossible, but in a world with multi-dimensional time, calculating the future state of physical systems provides several solutions). The only option for one solution for physical equations in a world with multidimensional time is the movement of the observer at the speed of light, when time does not exist for him at all. Only a world with three-dimensional space gives sufficient stability and complexity, since in a world with a number of dimensions of space less than 3 gravity is unlikely and topological problems arise, and in a world with a number of dimensions of space more than 3, stable orbits cannot exist (for gravitational and electromagnetic fields or other long-range interactions). Therefore, worlds with a time dimension other than 1 have a lack of predictability, and worlds with an expanded dimensionality of space greater than 3 have a lack of stability. Thus, observance of the anthropic principle excludes any variants of the world besides N = 3 and T = 1 (or N = 1 and T = 3 in other concepts) ^[7] .

Relationship with Planck length and speed of light

The motion of the test particle can be described by the coordinate:

$x^{\mu }={\begin{pmatrix}ct\\r\cdot f\left({\frac {\gamma \tau }{\Lambda }}\right)\\\mathbf {x} \end{pmatrix}}$ ${\ displaystyle x ^ {\ mu} = {\ begin {pmatrix} ct \\ r \ cdot f \ left ({\ frac {\ gamma \ tau} {\ Lambda}} \ right) \\\ mathbf {x} \ end {pmatrix}}}$

which is the canonical (1,3) space-time vector $(ct,\mathbf {x} )^{T}$ ${\ displaystyle (ct, \ mathbf {x}) ^ {T}}$ with $x\in \mathbb {R} ^{3}$ ${\ displaystyle x \ in \ mathbb {R} ^ {3}}$ extended to an additional time-like coordinate $r\cdot f(\gamma \tau /\Lambda )$ ${\ displaystyle r \ cdot f (\ gamma \ tau / \ Lambda)}$ . $\tau$ ${\ displaystyle \ tau}$ then the second parameter of time, $r\in \mathbb {R}$ ${\ displaystyle r \ in \ mathbb {R}}$ describes the size of the second time dimension and $\gamma$ ${\ displaystyle \ gamma}$ is the characteristic speed, so the equivalent $c$ ${\ displaystyle c}$ . $f$ ${\ displaystyle f}$ describes the shape of the second time dimension and $\Lambda \in \mathbb {R}$ ${\ displaystyle \ Lambda \ in \ mathbb {R}}$ normalization parameter such that $\gamma \tau /\Lambda$ ${\ displaystyle \ gamma \ tau / \ Lambda}$ dimensionless. Breaking up $x^{\mu }=x_{t}^{\mu }+x_{\tau }^{\mu }$ ${\ displaystyle x ^ {\ mu} = x_ {t} ^ {\ mu} + x _ {\ tau} ^ {\ mu}}$ with

$x_{t}^{\mu }={\begin{pmatrix}ct\\0\\\eta \mathbf {x} \end{pmatrix}};\ x_{\tau }^{\mu }={\begin{pmatrix}0\\r\cdot f\left({\frac {\gamma \tau }{\Lambda }}\right)\\(1-\eta )\mathbf {x} \end{pmatrix}},\eta \in (0,1)$ ${\ displaystyle x_ {t} ^ {\ mu} = {\ begin {pmatrix} ct \\ 0 \\\ eta \ mathbf {x} \ end {pmatrix}}; \ x _ {\ tau} ^ {\ mu} = {\ begin {pmatrix} 0 \\ r \ cdot f \ left ({\ frac {\ gamma \ tau} {\ Lambda}} \ right) \\ (1- \ eta) \ mathbf {x} \ end { pmatrix}}, \ eta \ in (0,1)}$

and using the metric $(+,+,-,-,-)$ ${\ displaystyle (+, +, -, -, -)}$ then Lagrange mechanics becomes

$L(x,{\dot {x}},x^{\prime },t,\tau )={\frac {r}{\Lambda }}{\sqrt {{\dot {c}}^{2}t^{2}+c^{2}-\eta ^{2}{\dot {\mathbf {x} }}^{2}+2{\dot {c}}ct}}{\sqrt {(\gamma ^{\prime 2}\tau ^{2}+\gamma ^{2}+2\gamma \gamma ^{\prime }\tau )\left(\left.{\frac {df}{dz}}\right|_{z={\frac {\gamma \tau }{\Lambda }}}\right)^{2}-(1-\eta )^{2}\mathbf {x} ^{\prime 2}}}.$ ${\ displaystyle L (x, {\ dot {x}}, x ^ {\ prime}, t, \ tau) = {\ frac {r} {\ Lambda}} {\ sqrt {{\ dot {c}} ^ {2} t ^ {2} + c ^ {2} - \ eta ^ {2} {\ dot {\ mathbf {x}}} ^ {2} +2 {\ dot {c}} ct}} { \ sqrt {(\ gamma ^ {\ prime 2} \ tau ^ {2} + \ gamma ^ {2} +2 \ gamma \ gamma ^ {\ prime} \ tau) \ left (\ left. {\ frac {df } {dz}} \ right | _ {z = {\ frac {\ gamma \ tau} {\ Lambda}}} \ right) ^ {2} - (1- \ eta) ^ {2} \ mathbf {x} ^ {\ prime 2}}}.}$

Application of the Euler - Lagrange equation gives

${\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {x}}_{i}}}+{\frac {d}{d\tau }}{\frac {\partial L}{\partial x_{i}^{\prime \ }}}-{\frac {\partial L}{\partial x_{i}}}=0$ ${\ displaystyle {\ frac {d} {dt}} {\ frac {\ partial L} {\ partial {\ dot {x}} _ {i}}} + {\ frac {d} {d \ tau}} {\ frac {\ partial L} {\ partial x_ {i} ^ {\ prime \}}} - {\ frac {\ partial L} {\ partial x_ {i}}} = 0}$

As a consequence of this model, it was suggested that the speed of light was not constant in the early Universe ^[8] .

In Philosophy

In 1927, the essay " An Experiment with Time " by John Dunn was published. In this essay, a hypothesis is put forward about the existence of a person at the same time at two levels: in the subjective flow of time (see the arrow of time ) and outside the time axis with the ability to simultaneously see the past, present and future (see eternalism ). In his article “ The Unreality of Time »English philosopher John Ellis McTaggart divides time into two series: A-series and B-series (see Eternalism # John McTaggart's Argumentation ).

The hypothesis of multidimensional time was also considered in analytical philosophy ^[9] .

The English philosopher John Bennett considers a model of the Universe with 6 dimensions: 3 spatial and 3 temporal (having the names “ time ”, “ eternity ” and “hyparxis”). By time, John Bennett understands the usual linear course of events. He refers to hypertime eternity and hyparxis, which have their own properties that are different from time. John Bennett calls eternity cosmological time and timeless time. Hyparxis (from other Greek: ὕπαρξις - existence) is a state of being and acts in the field of quantum processes . The combination of time and eternity makes it possible to create a multivariate cosmology with parallel universes , giving a wide range of possibilities. The existence of such a temporary dimension as hyparxis makes many sci-fi ideas possible: traveling in time , moving between parallel worlds, and moving faster than the speed of light . Although John Bennett’s ideas are quite curious, they are based on the subjective aspects of time perception and do not have a completely scientific basis. The question of measuring these hypothetical time dimensions also remains open.

As a solution to the problem of subjective passage of time, Dunn proposed an endless hierarchy of dimensions of time, populated by a similar hierarchy of levels of consciousness. Dunn suggested that in the context of the “block” space-time modeled by the General Theory of Relativity , a second measurement of time is necessary in order to measure the speed of its progress on its own time scale. This in turn required a level of conscious self existing on the second level of time. But the same arguments were then applied to this new level, requiring a third level, and so on in infinite regress . At the end of the regression, there was an “excellent general observer” that existed in eternity ^[10] . He published his theory of subliminal dreams in his 1927 book, An Experiment with Time, and continued to explore its relation to modern physics in the Serial Universe (1934). Its endless regression was criticized as logically erroneous and unnecessary, although authors such as Priestley recognized the possibility of its second time dimension ^[11] ^[12] .

In fiction

In the final novel of the trilogy People as Gods, “The Ring of the Return Time” (1977), Sergei Snegov puts the words in the mouth of the protagonist: “This is my idea - to break out of one-dimensional, rectilinear time during two-dimensional ...” ^[13]
In Robert Heinlein 's novel The Number of the Beast (1979), the Universe has 6 dimensions, including 3 time dimensions (denoted by t, τ (tau) and t).
In Diana Dwayne 's Wounded Sky (1983) Star Trek series, physicist Hamalki K't'lk claims that time has 3 dimensions (“beginning”, “continuation” and “end”).
In the tetralogy “Provision” ( Eng. Ware ) (2000) by Rudy Rücker, the alien metamarsian race originates from the space region with two-dimensional time ^[14] .
In the Sonic the Hedgehog comic book series, the theory of multidimensional time is used to explain the meeting of the main character Sonic with his evil twin Scourge.

Notes

↑ Two-Time Physics (Neopr.) . Date of treatment December 8, 2012. Archived on February 5, 2013.
↑ Velev, Milen. Relativistic mechanics in multiple time dimensions (English) // Physics Essays : journal. - 2012. - Vol. 25 , no. 3 . - P. 403-438 . - DOI : 10.4006 / 0836-1398-25.3.403 . - .
↑ Velev, Milen. Relativistic mechanics in multiple time dimensions (English) // Physics Essays : journal. - 2012. - Vol. 25 , no. 3 . - P. 403-438 . - DOI : 10.4006 / 0836-1398-25.3.403 . - .
↑ Sing, J. L. General Theory of Relativity. - M .: IL, 1963 .-- S. 349.
↑ The geometry of black and white holes (Part 1) .
↑ Leibniz, Gottfried. Discourse on Metaphysics // Die philosophischen schriften von Gottfried Wilhelm Leibniz, Volume 4. - Weidmann, 1880. - P. 427-463.
↑ ¹ ² Tegmark, Max . On the dimensionality of spacetime (English) // Classical and Quantum Gravity : journal. - 1997 .-- April ( vol. 14 , no. 4 ). - P. L69 — L75 . - DOI : 10.1088 / 0264-9381 / 14/4/002 . - . - arXiv : gr-qc / 9702052 .
↑ A. Albrecht, J. Magueijo. A Time Varying Speed of Light as a Solution to Cosmological Puzzles. Phys. Rev. D vol. 59 043516 (1999)
↑ Philosophy Faculty Members: Steven Weinstein (neopr.) . Department of Philosophy, University of Waterloo, Canada. Date of treatment December 8, 2012. Archived on February 5, 2013.
↑ John's Book Reviews: An Experiment with Time (Neopr.) (November 15, 2006). Date of treatment December 8, 2012.
↑ JA Gunn; The Problem of Time , Unwin, 1929.
↑ JB Priestley, Man and Time , Aldus, 1964.
↑ Sergey Snegov. Кольцо обратного времени / Сост. и авт. вступ. Art. Е. Брандис, В. Дмитревский. — Л. : Лениздат, 1977. — С. 11—270. — 639 с. - 100,000 copies.
↑ Notes for Realware (неопр.) (25 ноября 2005). Дата обращения 8 декабря 2012. Архивировано 5 февраля 2013 года.

Literature

Введение в философию — М.: Политиздат, 1989. Ч. 2. — С. 85.
Itzhak Bars, Gauge Symmetry in Phase Space, Consequences for Physics and Spacetime . arXiv:1004.0688 [hep-th].
Itzhak Bars, The Standard model as a 2T-physics theory . hep-th/0610187.
Itzhak Bars, John Terning, Extra dimensions in space and time , NY: Springer, Multiversal journeys series, 2010, ISBN 978-0-387-77638-5 . DOI: 10.1007/978-0-387-77638-5.
Steven Weinstein, Multiple Time Dimensions , arXiv:0812.3869 [physics.gen-ph].
Jacob G. Foster, Berndt Muller, Physics With Two Time Dimensions . arXiv:1001.2485 [hep-th].

[1] Two-Time Physics (Neopr.) . Date of treatment December 8, 2012. Archived on February 5, 2013.

[2] Velev, Milen. Relativistic mechanics in multiple time dimensions (English) // Physics Essays : journal. - 2012. - Vol. 25 , no. 3 . - P. 403-438 . - DOI : 10.4006 / 0836-1398-25.3.403 . - .

[3] Velev, Milen. Relativistic mechanics in multiple time dimensions (English) // Physics Essays : journal. - 2012. - Vol. 25 , no. 3 . - P. 403-438 . - DOI : 10.4006 / 0836-1398-25.3.403 . - .

[4] Sing, J. L. General Theory of Relativity. - M .: IL, 1963 .-- S. 349.

[5] The geometry of black and white holes (Part 1) .

[Leibniz1686-6] Leibniz, Gottfried. Discourse on Metaphysics // Die philosophischen schriften von Gottfried Wilhelm Leibniz, Volume 4. - Weidmann, 1880. - P. 427-463.

[tegmark-dim-7] ¹ ² Tegmark, Max . On the dimensionality of spacetime (English) // Classical and Quantum Gravity : journal. - 1997 .-- April ( vol. 14 , no. 4 ). - P. L69 — L75 . - DOI : 10.1088 / 0264-9381 / 14/4/002 . - . - arXiv : gr-qc / 9702052 .

[8] A. Albrecht, J. Magueijo. A Time Varying Speed of Light as a Solution to Cosmological Puzzles. Phys. Rev. D vol. 59 043516 (1999)

[9] Philosophy Faculty Members: Steven Weinstein (neopr.) . Department of Philosophy, University of Waterloo, Canada. Date of treatment December 8, 2012. Archived on February 5, 2013.

[10] John's Book Reviews: An Experiment with Time (Neopr.) (November 15, 2006). Date of treatment December 8, 2012.

[11] JA Gunn; The Problem of Time , Unwin, 1929.

[12] JB Priestley, Man and Time , Aldus, 1964.

[13] Sergey Snegov. Кольцо обратного времени / Сост. и авт. вступ. Art. Е. Брандис, В. Дмитревский. — Л. : Лениздат, 1977. — С. 11—270. — 639 с. - 100,000 copies.

[14] Notes for Realware (неопр.) (25 ноября 2005). Дата обращения 8 декабря 2012. Архивировано 5 февраля 2013 года.