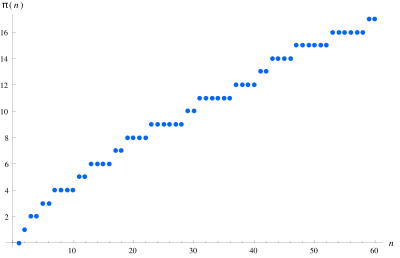
Prime number distribution function

In mathematics , the distribution function of primes or pi-function $\pi (x)$ ${\ displaystyle \ pi (x)}$ $\ pi (x)$ Is a function equal to the number of primes less than or equal to the real number x . ^[1] ^[2] It is designated $\pi (x)$ ${\ displaystyle \ pi (x)}$ $\ pi (x)$ (this has nothing to do with pi ).

The values of the pi-function for the first 60 natural numbers

History

Of great interest in number theory is the growth rate of the pi-function. ^[3] ^[4] At the end of the 18th century, Gauss and Legendre suggested that the pi-function is estimated as

{\frac {x}{\ln x}}

{\ displaystyle {\ frac {x} {\ ln x}}}

{\frac {x}{\ln x}}

in the sense that

\lim \limits _{x\to +\infty }{\frac {\pi (x)}{x/\ln x}}=1.

{\ displaystyle \ lim \ limits _ {x \ to + \ infty} {\ frac {\ pi (x)} {x / \ ln x}} = 1.}

\lim \limits _{{x\to +\infty }}{\frac {\pi (x)}{x/\ln x}}=1.

This statement is a prime number distribution theorem . It is equivalent to the statement

\lim \limits _{x\to +\infty }{\frac {\pi (x)}{\operatorname {li} (x)}}=1

{\ displaystyle \ lim \ limits _ {x \ to + \ infty} {\ frac {\ pi (x)} {\ operatorname {li} (x)}} = 1}

\lim \limits _{{x\to +\infty }}{\frac {\pi (x)}{\operatorname {li}(x)}}=1

Where $\operatorname {li}$ ${\ displaystyle \ operatorname {li}}$ $\operatorname {li}$ Is the integral logarithm . The prime number theorem was first proved in 1896 by Jacques Hadamard and independently Valle-Poussin , using the Riemann zeta function introduced by Riemann in 1859.

More precisely growth $\pi (x)$ ${\ displaystyle \ pi (x)}$ $\pi (x)$ now described as

\pi (x)=\operatorname {li} (x)+O{\bigl (}xe^{-{\sqrt {\ln x}}/15}{\bigr )}

{\ displaystyle \ pi (x) = \ operatorname {li} (x) + O {\ bigl (} xe ^ {- {\ sqrt {\ ln x}} / 15} {\ bigr)}}

\pi (x)=\operatorname {li} (x)+O{\bigl (}xe^{-{\sqrt {\ln x}}/15}{\bigr )}

Where $O$ ${\ displaystyle O}$ $O$ denotes O large . For the most commonly used values of x (that is, when x is not very large) $\operatorname {li} (x)$ ${\ displaystyle \ operatorname {li} (x)}$ $\operatorname {li} (x)$ more than $\pi (x)$ ${\ displaystyle \ pi (x)}$ $\pi (x)$ however the difference $\pi (x)-\operatorname {li} (x)$ ${\ displaystyle \ pi (x) - \ operatorname {li} (x)}$ $\pi (x)-\operatorname {li} (x)$ changes its sign an infinite number of times. See also Skews Number .

Proofs of the prime number theorem that do not use the zeta function or complex analysis were found in 1948 by Atle Selberg and Paul Erdös (mostly independently). ^[five]

Tables for pi function, x / ln x and li ( x )

The following table shows the growth of functions. $\pi (x),{\frac {x}{\ln x}},\operatorname {li} (x)$ ${\ displaystyle \ pi (x), {\ frac {x} {\ ln x}}, \ operatorname {li} (x)}$ by degrees 10 ^[3] ^[6] ^[7] ^[8] .

x	π ( x )	π ( x ) - x / ln x	li ( x ) - π ( x )	x / π ( x )	π ( x ) / x (fraction of primes)
ten	four	−0.3	2.2	2,500	40%
10 ²	25	3.3	5.1	4,000	25%
10 ³	168	23	ten	5,952	16.8%
10 ⁴	1,229	143	17	8,137	12.3%
10 ⁵	9 592	906	38	10,425	9.59%
10 ⁶	78,498	6 116	130	12,740	7.85%
10 ⁷	664 579	44,158	339	15,047	6.65%
10 ⁸	5 761 455	332,774	754	17,357	5.76%
10 ⁹	50 847 534	2 592 592	1,701	19,667	5.08%
10 ¹⁰	455 052 511	20,758,029	3 104	21,975	4,55%
10 ¹¹	4 118 054 813	169 923 159	11 588	24,283	4.12%
10 ¹²	37 607 912 018	1 416 705 193	38,263	26,590	3.76%
10 ¹³	346 065 536 839	11 992 858 452	108 971	28,896	3.46%
10 ¹⁴	3 204 941 750 802	102 838 308 636	314,890	31,202	3.20%
10 ¹⁵	29 844 570 422 669	891 604 962 452	1,052,619	33,507	2.98%
10 ¹⁶	279 238 341 033 925	7 804 289 844 393	3,214,632	35,812	2.79%
10 ¹⁷	2 623 557 157 654 233	68 883 734 693 281	7 956 589	38,116	2.62%
10 ¹⁸	24 739 954 287 740 860	612 483 070 893 536	21 949 555	40,420	2.47%
10 ¹⁹	234 057 667 276 344 607	5 481 624 169 369 960	99 877 775	42,725	2.34%
10 ²⁰	2 220 819 602 560 918 840	49 347 193 044 659 701	222 744 644	45,028	2.22%
10 ²¹	21 127 269 486 018 731 928	446 579 871 578 168 707	597 394 254	47,332	2.11%
10 ²²	201 467 286 689 315 906 290	4,060,704,006,019,620,994	1 932 355 208	49,636	2.01%
10 ²³	1 925 320 391 606 803 968 923	37 083 513 766 578 631 309	7 250 186 216	51,939	1.92%
10 ²⁴	18 435 599 767 349 200 867 866	339 996 354 713 708 049 069	17 146 907 278	54,243	1.84%
10 ²⁵	176 846 309 399 143 769 411 680	3 128 516 637 843 038 351 228	55 160 980 939	56,546	1.77%
10 ²⁶	1 699 246 750 872 437 141 327 603	28 883 358 936 853 188 823 261	155 891 678 121	58,850	1.70%
10 ²⁷	16 352 460 426 841 680 446 427 399	267 479 615 610 131 274 163 365	508 666 658 006	61,153	1.64%

In OEIS, the first column of values $\pi (x)$ ${\ displaystyle \ pi (x)}$ Is the sequence A006880 , $\pi (x)-\left\lfloor {\frac {x}{\ln x}}+0{,}5\right\rfloor$ ${\ displaystyle \ pi (x) - \ left \ lfloor {\ frac {x} {\ ln x}} + 0 {,} 5 \ right \ rfloor}$ Is the sequence A057835 , and $\lfloor \operatorname {li} (x)+0{,}5\rfloor -\pi (x)$ ${\ displaystyle \ lfloor \ operatorname {li} (x) +0 {,} 5 \ rfloor - \ pi (x)}$ Is the sequence A057752 .

Pi-function calculation algorithms

Easy way to find $\pi (x)$ ${\ displaystyle \ pi (x)}$ , if a $x$ ${\ displaystyle x}$ not very large - this is the use of the sieve of Eratosthenes issuing simple, not superior $x$ ${\ displaystyle x}$ and count them.

A more thoughtful way to calculate $\pi (x)$ ${\ displaystyle \ pi (x)}$ was given by Legendre : given $x$ ${\ displaystyle x}$ , if a $p_{1},p_{2},\ldots ,p_{k}$ ${\ displaystyle p_ {1}, p_ {2}, \ ldots, p_ {k}}$ - various primes, then the number of integers not exceeding $x$ ${\ displaystyle x}$ and not dividing into everything $p_{i}$ ${\ displaystyle p_ {i}}$ equally

\lfloor x\rfloor -\sum _{i}\left\lfloor {\frac {x}{p_{i}}}\right\rfloor +\sum _{i<j}\left\lfloor {\frac {x}{p_{i}p_{j}}}\right\rfloor -\sum _{i<j<k}\left\lfloor {\frac {x}{p_{i}p_{j}p_{k}}}\right\rfloor +\cdots

{\ displaystyle \ lfloor x \ rfloor - \ sum _ {i} \ left \ lfloor {\ frac {x} {p_ {i}}} \ right \ rfloor + \ sum _ {i <j} \ left \ lfloor { \ frac {x} {p_ {i} p_ {j}}} \ right \ rfloor - \ sum _ {i <j <k} \ left \ lfloor {\ frac {x} {p_ {i} p_ {j} p_ {k}}} \ right \ rfloor + \ cdots}

(Where $\lfloor \cdots \rfloor$ ${\ displaystyle \ lfloor \ cdots \ rfloor}$ denotes the integer part ). Therefore, the resulting number is equal to

\pi (x)-\pi \left({\sqrt {x}}\right)+1

{\ displaystyle \ pi (x) - \ pi \ left ({\ sqrt {x}} \ right) +1}

if numbers $p_{1},p_{2},\ldots ,p_{k}$ ${\ displaystyle p_ {1}, p_ {2}, \ ldots, p_ {k}}$ Are all prime numbers not exceeding ${\sqrt {x}}$ ${\ displaystyle {\ sqrt {x}}}$ .

In a series of articles from 1870-1885, Ernst Meissel described (and used) a practical combinatorial method $\pi (x)$ ${\ displaystyle \ pi (x)}$ . Let be $p_{1},p_{2},\ldots ,p_{n}$ ${\ displaystyle p_ {1}, p_ {2}, \ ldots, p_ {n}}$ - first $n$ ${\ displaystyle n}$ simple, we denote $\Phi (m,n)$ ${\ displaystyle \ Phi (m, n)}$ the number of natural numbers not exceeding $m$ ${\ displaystyle m}$ which are not divisible by any $p_{i}$ ${\ displaystyle p_ {i}}$ . Then

\Phi (m,n)=\Phi (m,n-1)-\Phi \left(\left[{\frac {m}{p_{n}}}\right],n-1\right)

{\ displaystyle \ Phi (m, n) = \ Phi (m, n-1) - \ Phi \ left (\ left [{\ frac {m} {p_ {n}}} \ right], n-1 \ right)}

Take natural $m$ ${\ displaystyle m}$ , if a $n=\pi \left({\sqrt[{3}]{m}}\right)$ ${\ displaystyle n = \ pi \ left ({\ sqrt [{3}] {m}} \ right)}$ and if $\mu =\pi \left({\sqrt {m}}\right)-n$ ${\ displaystyle \ mu = \ pi \ left ({\ sqrt {m}} \ right) -n}$ then

\pi (m)=\Phi (m,n)+n(\mu +1)+{\frac {\mu ^{2}-\mu }{2}}-1-\sum _{k=1}^{\mu }\pi \left({\frac {m}{p_{n+k}}}\right)

{\ displaystyle \ pi (m) = \ Phi (m, n) + n (\ mu +1) + {\ frac {\ mu ^ {2} - \ mu} {2}} - 1- \ sum _ { k = 1} ^ {\ mu} \ pi \ left ({\ frac {m} {p_ {n + k}}} \ right)}

Using this approach, Meissel calculated $\pi (x)$ ${\ displaystyle \ pi (x)}$ for $x=5\cdot 10^{5};10^{6};10^{7};10^{8}$ ${\ displaystyle x = 5 \ cdot 10 ^ {5}; 10 ^ {6}; 10 ^ {7}; 10 ^ {8}}$ .

In 1959, Derrick Henry Lemer expanded and simplified the Meissel method. We define for real $m$ ${\ displaystyle m}$ and for natural $n, k$ ${\ displaystyle n, k}$ value $P_{k}(m,n)$ ${\ displaystyle P_ {k} (m, n)}$ as the number of numbers not exceeding m having exactly k prime factors, all of which exceed $p_{n}$ ${\ displaystyle p_ {n}}$ . In addition, we put $P_{0}(m,n)=1$ ${\ displaystyle P_ {0} (m, n) = 1}$ . Then

\Phi (m,n)=\sum _{k=0}^{+\infty }P_{k}(m,n)

{\ displaystyle \ Phi (m, n) = \ sum _ {k = 0} ^ {+ \ infty} P_ {k} (m, n)}

where the sum obviously always has a finite number of nonzero terms. Let be $y$ ${\ displaystyle y}$ - a whole such that ${\sqrt[{3}]{m}}\leqslant y\leqslant {\sqrt {m}}$ ${\ displaystyle {\ sqrt [{3}] {m}} \ leqslant y \ leqslant {\ sqrt {m}}}$ and put $n=\pi (y)$ ${\ displaystyle n = \ pi (y)}$ . Then $P_{1}(m,n)=\pi (m)-n$ ${\ displaystyle P_ {1} (m, n) = \ pi (m) -n}$ and $P_{k}(m,n)=0$ ${\ displaystyle P_ {k} (m, n) = 0}$ at $k\geqslant 3$ ${\ displaystyle k \ geqslant 3}$ . Consequently

\pi (m)=\Phi (m,n)+n-1-P_{2}(m,n)

{\ displaystyle \ pi (m) = \ Phi (m, n) + n-1-P_ {2} (m, n)}

Calculation $P_{2}(m,n)$ ${\ displaystyle P_ {2} (m, n)}$ can be obtained in the following way:

{\displaystyle P_{2}(m,n)=\sum _{y<semantics><mrow class=

{\ displaystyle P_ {2} (m, n) = \ sum _ {y <p \ leqslant {\ sqrt {m}}} \ left (\ pi \ left ({\ frac {m} {p}} \ right ) - \ pi (p) +1 \ right)}

On the other hand, computing $\Phi (m,n)$ ${\ displaystyle \ Phi (m, n)}$ can be performed using the following rules:

$\Phi (m,0)=\lfloor m\rfloor$ ${\ displaystyle \ Phi (m, 0) = \ lfloor m \ rfloor}$
$\Phi (m,b)=\Phi (m,b-1)-\Phi \left({\frac {m}{p_{b}}},b-1\right)$ ${\ displaystyle \ Phi (m, b) = \ Phi (m, b-1) - \ Phi \ left ({\ frac {m} {p_ {b}}}, b-1 \ right)}$

Using this method and IBM 701, Lehmer was able to calculate $\pi \left(10^{10}\right)$ ${\ displaystyle \ pi \ left (10 ^ {10} \ right)}$ .

Further improvements to this method were made by Lagarias, Miller, Odlyzko, Deleglise, and Rivat. ^[9]

The Chinese mathematician Hwang Cheng used the following identities: ^[10]

e^{(a-1)\Theta }f(x)=f(ax),

{\ displaystyle e ^ {(a-1) \ Theta} f (x) = f (ax),}

J(x)=\sum _{n=1}^{\infty }{\frac {\pi (x^{1/n})}{n}}

{\ displaystyle J (x) = \ sum _ {n = 1} ^ {\ infty} {\ frac {\ pi (x ^ {1 / n})} {n}}}

and assuming $x=e^{t}$ ${\ displaystyle x = e ^ {t}}$ performing the Laplace transform of both parts and applying the sum of the geometric progression with $e^{n\Theta }$ ${\ displaystyle e ^ {n \ Theta}}$ received the expression:

{\frac {1}{2{\pi }i}}\int _{c-i\infty }^{c+i\infty }g(s)t^{s}\,ds=\pi (t)

{\ displaystyle {\ frac {1} {2 {\ pi} i}} \ int _ {ci \ infty} ^ {c + i \ infty} g (s) t ^ {s} \, ds = \ pi ( t)}

{\frac {\ln \zeta (s)}{s}}=(1-e^{\Theta (s)})^{-1}g(s)

{\ displaystyle {\ frac {\ ln \ zeta (s)} {s}} = (1-e ^ {\ Theta (s)}) ^ {- 1} g (s)}

\Theta (s)=s{\frac {d}{ds}}

{\ displaystyle \ Theta (s) = s {\ frac {d} {ds}}}

Other functions that count prime numbers

Other functions that count primes are also used, since they are more convenient to work with. One of them is the Riemann function, often denoted as $\Pi _{0}(x)$ ${\ displaystyle \ Pi _ {0} (x)}$ or $J_{0}(x)$ ${\ displaystyle J_ {0} (x)}$ . She has a 1 / n jump for simple degrees $p^{n}$ ${\ displaystyle p ^ {n}}$ , and at the jump point $x$ ${\ displaystyle x}$ its value is equal to half the sum of the values on both sides of $x$ ${\ displaystyle x}$ . These additional details are needed so that it can be determined by the inverse Mellin transform . Formally, we will define $\Pi _{0}(x)$ ${\ displaystyle \ Pi _ {0} (x)}$ as

\Pi _{0}(x)={\frac {1}{2}}{\bigg (}\sum _{p^{n}<x}{\frac {1}{n}}\ +\sum _{p^{n}\leq x}{\frac {1}{n}}{\bigg )}

{\ displaystyle \ Pi _ {0} (x) = {\ frac {1} {2}} {\ bigg (} \ sum _ {p ^ {n} <x} {\ frac {1} {n}} \ + \ sum _ {p ^ {n} \ leq x} {\ frac {1} {n}} {\ bigg)}}

where p is prime.

We can also record

\Pi _{0}(x)=\sum \limits _{n=2}^{x}{\frac {\Lambda (n)}{\ln n}}-{\frac {1}{2}}{\frac {\Lambda (x)}{\ln x}}=\sum _{n=1}^{\infty }{\frac {1}{n}}\pi _{0}({\sqrt[{n}]{x}})

{\ displaystyle \ Pi _ {0} (x) = \ sum \ limits _ {n = 2} ^ {x} {\ frac {\ Lambda (n)} {\ ln n}} - {\ frac {1} {2}} {\ frac {\ Lambda (x)} {\ ln x}} = \ sum _ {n = 1} ^ {\ infty} {\ frac {1} {n}} \ pi _ {0} ({\ sqrt [{n}] {x}})}

Where $\Lambda (n)$ ${\ displaystyle \ Lambda (n)}$ - Mangoldt function and

\pi _{0}(x)=\lim _{\varepsilon \rightarrow 0}{\frac {\pi (x-\varepsilon )+\pi (x+\varepsilon )}{2}}.

{\ displaystyle \ pi _ {0} (x) = \ lim _ {\ varepsilon \ rightarrow 0} {\ frac {\ pi (x- \ varepsilon) + \ pi (x + \ varepsilon)} {2}}.}

Mobius formula gives

\pi _{0}(x)=\sum _{n=1}^{\infty }{\frac {\mu (n)}{n}}\Pi _{0}({\sqrt[{n}]{x}})

{\ displaystyle \ pi _ {0} (x) = \ sum _ {n = 1} ^ {\ infty} {\ frac {\ mu (n)} {n}} \ Pi _ {0} ({\ sqrt [{n}] {x}})}

Using the well-known relation between the logarithm of the Riemann zeta function and the Mangoldt function $\Lambda$ ${\ displaystyle \ Lambda}$ , and using the Perron formula we get

\ln \zeta (s)=s\int _{0}^{\infty }\Pi _{0}(x)x^{-s-1}\,dx

{\ displaystyle \ ln \ zeta (s) = s \ int _ {0} ^ {\ infty} \ Pi _ {0} (x) x ^ {- s-1} \, dx}

Riemann function has a generating function

\sum _{n=1}^{\infty }\Pi _{0}(n)x^{n}=\sum _{a=2}^{\infty }{\frac {x^{a}}{1-x}}-{\frac {1}{2}}\sum _{a=2}^{\infty }\sum _{b=2}^{\infty }{\frac {x^{ab}}{1-x}}+{\frac {1}{3}}\sum _{a=2}^{\infty }\sum _{b=2}^{\infty }\sum _{c=2}^{\infty }{\frac {x^{abc}}{1-x}}-{\frac {1}{4}}\sum _{a=2}^{\infty }\sum _{b=2}^{\infty }\sum _{c=2}^{\infty }\sum _{d=2}^{\infty }{\frac {x^{abcd}}{1-x}}+\cdots

{\ displaystyle \ sum _ {n = 1} ^ {\ infty} \ Pi _ {0} (n) x ^ {n} = \ sum _ {a = 2} ^ {\ infty} {\ frac {x ^ {a}} {1-x}} - {\ frac {1} {2}} \ sum _ {a = 2} ^ {\ infty} \ sum _ {b = 2} ^ {\ infty} {\ frac {x ^ {ab}} {1-x}} + {\ frac {1} {3}} \ sum _ {a = 2} ^ {\ infty} \ sum _ {b = 2} ^ {\ infty} \ sum _ {c = 2} ^ {\ infty} {\ frac {x ^ {abc}} {1-x}} - {\ frac {1} {4}} \ sum _ {a = 2} ^ { \ infty} \ sum _ {b = 2} ^ {\ infty} \ sum _ {c = 2} ^ {\ infty} \ sum _ {d = 2} ^ {\ infty} {\ frac {x ^ {abcd }} {1-x}} + \ cdots}

Chebyshev functions are functions that calculate the powers of primes $p^{n}$ ${\ displaystyle p ^ {n}}$ with weight $\ln p$ ${\ displaystyle \ ln p}$ :

\theta (x)=\sum _{p\leqslant x}\ln p

{\ displaystyle \ theta (x) = \ sum _ {p \ leqslant x} \ ln p}

\psi (x)=\sum _{p^{n}\leqslant x}\ln p=\sum _{n=1}^{\infty }\theta ({\sqrt[{n}]{x}})=\sum _{n\leqslant x}\Lambda (n).

{\ displaystyle \ psi (x) = \ sum _ {p ^ {n} \ leqslant x} \ ln p = \ sum _ {n = 1} ^ {\ infty} \ theta ({\ sqrt [{n}] {x}}) = \ sum _ {n \ leqslant x} \ Lambda (n).}

Formulas for functions that count prime numbers

Formulas for functions that count prime numbers come in two forms: arithmetic formulas and analytical formulas. Analytical formulas for such functions were first used to prove the prime number theorem . They come from the work of Riemann and Mangoldt and are generally known as explicit formulas . ^[eleven]

The following expression exists for $\psi$ ${\ displaystyle \ psi}$ Chebyshev functions:

\psi _{0}(x)=x-\sum _{\rho }{\frac {x^{\rho }}{\rho }}-\ln 2\pi -{\frac {1}{2}}\ln(1-x^{-2})

{\ displaystyle \ psi _ {0} (x) = x- \ sum _ {\ rho} {\ frac {x ^ {\ rho}} {\ rho}} - \ ln 2 \ pi - {\ frac {1 } {2}} \ ln (1-x ^ {- 2})}

Where

\psi _{0}(x)=\lim _{\varepsilon \rightarrow 0}{\frac {\psi (x-\varepsilon )+\psi (x+\varepsilon )}{2}}.

{\ displaystyle \ psi _ {0} (x) = \ lim _ {\ varepsilon \ rightarrow 0} {\ frac {\ psi (x- \ varepsilon) + \ psi (x + \ varepsilon)} {2}}.}

Here $\rho$ ${\ displaystyle \ rho}$ runs through zeros of the zeta function in the critical strip, where the real part $\rho$ ${\ displaystyle \ rho}$ lies between zero and one. The formula is true for everyone $x>1$ ${\ displaystyle x> 1}$ . A series of roots converges conditionally, and can be taken in order of the absolute value of the increase in the imaginary part of the roots. Note that a similar sum over trivial roots gives the last term in the formula.

For $\scriptstyle \Pi _{0}(x)$ ${\ displaystyle \ scriptstyle \ Pi _ {0} (x)}$ we have the following complex formula

\Pi _{0}(x)=\operatorname {li} (x)-\sum _{\rho }\operatorname {li} (x^{\rho })-\ln 2+\int _{x}^{\infty }{\frac {dt}{t(t^{2}-1)\ln t}}.

{\ displaystyle \ Pi _ {0} (x) = \ operatorname {li} (x) - \ sum _ {\ rho} \ operatorname {li} (x ^ {\ rho}) - \ ln 2+ \ int _ {x} ^ {\ infty} {\ frac {dt} {t (t ^ {2} -1) \ ln t}}.}

Again, the formula is true for everyone $x>1$ ${\ displaystyle x> 1}$ where $\rho$ ${\ displaystyle \ rho}$ - non-trivial zeros of the zeta function, ordered by their absolute value, and, again, the last integral is taken with a minus sign and is the same sum, but with trivial zeros. Expression $\operatorname {li} (x^{\rho })$ ${\ displaystyle \ operatorname {li} (x ^ {\ rho})}$ in the second term can be considered as $\operatorname {Ei} (\rho \ln x)$ ${\ displaystyle \ operatorname {Ei} (\ rho \ ln x)}$ where $\operatorname {Ei}$ ${\ displaystyle \ operatorname {Ei}}$ Is an analytic continuation of the integral exponential function onto a complex plane with a branch cut along a straight line $x<0$ ${\ displaystyle x <0}$ .

Thus, the Mobius inversion formula gives us ^[12]

\pi _{0}(x)=\operatorname {R} (x)-\sum _{\rho }\operatorname {R} (x^{\rho })-{\frac {1}{\ln x}}+{\frac {1}{\pi }}\mathop {\mathrm {arctg} } {\frac {\pi }{\ln x}}

{\ displaystyle \ pi _ {0} (x) = \ operatorname {R} (x) - \ sum _ {\ rho} \ operatorname {R} (x ^ {\ rho}) - {\ frac {1} { \ ln x}} + {\ frac {1} {\ pi}} \ mathop {\ mathrm {arctg}} {\ frac {\ pi} {\ ln x}}}

true for $x>1$ ${\ displaystyle x> 1}$ where

\operatorname {R} (x)=\sum _{n=1}^{\infty }{\frac {\mu (n)}{n}}\operatorname {li} (x^{1/n})=1+\sum _{k=1}^{\infty }{\frac {(\ln x)^{k}}{k!k\zeta (k+1)}}

{\ displaystyle \ operatorname {R} (x) = \ sum _ {n = 1} ^ {\ infty} {\ frac {\ mu (n)} {n}} \ operatorname {li} (x ^ {1 / n}) = 1+ \ sum _ {k = 1} ^ {\ infty} {\ frac {(\ ln x) ^ {k}} {k! k \ zeta (k + 1)}}}

called the R-function also after Riemann. ^[13] The last row in it is known as the Gram series ^[14] and converges for all $x>0$ ${\ displaystyle x> 0}$ .

The sum over the nontrivial zeros of the zeta function in the formula for $\pi _{0}(x)$ ${\ displaystyle \ pi _ {0} (x)}$ describes fluctuations $\pi _{0}(x)$ ${\ displaystyle \ pi _ {0} (x)}$ , while the remaining terms give the smooth part of the pi-function, ^[15] so we can use

\operatorname {R} (x)-{\frac {1}{\ln x}}+{\frac {1}{\pi }}\mathop {\mathrm {arctg} } {\frac {\pi }{\ln x}}

{\ displaystyle \ operatorname {R} (x) - {\ frac {1} {\ ln x}} + {\ frac {1} {\ pi}} \ mathop {\ mathrm {arctg}} {\ frac {\ pi} {\ ln x}}}

as the best approximation for $\pi (x)$ ${\ displaystyle \ pi (x)}$ for $x>1$ ${\ displaystyle x> 1}$ .

The amplitude of the “noisy” part is heuristically estimated as ${\sqrt {x}}/\ln x$ ${\ displaystyle {\ sqrt {x}} / \ ln x}$ , therefore, fluctuations in the distribution of primes can be explicitly represented $\Delta$ ${\ displaystyle \ Delta}$ -function:

\Delta (x)=\left(\pi _{0}(x)-\operatorname {R} (x)+{\frac {1}{\ln x}}-{\frac {1}{\pi }}\mathop {\mathrm {arctg} } {\frac {\pi }{\ln x}}\right){\frac {\ln x}{\sqrt {x}}}.

{\ displaystyle \ Delta (x) = \ left (\ pi _ {0} (x) - \ operatorname {R} (x) + {\ frac {1} {\ ln x}} - {\ frac {1} {\ pi}} \ mathop {\ mathrm {arctg}} {\ frac {\ pi} {\ ln x}} \ right) {\ frac {\ ln x} {\ sqrt {x}}}.}

Extensive value tables $\Delta (x)$ ${\ displaystyle \ Delta (x)}$ available here. ^[7]

Inequalities

Some inequalities for $\pi (x)$ ${\ displaystyle \ pi (x)}$ .

{\frac {x}{\ln x}}<\pi (x)<1{,}25506\cdot {\frac {x}{\ln x}}\qquad x\geqslant 17.

{\ displaystyle {\ frac {x} {\ ln x}} <\ pi (x) <1 {,} 25506 \ cdot {\ frac {x} {\ ln x}} \ qquad x \ geqslant 17.}

The left inequality holds for $x\geqslant 17$ ${\ displaystyle x \ geqslant 17}$ , and the right - with $x>1.$ ${\ displaystyle x> 1.}$ ^[sixteen]

Inequalities for $n$ ${\ displaystyle n}$ prime number $p_{n}$ ${\ displaystyle p_ {n}}$ :

n\ln n+n\ln \ln n-n<p_{n}<n\ln n+n\ln \ln n,\ n\geqslant 6

{\ displaystyle n \ ln n + n \ ln \ ln nn <p_ {n} <n \ ln n + n \ ln \ ln n, \ n \ geqslant 6}

The left inequality is true for $n\geqslant 1$ ${\ displaystyle n \ geqslant 1}$ , and the right - with $n\geqslant 6$ ${\ displaystyle n \ geqslant 6}$ .

The following asymptotics holds for $n$ ${\ displaystyle n}$ prime number $p_{n}$ ${\ displaystyle p_ {n}}$ :

p_{n}=n\ln n\left(1+{\frac {\ln \ln n-1}{\ln n}}+{\frac {\ln \ln n-2}{\ln ^{2}n}}+{\frac {-1/2\ln ^{2}\ln n+3\ln \ln n-11/2}{\ln ^{3}n}}+O\left({\frac {\ln ^{3}\ln n}{\ln ^{4}n}}\right)\right)

{\ displaystyle p_ {n} = n \ ln n \ left (1 + {\ frac {\ ln \ ln n-1} {\ ln n}} + {\ frac {\ ln \ ln n-2} {\ ln ^ {2} n}} + {\ frac {-1/2 \ ln ^ {2} \ ln n + 3 \ ln \ ln n-11/2} {\ ln ^ {3} n}} + O \ left ({\ frac {\ ln ^ {3} \ ln n} {\ ln ^ {4} n}} \ right) \ right)}

Riemann hypothesis

The Riemann hypothesis is equivalent to a more accurate boundary of the approximation error $\pi (x)$ ${\ displaystyle \ pi (x)}$ integral logarithm, and hence the more regular distribution of primes

\pi (x)=\operatorname {li} (x)+O({\sqrt {x}}\ln x).

{\ displaystyle \ pi (x) = \ operatorname {li} (x) + O ({\ sqrt {x}} \ ln x).}

In particular, ^[17]

|\pi (x)-\operatorname {li} (x)|<{\frac {1}{8\pi }}{\sqrt {x}}\,\ln x,\qquad x\geqslant 2657.

{\ displaystyle | \ pi (x) - \ operatorname {li} (x) | <{\ frac {1} {8 \ pi}} {\ sqrt {x}} \, \ ln x, \ qquad x \ geqslant 2657.}

Notes

↑ Bach, Eric. Section 8.8 // Algorithmic Number Theory. - MIT Press, 1996. - Vol. 1. - P. 234. - ISBN 0-262-02405-5 .
↑ Weisstein, Eric W. Prime Counting Function on the Wolfram MathWorld website.
↑ ¹ ² How many primes are there? (unspecified) . Chris K. Caldwell. Date of treatment December 2, 2008. Archived on September 20, 2012.
↑ Dickson, Leonard Eugene. History of the Theory of Numbers I: Divisibility and Primality. - Dover Publications, 2005. - ISBN 0-486-44232-2 .
↑ K. Ireland, M. Rosen. A Classical Introduction to Modern Number Theory. - Second. - Springer, 1998 .-- ISBN 0-387-97329-X .
↑ Tables of values of pi (x) and of pi2 (x) (unspecified) . Tomas Oliveira e Silva . Date of treatment September 14, 2008. Archived on September 20, 2012.
↑ ¹ ² Values of π (x) and Δ (x) for various x's (neopr.) . Andrey V. Kulsha. Date of treatment September 14, 2008. Archived on September 20, 2012.
↑ A table of values of pi (x) (unspecified) . Xavier Gourdon, Pascal Sebah, Patrick Demichel. Date of treatment September 14, 2008. Archived on September 20, 2012.
↑ Computing? (X): The Meissel, Lehmer, Lagarias, Miller, Odlyzko method (neopr.) . Marc Deleglise and Joel Rivat, Mathematics of Computation , vol. 65 , number 33, January 1996, pages 235-245. Date of treatment September 14, 2008. Archived on September 20, 2012.
↑ Hwang H., Cheng . Demarches de la Geometrie et des Nombres de l'Universite du Bordeaux, Prime Magic conference.
↑ Titchmarsh, EC The Theory of Functions, 2nd ed .. - Oxford University Press, 1960.
↑ Riesel, Hans ; Gohl, Gunnar. Some calculations related to Riemann's prime number formula (English) // Mathematics of Computation : journal. - American Mathematical Society, 1970. - Vol. 24 , no. 112 . - P. 969–983 . - ISSN 0025-5718 . - DOI : 10.2307 / 2004630 .
↑ Weisstein, Eric W. Riemann Prime Counting Function ( Wolfram MathWorld) .
↑ Weisstein, Eric W. Gram Series on the Wolfram MathWorld website.
↑ The encoding of the prime distribution by the zeta zeros (neopr.) . Matthew Watkins. Date of treatment September 14, 2008. Archived on September 20, 2012.
↑ Rosser, J. Barkley ; Schoenfeld, Lowell. Approximate formulas for some functions of prime numbers (Ill.) // Illinois J. Math. : journal. - 1962. - Vol. 6 . - P. 64-94 . - ISSN 0019-2082 .
↑ Lowell Schoenfeld. Sharper bounds for the Chebyshev functions θ ( x ) and ψ ( x ). II (Eng.) // Mathematics of Computation : journal. - American Mathematical Society, 1976. - Vol. 30 , no. 134 . - P. 337-360 . - ISSN 0025-5718 . - DOI : 10.2307 / 2005976 .

Literature

C. Prahar. The distribution of primes. - World, 1967.
V.I. Zenkin. The distribution of primes. Elementary methods. Kaliningrad, 2008.

Links

Chris Caldwell, The Nth Prime Page at The Prime Pages .

[Bach-1] Bach, Eric. Section 8.8 // Algorithmic Number Theory. - MIT Press, 1996. - Vol. 1. - P. 234. - ISBN 0-262-02405-5 .

[mathworld_pcf-2] Weisstein, Eric W. Prime Counting Function on the Wolfram MathWorld website.

[Caldwell-3] ¹ ² How many primes are there? (unspecified) . Chris K. Caldwell. Date of treatment December 2, 2008. Archived on September 20, 2012.

[Dickson-4] Dickson, Leonard Eugene. History of the Theory of Numbers I: Divisibility and Primality. - Dover Publications, 2005. - ISBN 0-486-44232-2 .

[Ireland-5] K. Ireland, M. Rosen. A Classical Introduction to Modern Number Theory. - Second. - Springer, 1998 .-- ISBN 0-387-97329-X .

[Silva-6] Tables of values of pi (x) and of pi2 (x) (unspecified) . Tomas Oliveira e Silva . Date of treatment September 14, 2008. Archived on September 20, 2012.

[Kulsha-7] ¹ ² Values of π (x) and Δ (x) for various x's (neopr.) . Andrey V. Kulsha. Date of treatment September 14, 2008. Archived on September 20, 2012.

[Gourdon-8] A table of values of pi (x) (unspecified) . Xavier Gourdon, Pascal Sebah, Patrick Demichel. Date of treatment September 14, 2008. Archived on September 20, 2012.

[pix_comp-9] Computing? (X): The Meissel, Lehmer, Lagarias, Miller, Odlyzko method (neopr.) . Marc Deleglise and Joel Rivat, Mathematics of Computation , vol. 65 , number 33, January 1996, pages 235-245. Date of treatment September 14, 2008. Archived on September 20, 2012.

[Cheng-10] Hwang H., Cheng . Demarches de la Geometrie et des Nombres de l'Universite du Bordeaux, Prime Magic conference.

[Titchmarsh-11] Titchmarsh, EC The Theory of Functions, 2nd ed .. - Oxford University Press, 1960.

[12] Riesel, Hans ; Gohl, Gunnar. Some calculations related to Riemann's prime number formula (English) // Mathematics of Computation : journal. - American Mathematical Society, 1970. - Vol. 24 , no. 112 . - P. 969–983 . - ISSN 0025-5718 . - DOI : 10.2307 / 2004630 .

[mathworld_r-13] Weisstein, Eric W. Riemann Prime Counting Function ( Wolfram MathWorld) .

[mathworld_gram-14] Weisstein, Eric W. Gram Series on the Wolfram MathWorld website.

[Watkins-15] The encoding of the prime distribution by the zeta zeros (neopr.) . Matthew Watkins. Date of treatment September 14, 2008. Archived on September 20, 2012.

[16] Rosser, J. Barkley ; Schoenfeld, Lowell. Approximate formulas for some functions of prime numbers (Ill.) // Illinois J. Math. : journal. - 1962. - Vol. 6 . - P. 64-94 . - ISSN 0019-2082 .

[17] Lowell Schoenfeld. Sharper bounds for the Chebyshev functions θ ( x ) and ψ ( x ). II (Eng.) // Mathematics of Computation : journal. - American Mathematical Society, 1976. - Vol. 30 , no. 134 . - P. 337-360 . - ISSN 0025-5718 . - DOI : 10.2307 / 2005976 .