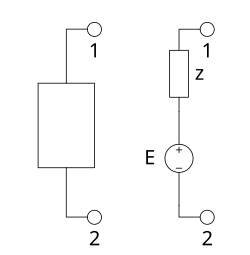
The internal resistance of a two - terminal device is the impedance in the equivalent circuit of a two-terminal device, consisting of a voltage and impedance generator connected in series (see figure). The concept is used in circuit theory when replacing a real source with ideal elements, that is, when moving to an equivalent circuit.
Content
Introduction
The need to introduce the term can be illustrated by the following example. Compare two chemical DC sources with the same voltage:
- Car lead-acid battery with a voltage of 12 volts and a capacity of 55 Ah .
- Battery of 8 galvanic cells , for example, size AA, connected in series. The total voltage of such a battery is also 12 volts, the capacity is much less - about 1 Ah.
Despite the same voltage, these sources differ significantly when working at the same load. So, a car battery is capable of delivering a large current to the load (the car engine starts up from the battery, while the starter consumes a current of about 250 A ), and the starter does not rotate from the battery of elements, since the voltage of the battery when connected to the starter terminals drops to a fraction of a volt . It's not about the relatively small electrical capacity of the batteries: the energy stored in it and a charge of one ampere hour would be enough to rotate the starter for 14 seconds (at a current of 250 A).
In accordance with Ohm's law, in sources with the same voltage, the current in the same load must also be the same. In the given example, this is not fulfilled because the statement is true only for ideal sources of EMF ; real sources, to one degree or another, differ from ideal sources. To describe the degree of difference between real sources and ideal sources, the concept of internal resistance is used .
Equivalent active two-terminal circuit
Real active two-terminal circuits are well described mathematically, if they are considered as an equivalent circuit consisting of a voltage and resistance generator (in general, an impedance ) connected in series (see figure). The voltage generator is actually the energy source located in this two-terminal network. An ideal generator could give an arbitrarily large power and current to the load. However, the resistance connected in series with the generator limits the power that this two-terminal can give to the load. This equivalent resistance is called internal resistance . It is only a parameter of the abstract two-terminal model, that is, there is usually no physical “resistor” as an electronic component inside two-terminal devices.
Formally, in real galvanic cells, this internal resistance can be identified physically. This is the total resistance of the positive rod (carbon, steel), the body itself (zinc and nickel), as well as the electrolyte (salt) and the hydrogen absorber (in salt elements). All these materials, as well as the interface between them, have a finite resistance other than zero.
In other sources, this ohmic resistance is due to the resistance of the windings and contacts, which is connected in series with the internal resistance of the source itself and reduce the characteristics of voltage sources.
Contact potential differences have a different nature of the occurrence of voltage and are non-ohmic, that is, here the energy costs go to the work function of the charge carriers.
Resistance and internal resistance
The main characteristic of an abstract bipolar is its internal resistance (or, otherwise, impedance [1] ). However, it is not always possible to describe a bipolar by resistance alone. The fact is that the term resistance is applicable only to purely passive elements, that is, not containing energy sources. If the two-terminal network contains an energy source, then the concept of “resistance” is simply not applicable to it, since Ohm’s law in the formulation U = I · r does not hold [2] .
Thus, for dvukhpolosnykh containing sources (that is , voltage generators and current generators ) it is necessary to talk about the internal resistance (or impedance). If the two-terminal network does not contain sources [3] , then “ internal resistance” for such a two-terminal network means the same as simply “resistance”.
Related Terms
If an input and / or output (a pair of electrical contacts) can be distinguished in any system, the following terms are often used:
- Input resistance , often input impedance , is the internal resistance exhibited by this pair of contacts as a two-terminal device, which is the input of the system [4]
- The output impedance , often the output impedance , is the internal resistance exhibited by this pair of contacts as a two-terminal device, which is the system output .
Physical Principles
Despite the fact that in the equivalent circuit the internal resistance is presented as one passive element (moreover, the active resistance , that is, the resistor is necessarily present in it), the internal resistance is not necessarily concentrated in any one element. The bipolar only behaves externally as if it has a concentrated internal impedance and a voltage generator. In reality, internal resistance is an external manifestation of a combination of physical effects:
- If in a two-terminal network there is only an energy source without any electrical circuit (for example, a galvanic cell ), then the internal resistance is purely active (in low-frequency circuits), and it is due to physical effects that do not allow the power given by this source to the load, exceed a certain limit. The simplest example of such an effect is the non-zero resistance of the conductors of an electrical circuit. But, as a rule, effects of non-electric nature make the greatest contribution to power limitation. So, for example, in a chemical source, the power can be limited by the contact area of the substances involved in the reaction, in the generator of a hydroelectric power station - by the limited pressure of water, etc.
- In the case of a two-terminal network containing an internal electrical circuit , the internal resistance is "dispersed" in the circuit elements (in addition to the above mechanisms in the source).
From here also follow some features of internal resistance:
- Internal resistance cannot be removed from a two-terminal network [5]
- The internal resistance is not a stable value: it can change when any external (load, current) and internal (heating, depletion of reagents) conditions change.
Effect of internal resistance on the properties of a two-terminal network
The effect of internal resistance is an integral property of any active two-terminal device. The main result of the presence of internal resistance is the limitation of the electric power that can be obtained in the load supplied by this two-terminal device.
If a load with a resistance R is connected to a source with an EMF [6] of the voltage generator E and active internal resistance r , then the current, voltage, and power in the load are expressed as follows:
Finding Inner Resistance
Settlement
The concept of calculation is applicable to the circuit (but not to the real device). The calculation is given for the case of purely active internal resistance (differences in reactance will be discussed later).
Note : Strictly speaking, any real impedance (including internal resistance) has some reactive component, since any conductor has a parasitic inductance and capacitance. When we talk about purely active resistance, we do not mean a real system, but its equivalent circuit , containing only resistors : the reactivity was discarded as insignificant when switching from a real device to its equivalent circuit. If reactivity is significant when considering a real device (for example, when considering a system at high frequencies), then an equivalent circuit is made taking into account this reactivity. See the Equivalent Scheme article for more details.
Suppose there is a two-terminal device that can be described by the equivalent circuit given above. The bipolar has two unknown parameters that must be found:
- EMF voltage generator U
- Internal resistance r
In the general case, to determine two unknowns, it is necessary to make two measurements: measure the voltage at the output of a two-terminal network (i.e., the potential difference U out = φ 2 - φ 1 ) at two different load currents. Then unknown parameters can be found from the system of equations:
| (Stress) |
where U out1 is the output voltage at current I 1 , U out2 is the output voltage at current I 2 . Solving the system of equations, we find the unknown unknowns:
| (General) |
Usually, a simpler method is used to calculate the internal resistance: the voltage is in the no-load mode and the current is in the short-circuit mode of the two-terminal network. In this case, the system ( Voltage ) is written as follows:
where U oc is the output voltage in idle mode ( English open circuit ), that is, at zero load current; I sc - load current in short circuit mode ( eng. Short circuit ), that is, with a load with zero resistance. It is taken into account that the output current in idle mode and the output voltage in short circuit mode are zero. From the last equations we immediately get:
| (IntrSopr) |
Thus, in order to calculate the internal resistance and EMF of an equivalent generator for a two-terminal device, the electrical circuit of which is known, it is necessary:
- Calculate the output voltage of a two-terminal in idle mode
- Calculate the output current of a two-terminal in short circuit mode
- Based on the obtained values, find r and U by the formula ( IntrSopr ).
Measurement
The concept of measurement applies to a real device (but not to a circuit). Direct measurement with an ohmmeter is impossible, since it is impossible to connect the probes of the device to the terminals of internal resistance. Therefore, an indirect measurement is necessary, which does not fundamentally differ from the calculation - voltage on the load is also necessary at two different current values. However, it is not always possible to use the simplified formula (2), since not every real two-terminal network allows operation in the short circuit mode.
Sometimes the following simple measurement method that does not require calculations is applied:
- The open circuit voltage is measured.
- As a load, a variable resistor is connected and its resistance is selected so that the voltage on it is half of the open circuit voltage.
After the described procedures, the resistance of the load resistor must be measured with an ohmmeter - it will be equal to the internal resistance of the two-terminal device.
Whatever measurement method is used, one should beware of overloading the two-terminal network with excessive current, that is, the current should not exceed the maximum permissible values for this two-terminal device.
Reactive Internal Resistance
If the equivalent two-terminal circuit contains reactive elements - capacitors and / or inductors , then the calculation of reactive internal resistance is performed as well as active, but instead of resistors, complex impedances of the elements included in the circuit are taken, and instead of voltages and currents, their complex amplitudes , that is, the calculation is performed by the method of complex amplitudes .
The measurement of reactive internal resistance has some peculiarities, since it is a complex-valued function , and not a scalar value:
- You can search for various parameters of a complex value: a module , an argument , only the real or imaginary part, as well as the complex number in its entirety. Accordingly, the measurement technique will depend on what we want to get.
- Any of these parameters depends on the frequency. Theoretically, in order to obtain complete information about the reactive internal resistance by measuring, it is necessary to remove the dependence on the frequency, that is, take measurements at all frequencies that can be generated by the source of this two-terminal device.
Phase-zero loop resistance measurement
A special case of measuring the internal resistance is the measurement of the resistance of the phase-zero loop in electrical installations. The two-terminal network in this case is a pair of electrical conductors: phase and working neutral conductors or two phase conductors. The photo shows the result of such a measurement in a 220-volt household electrical outlet:
- active component: 0.49 ohm
- reactive component: 0.09 ohm
- impedance module: 0.5 ohm
- expected short circuit current: 440 A
The device finds the internal resistance by indirect measurement by the method of voltage drop across the load resistance. This method is recommended for use in Appendix D of GOST R 50571.16-99. The method is described by the above formula ( GeneralCase ) for I 1 = 0 .
The measurement result is considered satisfactory if the expected short circuit current is large enough for reliable operation of the device that protects this circuit from overcurrent.
Application
In most cases, we should not talk about the use of internal resistance, but about taking into account its negative impact, since internal resistance is more likely a negative effect. However, in some systems, the presence of an internal resistance with a nominal value is simply necessary.
Simplification of equivalent circuits
Representation of a two-terminal network as a combination of a voltage generator and internal resistance is the simplest and often used equivalent circuit of a two-terminal device.
Source and load matching
Matching the source and load is the choice of the ratio of the load resistance and the internal resistance of the source in order to achieve the specified properties of the resulting system (as a rule, they try to achieve the maximum value of any parameter for this source). The most commonly used types of matching are:
- Voltage matching - getting the maximum voltage in a load. For this, the load resistance should be as large as possible , at least much greater than the internal resistance of the source. In other words, the bipolar should be in idle mode. In this case, the maximum voltage attainable in the load is equal to the EMF of the voltage generator E. This type of matching is used in electronic systems when the signal carrier is voltage, and it must be transferred from the source to the load with minimal loss.
- Current matching - getting the maximum current in the load. Для этого сопротивление нагрузки должно быть как можно меньшим , по крайней мере, много меньше , чем внутреннее сопротивление источника. Другими словами, двухполюсник должен быть в режиме короткого замыкания. При этом максимально достижимый в нагрузке ток равен I max =E/r . Применяется в электронных системах, когда носителем сигнала является ток. Например, при съеме сигнала с быстродействующего фотодиода целесообразно применять преобразователь ток-напряжение с минимальным входным сопротивлением. Малое входное сопротивление также решает проблему заужения полосы из-за паразитного RC - фильтра .
- Согласование по мощности — обеспечивает получение в нагрузке (что эквивалентно отбору от источника) максимально возможной мощности, равной P max =E²/(4r) [7] . В цепях постоянного тока: сопротивление нагрузки должно быть равно внутреннему сопротивлению r источника. В цепях переменного тока (в общем случае): импеданс нагрузки должен быть комплексно сопряженным внутреннему импедансу источника.
- Согласование по волновому сопротивлению — получение максимального коэффициента бегущей волны в линии передачи (в СВЧ технике и теории длинных линий ). То же самое, что и согласование по мощности , но применительно к длинным линиям. Волновое сопротивление нагрузки должно быть равно внутреннему сопротивлению r . В СВЧ технике применяется практически всегда. Чаще всего термин согласованная нагрузка используется именно в этом смысле.
Согласование по току и мощности следует использовать с осторожностью, так как есть опасность перегрузить источник.
Понижение высоких напряжений
Иногда к источнику электропитания искусственно добавляют внешнее балластное сопротивление , соединённое последовательно с нагрузкой (оно суммируется с внутренним сопротивлением источника) для того, чтобы понизить получаемое от него напряжение, либо ограничить величину тока, отдаваемого в нагрузку. Однако добавление резистора в качестве дополнительного сопротивления (так называемый гасящий резистор ) во многих случаях неприемлемо, так как ведёт к бесполезному выделению значительной мощности на нём [8] . Чтобы не расходовать энергию впустую и не решать проблему охлаждения дополнительного сопротивления, в системах переменного тока используют реактивные гасящие импедансы. На основе гасящего конденсатора может быть построен конденсаторный блок питания . Аналогично, при помощи ёмкостного отвода от высоковольтной ЛЭП можно получить небольшие напряжения для питания каких-либо автономных устройств. Индуктивный балласт широко применяется для ограничения тока в цепи газоразрядных люминесцентных ламп.
Минимизация шума
При усилении слабых сигналов часто возникает задача минимизации шума, вносимого усилителем в сигнал. Для этого используются специальные малошумящие усилители , которые могут быть как низкоомные, например, на биполярных транзисторах, так и высокоомными на полевых транзисторах, однако спроектированы они таким образом, что наименьший коэффициент шума достигается лишь при полном согласовании выходного сопротивления источника сигнала и входного сопротивления самого усилителя. Например, если источник сигнала обладает меньшим выходным сопротивлением (например, микрофон с выходным сопротивлением 30 Ом), то следует применить между источником и усилителем повышающий трансформатор , который повысит выходное сопротивление (а также напряжение сигнала) до необходимого значения.
Limitations
Понятие внутреннего сопротивления вводится через эквивалентную схему, поэтому имеют силу те же ограничения , что и для применимости эквивалентных схем.
Examples
Значения внутреннего сопротивления относительны: то, что считается малым, например, для гальванического элемента, является очень большим для мощного аккумулятора. Ниже приведены примеры двухполюсников и значения их внутреннего сопротивления r . Тривиальные случаи двухполюсников без источников оговорены особо.
Малое внутреннее сопротивление
- Нулевым внутренним сопротивлением обладает только идеальный генератор напряжения . Если также рассматривать двухполюсники без источников, то сверхпроводящее короткое соединение тоже имеет нулевое внутреннее сопротивление (до величины токов, вызывающих потерю сверхпроводимости). Генератор со сверхпроводящей обмоткой при не слишком больших частотах и небольших токах также имеет активное внутреннее сопротивление, весьма близкое к нулю (индуктивный импеданс при определенных условиях может быть тоже довольно невелик).
- Автомобильная свинцово-кислотная стартёрная аккумуляторная батарея имеет r около 0,01 Ом. Благодаря столь низкому внутреннему сопротивлению ток, отдаваемый батареей при запуске двигателя, достигает 250 ампер и более (для легковых автомобилей).
- Бытовая сеть электроснабжения переменного тока в жилых помещениях имеет r от десятых долей Ом до 1 Ом и более (зависит от качества электропроводки ). Высокое сопротивление соответствует плохой проводке: при подключении мощных нагрузок (например, утюга ) напряжение падает, при этом заметно уменьшается яркость ламп освещения, подключенных к той же ветви сети. Повышается пожароопасность , поскольку на сопротивлении проводов выделяется значительная мощность. И наоборот, в хорошей сети с низким сопротивлением напряжение падает от допустимых нагрузок лишь незначительно. Ток при коротком замыкании в хорошей бытовой электросети достигает нескольких сотен ампер.
- Using negative feedback in electronic circuits, it is possible to artificially create sources with (under certain conditions) very low internal resistance. These properties are possessed by modern electronic voltage stabilizers . For example, an integrated voltage regulator 7805 (output voltage 5 V) has a typical output impedance of less than 0.0009 Ohm [9] . However, this does not mean at all that such a stabilizer can give a load of up to 5500 A or power up to 13 kW with proper coordination. The characteristics of the stabilizer are normalized only for the operating range of currents, that is, in this example, up to 1.5 A. If this value is exceeded, the protection will work and the stabilizer will turn off (with other protection designs, the current is limited, but not completely turned off).
Great Inner Resistance
Typically, two-terminal devices with high internal resistance are various sensors, signal sources, etc. A typical task when working with such devices is to remove a signal from them without loss due to incorrect matching. To achieve good voltage matching, the signal from such a two-terminal device must be removed by a device having an even higher input impedance (as a rule, the signal from a high-impedance source is removed using a buffer amplifier ).
- Only the ideal current source has infinite internal resistance. If we also consider two-terminal devices without sources, then a simple open circuit (two terminals, not connected in any way) also has infinite internal resistance.
- Condenser microphones , piezoelectric and pyroelectric sensors, as well as all other “ condenser-like ” devices, have reactive internal resistance, the module of which can reach [10] tens and hundreds of megaohms . Therefore, such sources require the use of a buffer amplifier to achieve voltage matching. Condenser microphones, as a rule, already contain a built-in buffer amplifier assembled on a field-effect transistor .
- To measure the electric potentials inside living cells, electrodes are used , which are a glass capillary filled with a conductive liquid. The thickness of such a conductor may be of the order of hundreds of angstroms . Due to the extremely small thickness of the conductor, such a “two-terminal network” (a cell with attached electrodes) has an internal resistance of the order of 100 megohms. High resistance and low voltage make measuring stress within the cell a daunting task.
Negative Internal Resistance
There are two-terminal devices, the internal resistance of which has a negative value. In ordinary resistance, energy dissipation occurs, in reactance , energy is stored and then released back to the source. The peculiarity of negative resistance is that it itself is a source of energy. Therefore, negative resistance in its pure form does not occur, it can only be simulated by an electronic circuit, which necessarily contains an energy source. Negative internal resistance can be obtained in circuits by using:
- feedback
- elements with negative differential resistance , for example, tunnel diodes
Systems with negative resistance are potentially unstable and therefore can be used to build self-oscillators .
See also
Antenna Input Impedance
Links
- How does the internal battery resistance affect performance? (Eng.) How the internal resistance of a battery affects its performance.
- What is the internal resistance of a battery?
Literature
- Zernov N.V., Karpov V.G. Theory of radio circuits. - M. - L .: Energy, 1965. - 892 p.
- Jones M. Kh. Electronics - practical course. - M .: Technosphere, 2006 .-- 512 s. ISBN 5-94836-086-5
- Tildon H. Glisson. Introduction to Circuit Analysis and Design. - Springer, 2011 .-- P. 768. - ISBN 9789048194421 .
Notes
- ↑ Impedance is a generalization of the concept of resistance for the case of reactive elements. See Electrical impedance for more details.
- ↑ It is incorrect to apply Ohm's law in this formulation to two-terminal networks with internal sources; it is necessary to take into account the sources: U = Ir + ΣU int , where ΣU int is the algebraic sum of the EMF of internal sources.
- ↑ The absence of sources is expressed in the fact that the voltage at the terminals of a two-terminal device in the absence of load is zero. This also includes the case when there are sources, but do not affect the output voltage (“not connected anywhere”).
- ↑ Reza F., Seeley S. Modern analysis of electrical circuits Energy, M.-L., 1964, 480 p. with hell.
- ↑ The exception is the use of compensation stabilizers. For example, a two-terminal device containing a battery and an op-amp , in some section of the I – V characteristic, can have both arbitrarily small and negative output impedance - as long as there is enough excess energy in the battery to compensate.
- ↑ The same as voltage
- ↑ 7.6. ENERGY RELATIONS IN SINUSOIDAL CURRENT CHAINS . Date of treatment April 6, 2014.
- ↑ However, quenching resistors are widely used to limit the inrush current of DC traction motors in electric vehicles .
- ↑ The change in the output voltage is not more than 1.3 mV in the range of output currents 0.005 ÷ 1.5 A. In a narrower range of currents 0.25 ÷ 0.75 A, the typical output resistance is even less - 0.0003 ohms.
- ↑ In the operating frequency range