Injection (Math)

Injective function.

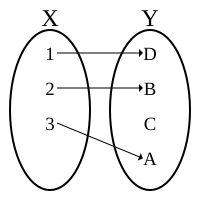
Math Injection - Mapping $f$ ${\ displaystyle f}$ $f$ many $X$ ${\ displaystyle X}$ $X$ in many $Y$ ${\ displaystyle Y}$ $Y$ ( $f\colon X\to Y$ ${\ displaystyle f \ colon X \ to Y}$ $f \ colon X \ to Y$ ), in which different elements of the set $X$ ${\ displaystyle X}$ $X$ translate into different elements of the set $Y$ ${\ displaystyle Y}$ $Y$ , that is, if two images coincide during the mapping, then the inverse images also coincide: $f(x)=f(y)\Rightarrow x=y$ ${\ displaystyle f (x) = f (y) \ Rightarrow x = y}$ $f (x) = f (y) \ Rightarrow x = y$ .

An injection is also called an attachment or a one-to-one mapping (as opposed to a bijection , which is one-to-one ). Unlike surjection , about which it is said that it maps one set onto another, about injection $f\colon X\to Y$ ${\ displaystyle f \ colon X \ to Y}$ $f \ colon X \ to Y$ a similar phrase is formulated as a mapping $X$ ${\ displaystyle X}$ $X$ at $Y$ ${\ displaystyle Y}$ $Y$ .

An injection can also be defined as a mapping for which there is a left inverse , that is, $f\colon X\to Y$ ${\ displaystyle f \ colon X \ to Y}$ $f \ colon X \ to Y$ injective if exists $g\colon Y\to X$ ${\ displaystyle g \ colon Y \ to X}$ $g \ colon Y \ to X$ at which $g\circ f=\operatorname {id} _{X}$ ${\ displaystyle g \ circ f = \ operatorname {id} _ {X}}$ $g \ circ f = \ operatorname {id} _X$ .

The concept of injection (along with surjection and bijection) was introduced in the writings of Bourbaki and became widespread in almost all branches of mathematics.

A generalization of the concept of injection in category theory is the concept of monomorphism , in many categories these concepts are equivalent, but this is not always true.

Examples:

$f\colon \mathbb {R} _{>0}\to \mathbb {R} ,\;f(x)=\ln x$ ${\ displaystyle f \ colon \ mathbb {R} _ {> 0} \ to \ mathbb {R}, \; f (x) = \ ln x}$ ${\ displaystyle f \ colon \ mathbb {R} _ {> 0} \ to \ mathbb {R}, \; f (x) = \ ln x}$ - injective and surjective.
$f\colon \mathbb {R} _{+}\to \mathbb {R} ,\;f(x)=x^{2}$ ${\ displaystyle f \ colon \ mathbb {R} _ {+} \ to \ mathbb {R}, \; f (x) = x ^ {2}}$ ${\ displaystyle f \ colon \ mathbb {R} _ {+} \ to \ mathbb {R}, \; f (x) = x ^ {2}}$ - injectively.
$f\colon \mathbb {R} \to \mathbb {R} ,\;f(x)=x^{2}$ ${\ displaystyle f \ colon \ mathbb {R} \ to \ mathbb {R}, \; f (x) = x ^ {2}}$ ${\ displaystyle f \ colon \ mathbb {R} \ to \ mathbb {R}, \; f (x) = x ^ {2}}$ - is not injective ( $f(-2)=f(2)=4$ ${\ displaystyle f (-2) = f (2) = 4}$ $f (-2) = f (2) = 4$ ).

One of the applied examples of applying the concept of injection is the organization of a one-to-one relationship between entities in a relational data model . Another example is perfect hashing .

Literature

N.K. Vereshchagin, A. Shen. Beginnings of set theory // Lectures on mathematical logic and theory of algorithms . (inaccessible link)
Ershov Yu. L., Palyutin E. A. Mathematical Logic: Study Guide. - 3rd, stereotype. ed. - SPb. : Doe, 2004 .-- 336 p.

Injection (Math)

Literature

See also

More articles: