Symmetric group

Cayley graph of the symmetric group S ₄

Cayley table of the symmetric group S ₃
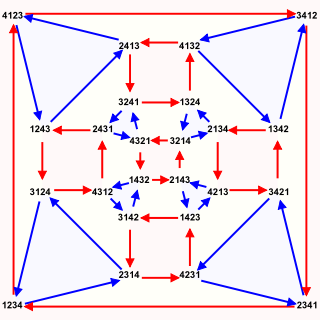
( permutation matrix multiplication table )

The following six matrix positions are available:

The table is asymmetric with respect to the main diagonal, i.e. the group is not abelian.

Symmetric group - the group of all permutations of a given set $X$ ${\ displaystyle X}$ $X$ (i.e. bijection $X\to X$ ${\ displaystyle X \ to X}$ $X \ to X$ ) relative to the operation of the composition .

The symmetric group of the set $X$ ${\ displaystyle X}$ $X$ usually indicated $S(X)$ ${\ displaystyle S (X)}$ $S (x)$ , if $X=\{1,2,...,n\}$ ${\ displaystyle X = \ {1,2, ..., n \}}$ $X = \ {1,2, ..., n \}$ then $S(X)$ ${\ displaystyle S (X)}$ $S (x)$ also denoted by $S_{n}$ ${\ displaystyle S_ {n}}$ $S_ {n}$ . Since for equipotent sets ( $|X|=|Y|$ ${\ displaystyle | X | = | Y |}$ $| X | = | Y |$ ) their permutation groups ( $S(X)\cong S(Y)$ ${\ displaystyle S (X) \ cong S (Y)}$ ${\ displaystyle S (X) \ cong S (Y)}$ ), therefore, for a finite group of order $n$ ${\ displaystyle n}$ $n$ the group of its permutations is identified with $S_{n}$ ${\ displaystyle S_ {n}}$ $S_ {n}$ .

The neutral element in the symmetric group is the identity permutation $\mathrm {id} (x)=x$ ${\ displaystyle \ mathrm {id} (x) = x}$ ${\ displaystyle \ mathrm {id} (x) = x}$ .

Content

1 permutation groups
2 Properties
3 views
4 notes
5 Literature

Permutation Groups

Although usually the group of permutations (or permutations) is called the symmetric group itself, sometimes, especially in English literature, permutation groups of the set $X$ ${\ displaystyle X}$ called subgroups of a symmetric group $S(X)$ ${\ displaystyle S (X)}$ ^[1] . The degree of the group in this case is called the power $X$ ${\ displaystyle X}$ .

Each end group $G$ ${\ displaystyle G}$ isomorphic to some subgroup of the group $S(G)$ ${\ displaystyle S (G)}$ ( Cayley's theorem ).

Properties

The number of elements of the symmetric group for a finite set is equal to the number of permutations of the elements, that is, the power factorial : $|S_{n}|=n!$ ${\ displaystyle | S_ {n} | = n!}$ . At $n\geqslant 3$ ${\ displaystyle n \ geqslant 3}$ symmetric group $S_{n}$ ${\ displaystyle S_ {n}}$ non-commutative.

Symmetric group $S_{n}$ ${\ displaystyle S_ {n}}$ allows the following task :

\langle \sigma _{1},\sigma _{2},\dots ,\sigma _{n-1}|\sigma _{i}^{2},(\sigma _{i}\sigma _{i+1})^{3},\sigma _{i}\sigma _{j}=\sigma _{j}\sigma _{i}\ {\text{if}}\ |i-j|>1\rangle

{\ displaystyle \ langle \ sigma _ {1}, \ sigma _ {2}, \ dots, \ sigma _ {n-1} | \ sigma _ {i} ^ {2}, (\ sigma _ {i} \ sigma _ {i + 1}) ^ {3}, \ sigma _ {i} \ sigma _ {j} = \ sigma _ {j} \ sigma _ {i} \ {\ text {if}} \ | ij | > 1 \ rangle}

.

We can assume that $\sigma _{i}$ ${\ displaystyle \ sigma _ {i}}$ rearranges $i$ ${\ displaystyle i}$ and $i+1$ ${\ displaystyle i + 1}$ . Maximum order of group elements $S_{n}$ ${\ displaystyle S_ {n}}$ - Landau function .

Groups $S_{1},S_{2},S_{3},S_{4}$ ${\ displaystyle S_ {1}, S_ {2}, S_ {3}, S_ {4}}$ solvable when $n\geqslant 5$ ${\ displaystyle n \ geqslant 5}$ symmetric group $S_{n}$ ${\ displaystyle S_ {n}}$ is insoluble .

A symmetric group is perfect (that is, the conjugation map is an isomorphism) if and only if its order is different from 2 and 6 ( Hölder's theorem ). When $n=6$ ${\ displaystyle n = 6}$ Group $S_{6}$ ${\ displaystyle S_ {6}}$ has another . By virtue of this and the previous property, for $n\geqslant 3,n\neq 6$ ${\ displaystyle n \ geqslant 3, n \ neq 6}$ all automorphisms $S_{n}$ ${\ displaystyle S_ {n}}$ are internal, that is, every automorphism $\alpha (x)$ ${\ displaystyle \ alpha (x)}$ has the form $g^{-1}xg$ ${\ displaystyle g ^ {- 1} xg}$ for some $g\in S_{n}$ ${\ displaystyle g \ in S_ {n}}$ .

The number of classes of conjugate elements of a symmetric group $S_{n}$ ${\ displaystyle S_ {n}}$ equal to the number of partitions $n$ ${\ displaystyle n}$ ^[2] . Many transpositions $(12),(23),...,(n-1\ n)$ ${\ displaystyle (12), (23), ..., (n-1 \ n)}$ is the generating set $S_{n}$ ${\ displaystyle S_ {n}}$ . On the other hand, all these transpositions are generated by just two permutations $(12),(12...n)$ ${\ displaystyle (12), (12 ... n)}$ so that the minimum number of generators of a symmetric group is two.

The center of the symmetric group is trivial for $n\geqslant 3$ ${\ displaystyle n \ geqslant 3}$ . Commutant $S_{n}$ ${\ displaystyle S_ {n}}$ is an alternating group $A_{n}$ ${\ displaystyle A_ {n}}$ ; with $n\neq 4$ ${\ displaystyle n \ neq 4}$ $A_{n}$ ${\ displaystyle A_ {n}}$ Is the only nontrivial normal subgroup $S_{n}$ ${\ displaystyle S_ {n}}$ , but $S_{4}$ ${\ displaystyle S_ {4}}$ has another normal subgroup - the Klein quadruple group .

Views

Any subgroup $G$ ${\ displaystyle G}$ permutation groups $S_{n}$ ${\ displaystyle S_ {n}}$ representable by a group of matrices from $SL(n,\mathbb {Z} )$ ${\ displaystyle SL (n, \ mathbb {Z})}$ , with each permutation $\pi :i\to \pi (i)$ ${\ displaystyle \ pi: i \ to \ pi (i)}$ there corresponds a permutation matrix (a matrix in which all elements in cells $(i,\pi (i))$ ${\ displaystyle (i, \ pi (i))}$ equal to 1, and other elements are equal to zero); e.g. permutation $(231)$ ${\ displaystyle (231)}$ represented by the following matrix $3\times 3$ ${\ displaystyle 3 \ times 3}$ :

{\begin{pmatrix}0&1&0\\0&0&1\\1&0&0\end{pmatrix}}

{\ displaystyle {\ begin {pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \ end {pmatrix}}}

A subgroup of such a group, composed of matrices with determinant equal to 1, is isomorphic to an alternating group $A_{n}$ ${\ displaystyle A_ {n}}$ .

There are other representations of symmetric groups, for example, the symmetry group (consisting of rotations and reflections) of the dodecahedron is isomorphic $S_{5}$ ${\ displaystyle S_ {5}}$ , and the rotation group of the cube is isomorphic $S_{4}$ ${\ displaystyle S_ {4}}$ .

Notes

↑ Aigner M. Combinatorial Theory. M .: Mir, 1982.- 561 p.
↑ sequence A000041 in OEIS

Literature

Vinberg E. B. The course of algebra. - M .: Factorial Press, 2001.
Kargapolov M. I, Merzlyakov Yu.I. Fundamentals of group theory. - M .: Science, Fizmatlit, 1982.
Kostrikin A. I. Introduction to Algebra. Part III. The main structure. - M. publishing house = Fizmatlit, 2004.
Kurosh A.G. Group Theory. - M .: Science, Fizmatlit, 1967.
Postnikov M.M. Galois Theory. - M .: Fizmatlit, 1963.

[1] Aigner M. Combinatorial Theory. M .: Mir, 1982.- 561 p.

[2] sequence A000041 in OEIS