
A gear wheel or gear [1] , gear [2] - the main part of the gear in the form of a disk with teeth on a cylindrical or conical surface, which mesh with the teeth of another gear.
Typically, the terms gear , gear , gear are synonymous, but some authors call the leading gear wheel gear , and driven - wheel [2] . The origin of the word “gear” is not known for certain, although there are suggestions of a connection with the number “six”. L. V. Kurkina, however, derives the term from the word “pole” (in the sense of “ axis ”) [3] .
Gears are usually used in pairs with different numbers of teeth in order to convert the torque and the number of revolutions of the shafts at the input and output. The wheel to which torque is supplied from the outside is called the drive wheel, and the wheel from which the torque is removed is called the driven one . If the diameter of the drive wheel is smaller , then the torque of the driven wheel increases due to a proportional decrease in rotation speed , and vice versa . In accordance with the gear ratio , an increase in torque will cause a proportional decrease in the angular speed of rotation of the driven gear, and their product - mechanical power - will remain unchanged. This ratio is valid only for an ideal case that does not take into account friction losses and other effects characteristic of real devices.
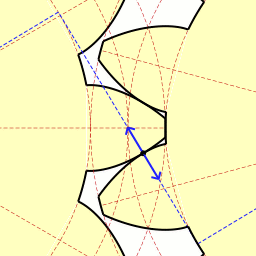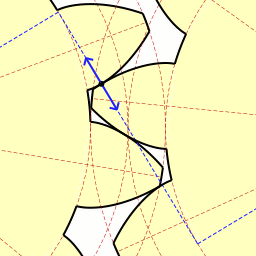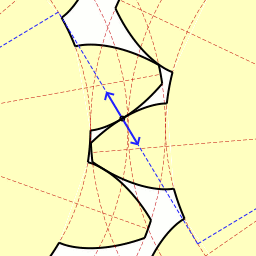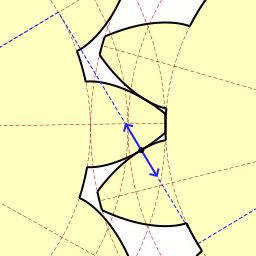
left - drive, right - driven wheel

Spur gears
The profile of the teeth of the wheels usually has an involute lateral shape . However, there are gears with a circular tooth profile ( Novikov gear with one and two lines of engagement) and cycloidal . In addition, ratchets use gears with an asymmetrical tooth profile.
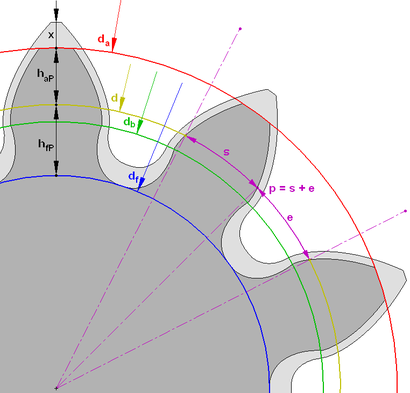
The parameters of the involute gear:
- m is the wheel module. A gearing module is a linear quantity π times smaller than the circumferential pitch P or the ratio of the pitch along any concentric circumference of the gear to π , i.e. the modulus is the number of millimeters of the diameter of the pitch circle per tooth. Dark and light wheels have the same module. The most important parameter, standardized , is determined from the strength calculation of gears. The more the gear is loaded, the higher the module value. Through it, all other parameters are expressed. The module is measured in millimeters , calculated by the formula:
- z is the number of teeth of the wheel
- p - tooth pitch (marked in purple)
- d - diameter of the pitch circle (marked in yellow)
- d a - the diameter of the circle of the vertices of the dark wheel (marked in red)
- d b - diameter of the main circle - involutes (marked in green)
- d f - diameter of the circumference of the depressions of the dark wheel (marked in blue)
- h aP + h fP - the height of the tooth of the dark wheel, x + h aP + h fP - the height of the tooth of the light wheel
In mechanical engineering, certain values of the gear module m are adopted for the convenience of manufacturing and replacing gears, which are integers or numbers with a decimal fraction: 0.5 ; 0.7 ; 1 ; 1.25 ; 1.5 ; 1.75 ; 2 ; 2.5 ; 3 ; 3.5 ; 4 ; 4,5 ; 5 and so on to 50 . (for more details see GOST 9563-60 Gear wheels. Modules)
The height of the tooth head - h aP and the height of the tooth leg - h fP - in the case of the so-called a zero gear (manufactured without offset, a gear with “zero” teeth) (the offset of the cutting rack cutting the teeth closer or further to the workpiece, the offset closer to the workpiece is called a negative offset , and the offset farther from the workpiece is called positive ) with module m as follows: h aP = m; h fP = 1.25 m , i.e.
From this we get that the height of the tooth h (not shown in the figure):
In general, it is clear from the figure that the diameter of the circumference of the peaks d a is greater than the diameter of the circumference of the depressions d f by the double tooth height h . Based on all this, if you need to practically determine the gear module m of the gear wheel, without the necessary data for calculations (except for the number of teeth z ), then it is necessary to accurately measure its outer diameter d a and divide the result by the number of teeth z plus 2:
Tooth line
Gears are classified depending on the shape of the longitudinal line of the tooth on:
- spur
- helical
- chevron
Spur gears
Spur gears are the most common type of gears. The teeth are located in radial planes, and the contact line of the teeth of both gears is parallel to the axis of rotation. In this case, the axes of both gears should also be located strictly parallel. Spur gears have the lowest cost, but at the same time, the ultimate torque of such wheels is lower than helical and chevron ones.
Helical gears
Helical gears are an improved version of spur gears. Their teeth are arranged at an angle to the axis of rotation, and form part of a helix in shape.
- Advantages:
- The gearing of such wheels is smoother than that of spur gears, and with less noise.
- The contact area is increased compared to a spur gear, so the ultimate torque transmitted by the gear pair is also greater.
- The disadvantages of helical wheels are the following factors:
- During the operation of the helical gear, a mechanical force arises along the axis, which necessitates the use of thrust bearings for installing the shaft;
- An increase in the area of friction of the teeth (which causes additional loss of power for heating), which is compensated by the use of special lubricants.
In general, helical gears are used in mechanisms that require the transmission of high torque at high speeds, or having severe noise restrictions.
Chevron wheels
The invention of chevron transmission is often attributed to Andre Citroen , but in fact he only bought a patent for a more advanced scheme, which was invented by a Polish self-taught mechanic [4] . The teeth of such wheels are made in the form of the letter “V” (or they are obtained by joining two helical wheels with an opposite tooth arrangement). Gears based on such gears are commonly referred to as “chevron gears”.
Chevron wheels solve the axial force problem. The axial forces of both halves of such a wheel are mutually compensated, so there is no need to install shafts on thrust bearings. In this case, the transmission is self-aligning in the axial direction, which is why in gearboxes with chevron wheels one of the shafts is mounted on floating bearings (usually on bearings with short cylindrical rollers).
Internal gears
With severe restrictions on the dimensions, in planetary gears, in gear pumps with internal gearing, in the drive of the tank turret, wheels with a gear rim cut from the inside are used. The rotation of the driving and driven wheels is made in one direction. In such a transmission, there is less friction loss, that is, higher efficiency.
Sector Wheels
A sector wheel is part of a conventional wheel of any type. Such wheels are used in cases where the link rotation is not required for a full revolution, and therefore it is possible to save on its dimensions.
Wheel gears
The transmission based on wheels with circular teeth ( Novikov transmission ) has even higher driving characteristics than helical gears - high load gearing ability, high smoothness and quiet operation. However, they are limited in use by reduced, under the same conditions, efficiency and service life, such wheels are noticeably more difficult to manufacture. The line of teeth in them is a circle of radius selected for specific requirements. The contact of the tooth surfaces occurs at one point on the line of engagement, parallel to the axles of the wheels.
Bevel gears
In many machines, the implementation of the required movements of the mechanism is associated with the need to transfer rotation from one shaft to another, provided that the axes of these shafts intersect. In such cases, a bevel gear is used. There are types of bevel wheels that differ in the shape of the tooth lines: with straight, tangential, circular and curved teeth. Bevel gears with a circular tooth, for example, are used in automotive final drives of a gearbox.
Rack gear (rack)
The rack and pinion transmission (rack) is used in cases where it is necessary to convert the rotational motion into translational and vice versa. It consists of a regular spur gear and a toothed bar (rack). The operation of such a mechanism is shown in the figure.
A gear rack is a part of a wheel with an infinite radius of a pitch circle. Therefore, the dividing circle, as well as the circles of the peaks and troughs, turn into parallel straight lines. The involute profile of the rail also takes a straight line. This property of involute was the most valuable in the manufacture of gears.
The rack and pinion gear is also used in the cog railway .
Crown Wheels
The crown wheel is a special kind of wheels whose teeth are located on the side surface. Such a wheel, as a rule, fits into a conventional spur gear, or with a drum of rods (pinwheel), as in a tower clock. Pinion gears are one of the earliest and easiest to manufacture, but have very large friction losses.
Others
Toothed drums of cinema equipment - designed to accurately move film over perforation . Unlike conventional gears meshed with other wheels or gear profiles, the gear drums of the movie equipment have a tooth pitch selected in accordance with the perforation pitch. Most of these drums have an involute tooth profile made using the same technologies as the rest of the gears.
Gear Making
Break-in method
It is currently the most technologically advanced, and therefore the most common method of manufacturing gears. In the manufacture of gears, tools such as a comb, a worm cutter and a cutter can be used.
Comb Testing Method
A cutting tool in the form of a rack is called a gear cutting comb. On one side of the comb, a cutting edge is sharpened along the contour of its teeth. The workpiece of the rolling wheel rotates around an axis. The comb performs complex movements, consisting of translational motion perpendicular to the axis of the wheel and reciprocating motion (not shown in the animation) parallel to the axis of the wheel to remove chips along the entire width of its rim. The relative motion of the comb and the workpiece may be different, for example, the workpiece may make an intermittent complex rolling movement, consistent with the movement of cutting the comb. The workpiece and the tool move relative to each other on the machine as if the profile of the cut teeth engages with the initial producing contour of the comb.
Worm cutter break-in method
In addition to the comb, a worm cutter is used as a cutting tool. In this case, worm gearing occurs between the workpiece and the milling cutter.
Break-in method using dolbyak
Cogwheels are also hollowed on gear - grinding machines using special cutters. The gear shaping cutter is a gear wheel equipped with cutting edges. Since it is usually impossible to cut off the entire metal layer at once, processing is carried out in several stages. During processing, the tool makes a reciprocating motion relative to the workpiece. After each double stroke, the workpiece and tool rotate about their axes by one step. Thus, the tool and the workpiece, as it were, “run in” on each other. After the workpiece makes a full revolution, the cutter makes a feed movement to the workpiece. This process occurs until all the necessary metal layer is removed.
Copy Method (Division Method)
A disk or a finger mill cuts one cavity of a gear wheel. The cutting edge of the tool has the shape of this cavity. After cutting one cavity, the workpiece is rotated by one angular step using a dividing device, the cutting operation is repeated.
The method was applied at the beginning of the 20th century . The disadvantage of this method is its low accuracy: the depressions of the wheels made by this method are very different from each other.
Hot and cold rolling
The process is based on successive deformation of a layer heated to a plastic state of a certain workpiece depth by a gear rolling tool. This combines the induction heating of the surface layer of the workpiece to a certain depth, the plastic deformation of the heated layer of the workpiece for the formation of teeth and the running of the formed teeth to obtain a given shape and accuracy.
Cone Wheel Making
The technology for the manufacture of bevel wheels is closely connected with the geometry of the side surfaces and tooth profiles. The method of copying the shaped profile of the tool to form the profile on the bevel wheel cannot be used, since the dimensions of the hollow of the bevel wheel change as you approach the top of the cone. In this regard, tools such as a modular disk mill, a finger mill, a shaped grinding wheel can only be used for rough cutting of cavities or for the formation of wheel cavities not higher than the eighth degree of accuracy.
For cutting more precise bevel wheels, a break-in method is used in machine engagement of the cut workpiece with an imaginary producing wheel. The lateral surfaces of the producing wheel are formed due to the movement of the cutting edges of the tool in the process of the main cutting movement, ensuring the cutting of the allowance . The predominant distribution has received tools with a straight blade. With a rectilinear main movement, a rectilinear blade forms a flat producing surface. Such a surface cannot form an involute conical surface with spherical involute profiles. The resulting conjugate conical surfaces that differ from involute surfaces are called quasi-involute.
Modeling
Ошибки при проектировании зубчатых колёс
Подрезание зуба
Согласно свойствам эвольвентного зацепления, прямолинейная часть исходного производящего контура зубчатой рейки и эвольвентная часть профиля зуба нарезаемого колеса касаются только на линии станочного зацепления. За пределами этой линии исходный производящий контур пересекает эвольвентный профиль зуба колеса, что приводит к подрезанию зуба у основания, а впадина между зубьями нарезаемого колеса получается более широкой. Подрезание уменьшает эвольвентную часть профиля зуба (что приводит к сокращению продолжительности зацепления каждой пары зубьев проектируемой передачи) и ослабляет зуб в его опасном сечении. Поэтому подрезание недопустимо. Чтобы подрезания не происходило, на конструкцию колеса накладываются геометрические ограничения, из которых определяется минимальное число зубьев, при котором они не будут подрезаны. Для стандартного инструмента это число равняется 17. Также подрезания можно избежать, применив способ изготовления зубчатых колёс, отличный от способа обкатки. Однако и в этом случае условия минимального числа зубьев нужно обязательно соблюдать, иначе впадины между зубьями меньшего колеса получатся столь тесными, что зубьям большего колеса изготовленной передачи будет недостаточно места для их движения и передача заклинится.
Для уменьшения габаритных размеров зубчатых передач колёса следует проектировать с малым числом зубьев. Поэтому при числе зубьев меньше 17, чтобы не происходило подрезания, колёса должны быть изготовлены со смещением инструмента — увеличением расстояния между инструментом и заготовкой ( корригированные зубчатые колеса).
Заострение зуба
При увеличении смещения инструмента толщина зуба будет уменьшаться. Это приводит к заострению зубьев. Опасность заострения особенно велика у колёс с малым числом зубьев (менее 17). Для предотвращения скалывания вершины заострённого зуба смещение инструмента ограничивают сверху.
В природе
Зубчатые передачи используются у личинок насекомых рода Issus для синхронизации движения ног в момент прыжка. [5] [6]
В геральдике
Зубчатое колесо и шестерёнка являются искусственными негеральдическими фигурами, которые получили очень широкое распространение в международной, территориальной и родовой геральдике. Эта эмблема появилась в эпоху машинного производства во второй половине XIX - начале XX века. Чаще всего зубчатое колесо олицетворяет промышленность, технический и научный прогресс, индустриализацию, модернизацию [7] . В послевоенные годы шестерню в СССР широко использовалось в муниципальной геральдике Советского Союза.
Изображения зубчатых колёс присутствуют на многих гербах , в числе которых:
Balashikha
Volgograd
Волновахский район
Забже
Изобильный
Kemerovo
Клявлинский район
Korolev
Kramatorsk
Московский район (Харьков)
Новоуральск
Октябрьский район (Харьков)
Pavlodar
Первомайск (город, Луганская область)
Первомайск (Нижегородская область)
Rubtsovsk
Свирск
Sysert
Стаханов
Усолье-Сибирское
Botswana
Italy
Laos
Избербаш
Устаревшие гербы:
Арсеньев
Lugansk
Карпинск
Kopeysk
Курган
Moscow
Nizhny Tagil
Нижняя Тура
Novosibirsk
Omsk
Pavlodar
Прохладный
Severodvinsk
Фролово
Kharkov
See also
- Зубчатая передача
- Механическая передача
- Вариатор
- Планетарная передача
- Механическая коробка переключения передач
- Автоматическая коробка переключения передач
- Мотор-редуктор
- Шестерённая клеть
Links
Notes
- ↑ Шестерня // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). - SPb. , 1890-1907.
- ↑ 1 2 В. А. Татаринов. История отечественного терминоведения. Московский лицей, 1994. С. 213.
- ↑ Л. В. Куркина. Этимологические заметки // Этимология 1974 . М. , «Наука». 1976. С. 46.
- ↑ 7 нововведений Андре Ситроена, изменивших автомобильный бизнес
- ↑ Юлия Смирнова. Самая древняя «шестеренка» обнаружена на ногах насекомых // Наука и жизнь. — 2013.
- ↑ The First Gear Discovered in Nature // Popular Mechanics
- ↑ Похлёбкин В. 257. ШЕСТЕРНЯ // Словарь международной символики и эмблематики. — 2001. — ISSN 5-7133-0869-3 .
Literature
- Зубчатые колеса // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). - SPb. , 1890-1907.
- Ed. Скороходова Е. А. Общетехнический справочник. — М. : Машиностроение, 1982. — С. 416.
- Гулиа Н. В., Клоков В. Г., Юрков С. А. Детали машин. — М. : Издательский центр «Академия», 2004. — С. 416. — ISBN 5-7695-1384-5 .
- Богданов В. Н., Малежик И. Ф., Верхола А. П. и др. Справочное руководство по черчению. — М. : Машиностроение, 1989. — С. 438—480. - 864 s. — ISBN 5-217-00403-7 .
- Анурьев В. И. Справочник конструктора-машиностроителя: В 3 т. / Под ред. И. Н. Жестковой. — 8-е изд., перераб. и доп.. — М. : Машиностроение, 2001. — Т. 2. — 912 с. — ISBN 5-217-02964-1 (5-217-02962-5), ББК 34.42я2, УДК 621.001.66 (035).
- Фролов К. В., Попов С. А., Мусатов А. К., Тимофеев Г. А., Никоноров В. А. Теория механизмов и механика машин / Колесников К. С. — Издание четвёртое, исправленное и дополненное. — М. : Издательство МГТУ им. Н. Э. Баумана , 2002. — Т. 5. — С. 452—453, 456-459, 463-466, 497-498. — 664 с. — (Механика в техническом университете). - 3000 copies. — ISBN 5-7038-1766-8 .
- Леонова Л. М., Чигрик Н. Н., Татаурова В. П. Зубчатые передачи. Элементы расчета и конструирования: Методические указания . — Омск: Изд-во ОмГТУ , 2005. — 45 с. (inaccessible link)