Lognormal distribution

Lognormal
Lognormal
	; μ = 0 Probability Density
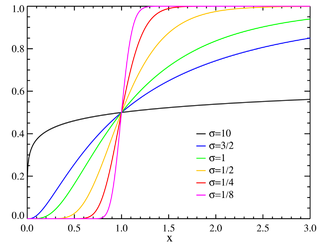	; μ = 0 distribution function
Designation	,
Options	;
Carrier
Probability density
Distribution function
Expected value
Median
Fashion
Dispersion
Asymmetry coefficient
Excess ratio
Differential entropy
The generating function of moments
Characteristic function

The lognormal distribution in probability theory is a two-parameter family of absolutely continuous distributions . If a random variable has a lognormal distribution, then its logarithm has a normal distribution .

Content

Definition

Let the distribution of a random variable $X$ ${\ displaystyle X}$ is given by the probability density , having the form:

f_{X}(x)={\frac {1}{x\sigma {\sqrt {2\pi }}}}e^{-(\ln x-\mu )^{2}/2\sigma ^{2}},

Where $x>0,\;\sigma >0,\;\mu \in \mathbb {R}$ ${\ displaystyle x> 0, \; \ sigma> 0, \; \ mu \ in \ mathbb {R}}$ . Then they say that $X$ ${\ displaystyle X}$ has a lognormal distribution with parameters $\mu$ ${\ displaystyle \ mu}$ and $\sigma$ ${\ displaystyle \ sigma}$ . They write: $X\sim \mathrm {LogN} (\mu ,\sigma ^{2})\$ ${\ displaystyle X \ sim \ mathrm {LogN} (\ mu, \ sigma ^ {2}) \}$ .

Moments

Formula for $k$ ${\ displaystyle k}$ of the lognormal random variable $X$ ${\ displaystyle X}$ has the form:

\mathbb {E} \left[X^{k}\right]=e^{k\mu +{\frac {k^{2}\sigma ^{2}}{2}}},\;k\in \mathbb {N} ,

{\ displaystyle \ mathbb {E} \ left [X ^ {k} \ right] = e ^ {k \ mu + {\ frac {k ^ {2} \ sigma ^ {2}} {2}}}, \ ; k \ in \ mathbb {N},}

whence in particular:

\mathbb {E} [X]=e^{\mu +{\sigma ^{2} \over 2}}

{\ displaystyle \ mathbb {E} [X] = e ^ {\ mu + {\ sigma ^ {2} \ over 2}}}

,

\mathrm {D} [X]=\left(e^{\sigma ^{2}}-1\right)e^{2\mu +\sigma ^{2}}

{\ displaystyle \ mathrm {D} [X] = \ left (e ^ {\ sigma ^ {2}} - 1 \ right) e ^ {2 \ mu + \ sigma ^ {2}}}

.

Any off-center moments of the n-dimensional joint lognormal distribution can be calculated using a simple formula:

\alpha _{n}=e^{(\mu ,n)+{\frac {1}{2}}(n,\Sigma n)}

{\ displaystyle \ alpha _ {n} = e ^ {(\ mu, n) + {\ frac {1} {2}} (n, \ Sigma n)}}

where

\mu

{\ displaystyle \ mu}

and

\Sigma

{\ displaystyle \ Sigma}

- parameters of multidimensional joint distribution.

n

{\ displaystyle n}

Is a vector whose components determine the order of the moment. (For example, in the two-dimensional case,

n=(2,0)

{\ displaystyle n = (2,0)}

- the second off-center moment of the first component,

n=(1,1)

{\ displaystyle n = (1,1)}

- mixed second moment). Parentheses denote a scalar product.

Lognormal Distribution Properties

If a $X_{1},\ldots ,X_{n}$ ${\ displaystyle X_ {1}, \ ldots, X_ {n}}$ Are independent lognormal random variables such that $X_{i}\sim \mathrm {LogN} (\mu ,\sigma _{i}^{2})$ ${\ displaystyle X_ {i} \ sim \ mathrm {LogN} (\ mu, \ sigma _ {i} ^ {2})}$ , then their product is also lognormal:
$Y=\prod \limits _{i=1}^{n}X_{i}\sim \mathrm {LogN} \left(n\mu ,\sum \limits _{i=1}^{n}\sigma _{i}^{2}\right)$ ${\ displaystyle Y = \ prod \ limits _ {i = 1} ^ {n} X_ {i} \ sim \ mathrm {LogN} \ left (n \ mu, \ sum \ limits _ {i = 1} ^ {n } \ sigma _ {i} ^ {2} \ right)}$ .

Relationship with other distributions

If a $X\sim \mathrm {LogN} (\mu ,\sigma ^{2})\$ ${\ displaystyle X \ sim \ mathrm {LogN} (\ mu, \ sigma ^ {2}) \}$ then $Y=\ln(X)\sim \mathrm {N} (\mu ,\sigma ^{2})\$ ${\ displaystyle Y = \ ln (X) \ sim \ mathrm {N} (\ mu, \ sigma ^ {2}) \}$ .

And vice versa, if $Y\sim \mathrm {N} (\mu ,\sigma ^{2})\$ ${\ displaystyle Y \ sim \ mathrm {N} (\ mu, \ sigma ^ {2}) \}$ then $X=\exp(Y)\sim \mathrm {LogN} (\mu ,\sigma ^{2})\$ ${\ displaystyle X = \ exp (Y) \ sim \ mathrm {LogN} (\ mu, \ sigma ^ {2}) \}$ .

Modeling Lognormal Random Variables

For modeling, a link with a normal distribution is usually used. Therefore, it is enough to generate a normally distributed random variable, for example, using the Box-Muller transform , and calculate its exponent.

Variations generalization

Lognormal distribution is a special case of the so-called Captain distribution .

Applications

The lognormal distribution satisfactorily describes the distribution of particle frequencies by their sizes during random crushing, for example hailstones in a hail , etc. However, there are exceptions, for example, the size distribution of asteroids in the solar system has a logarithmic distribution .

Literature

Crow, Edwin L. & Shimizu, Kunio (Editors) (1988), Lognormal Distributions, Theory and Applications , vol. 88, Statistics: Textbooks and Monographs, New York: Marcel Dekker, Inc., p. xvi + 387, ISBN 0-8247-7803-0
Aitchison, J. and Brown, JAC (1957) The Lognormal Distribution , Cambridge University Press.
Limpert, E; Stahel, W; Abbt, M. Lognormal distributions across the sciences: keys and clues (English) // BioScience : journal. - 2001. - Vol. 51 , no. 5 . - P. 341-352 . - DOI : 10.1641 / 0006-3568 (2001) 051 [0341: LNDATS] 2.0.CO; 2 .
Eric W. Weisstein et al. Log Normal Distribution at MathWorld . Electronic document, retrieved October 26, 2006.
Holgate, P. The lognormal characteristic function (neopr.) // Communications in Statistics - Theory and Methods. - 1989. - T. 18 , No. 12 . - S. 4539–4548 . - DOI : 10.1080 / 03610928908830173 .
Brooks, Robert; Corson, Jon; Donal, Wales . The Pricing of Index Options When the Underlying Assets All Follow a Lognormal Diffusion // Advances in Futures and Options Research: journal. - 1994. - Vol. 7 .

Lognormal
μ = 0 Probability Density
μ = 0 distribution function
Designation	$\ln N(\mu ,\sigma ^{2})$ ${\ displaystyle \ ln N (\ mu, \ sigma ^ {2})}$ ${\ displaystyle \ ln N (\ mu, \ sigma ^ {2})}$ , $LN(\mu ,\sigma ^{2})$ ${\ displaystyle LN (\ mu, \ sigma ^ {2})}$ ${\ displaystyle LN (\ mu, \ sigma ^ {2})}$
Options	$\sigma >0$ ${\ displaystyle \ sigma> 0}$ ${\ displaystyle \ sigma> 0}$ $-\infty <\mu <\infty$ ${\ displaystyle - \ infty <\ mu <\ infty}$ ${\ displaystyle - \ infty <\ mu <\ infty}$
Carrier	$x\in (0;+\infty )$ ${\ displaystyle x \ in (0; + \ infty)}$ ${\ displaystyle x \ in (0; + \ infty)}$
Probability density	$\exp \left(-\left.\left[{\frac {\ln(x)-\mu }{\sigma }}\right]^{2}\right/2\right)\left/\left(x\sigma {\sqrt {2\pi }}\right)\right.$ ${\ displaystyle \ exp \ left (- \ left. \ left [{\ frac {\ ln (x) - \ mu} {\ sigma}} \ right] ^ {2} \ right / 2 \ right) \ left / \ left (x \ sigma {\ sqrt {2 \ pi}} \ right) \ right.}$ $\ exp \ left (- \ left. \ left [{\ frac {\ ln (x) - \ mu} {\ sigma}} \ right] ^ {2} \ right / 2 \ right) \ left / \ left ( x \ sigma {\ sqrt {2 \ pi}} \ right) \ right.$
Distribution function	${\frac {1}{2}}+{\frac {1}{2}}\mathrm {Erf} \left[{\frac {\ln(x)-\mu }{\sigma {\sqrt {2}}}}\right]$ ${\ displaystyle {\ frac {1} {2}} + {\ frac {1} {2}} \ mathrm {Erf} \ left [{\ frac {\ ln (x) - \ mu} {\ sigma {\ sqrt {2}}}} \ right]}$ ${\ frac {1} {2}} + {\ frac {1} {2}} {\ mathrm {Erf}} \ left [{\ frac {\ ln (x) - \ mu} {\ sigma {\ sqrt {2}}}} \ right]$
Expected value	$e^{\mu +\sigma ^{2}/2}$ ${\ displaystyle e ^ {\ mu + \ sigma ^ {2} / 2}}$ $e ^ {{\ mu + \ sigma ^ {2} / 2}}$
Median	$e^{\mu }$ ${\ displaystyle e ^ {\ mu}}$ $e ^ {{\ mu}}$
Fashion	$e^{\mu -\sigma ^{2}}$ ${\ displaystyle e ^ {\ mu - \ sigma ^ {2}}}$ $e ^ {{\ mu - \ sigma ^ {2}}}$
Dispersion	$(e^{\sigma ^{2}}\!\!-1)e^{2\mu +\sigma ^{2}}$ ${\ displaystyle (e ^ {\ sigma ^ {2}} \! \! - 1) e ^ {2 \ mu + \ sigma ^ {2}}}$ $(e ^ {{\ sigma ^ {2}}} \! \! - 1) e ^ {{2 \ mu + \ sigma ^ {2}}}$
Asymmetry coefficient	$(e^{\sigma ^{2}}\!\!+2){\sqrt {e^{\sigma ^{2}}\!\!-1}}$ ${\ displaystyle (e ^ {\ sigma ^ {2}} \! \! + 2) {\ sqrt {e ^ {\ sigma ^ {2}} \! \! - 1}}}$ $(e ^ {{\ sigma ^ {2}}} \! \! + 2) {\ sqrt {e ^ {{\ sigma ^ {2}}} \! \! - 1}}$
Excess ratio	$e^{4\sigma ^{2}}\!\!+2e^{3\sigma ^{2}}\!\!+3e^{2\sigma ^{2}}\!\!-6$ ${\ displaystyle e ^ {4 \ sigma ^ {2}} \! \! + 2e ^ {3 \ sigma ^ {2}} \! \! + 3e ^ {2 \ sigma ^ {2}} \! \! -6}$ $e ^ {{4 \ sigma ^ {2}}} \! \! + 2e ^ {{3 \ sigma ^ {2}}}!! \! + 3e ^ {{2 \ sigma ^ {2}}} \ ! \! - 6$
Differential entropy	${\frac {1}{2}}+{\frac {1}{2}}\ln(2\pi \sigma ^{2})+\mu$ ${\ displaystyle {\ frac {1} {2}} + {\ frac {1} {2}} \ ln (2 \ pi \ sigma ^ {2}) + \ mu}$ ${\ frac {1} {2}} + {\ frac {1} {2}} \ ln (2 \ pi \ sigma ^ {2}) + \ mu$
The generating function of moments	$\operatorname {E} [X^{s}]=e^{s\mu +{\tfrac {1}{2}}s^{2}\sigma ^{2}}.$ ${\ displaystyle \ operatorname {E} [X ^ {s}] = e ^ {s \ mu + {\ tfrac {1} {2}} s ^ {2} \ sigma ^ {2}}.}$ $\ operatorname {E} [X ^ {s}] = e ^ {{s \ mu + {\ tfrac {1} {2}} s ^ {2} \ sigma ^ {2}}}.$
Characteristic function	$\sum _{n=0}^{\infty }{\frac {(it)^{n}}{n!}}e^{n\mu +n^{2}\sigma ^{2}/2}$ ${\ displaystyle \ sum _ {n = 0} ^ {\ infty} {\ frac {(it) ^ {n}} {n!}} e ^ {n \ mu + n ^ {2} \ sigma ^ {2 } / 2}}$ $\ sum _ {{n = 0}} ^ {{\ infty}} {\ frac {(it) ^ {n}} {n!}} e ^ {{n \ mu + n ^ {2} \ sigma ^ {2} / 2}}$