Saddle point

The saddle point of the function z = x ² -y ² (marked in red)

The saddle point on the height map (the center of the "eight" formed by contours)

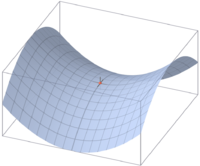
A saddle point in mathematical analysis is such a point from the domain of definition of a function that is stationary for a given function , but is not its local extremum . At such a point, if the function of two variables is considered, the surface formed by the function graph usually resembles a saddle or mountain pass in shape - convex in one direction and concave in the other. On a height map, a saddle point can generally be found at the intersection of contours . For example, two hills, between which there is a high pass , form a saddle point at the top of this pass : on the height map, it will look like the center of the “eight” formed by the corresponding contours .

Saddle Point in Mathematical Analysis

It is possible to check whether a given stationary point of the function F ( x , y ) of two variables is saddle, by calculating the Hessian matrix of the function at this point: if the Hessian is an indefinite quadratic form , then this point is a saddle. For example, composing a Hessian matrix of a function $z=x^{2}-y^{2}$ ${\ displaystyle z = x ^ {2} -y ^ {2}}$ at a stationary point $(0,0)$ ${\ displaystyle (0,0)}$ we get the matrix:

{\begin{bmatrix}2&0\\0&-2\\\end{bmatrix}}

{\ displaystyle {\ begin {bmatrix} 2 & 0 \\ 0 & -2 \\\ end {bmatrix}}}

which is uncertain. Therefore, the point $(0,0)$ ${\ displaystyle (0,0)}$ This function is saddle. However, the above criterion provides only a sufficient condition for the presence of a saddle point. For example, $(0,0)$ ${\ displaystyle (0,0)}$ is the saddle point of a function $z=x^{4}-y^{4}$ ${\ displaystyle z = x ^ {4} -y ^ {4}}$ , but the Hessian matrix in this case will be a zero matrix, which, by definition, cannot be called indefinite.

In the general case, the saddle point of a smooth function (whose graph depicts a curve , surface or hypersurface ) is a stationary point in the vicinity of which a given curve / surface / hypersurface does not lie completely on one side of the tangent space at a given point.

Graph y = x ³ with saddle point at 0

In the case of a function of one variable, a saddle point is a point that is both a stationary point and an inflection point (the inflection point is not a local extremum ).

Literature

Gray, Lawrence F .; Flanigan, Francis J .; Kazdan, Jerry L. & Frank, David H (1990), Calculus two: linear and nonlinear functions , Berlin: Springer-Verlag, p. page 375, ISBN 0-387-97388-5
Hilbert D., Kon-Vossen S. , Visual Geometry. - URSS, Per. with it., Vol. 5, 2010.344
von Petersdorff, Tobias (2006), "Critical Points of Autonomous Systems" , Differential Equations for Scientists and Engineers (Math 246 lecture notes) , < http://www.wam.umd.edu/~petersd/stab.html > . Retrieved November 12, 2009. Archived January 3, 2007 on Wayback Machine
Widder, DV (1989), Advanced calculus , New York: Dover Publications, p. page 128, ISBN 0-486-66103-2

Saddle point

Saddle Point in Mathematical Analysis

See also

Literature

More articles: