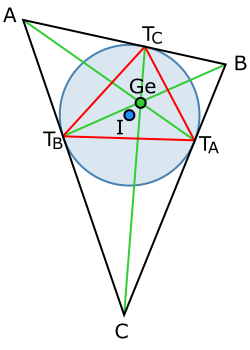
The triangle ΔABC, with an inscribed circle (blue), the center of the inscribed circle I, a red triangle built on the tangency points T a , T b and T c and the Gergonne point (green, Ge)
The point of Gergonne is the point of intersection of the segments connecting the vertices of the triangle with the points of tangency of opposite sides with an inscribed circle .
Usually denoted by , , or .
Content
Properties
- The Gergonne point is a Lemoine point of a triangle formed by the points of tangency of the sides of a triangle with an inscribed circle.
- The Gergonne point is isotomically conjugate to the Nagel point .
- The Gergonne point isogonally conjugate with the center of the negative homothety of the inscribed and circumscribed circle .
- The squared distance from the Gerlonn point to the center of the inscribed circle is
- The squared distance from the point of Gergonne to the center of the circumscribed circle is
- The point of Gergonne lies inside an open orthocentro circle with a punctured center. [one]
- A complete set of properties of the Gergonne point can be found in the Dekoff article. [2]
Gergonne Triangle
The Gergonne Triangle (for a triangle ABC ) is determined by three points of tangency of the inscribed circle on three sides. These vertices are denoted by T A , T B, and T C. Point T A lies opposite vertex A. This Gergonne triangle T T T T T C is also known as the triangle of tangencies of the triangle ABC .
Properties
- Three straight lines AT A , BT B and CT C intersect at one point - the Gergonne point and are denoted by Ge - X (7) .
- The point of the triangle of Gergonne is the intersection point of the Symmedians of the triangle of Gergonne .
- Suppose that the tangency points of the circle inscribed in a given triangle are connected by segments, then the Gergonne triangle is obtained, and the heights are drawn in the resulting triangle. In this case, the straight lines connecting the bases of these heights are parallel to the sides of the original triangle. Consequently, the orthotriangle of the Gergonne triangle and the original triangle are similar.
- The Gergonne Triangle (for a triangle ABC ) is a sugary triangle for the center of the triangle ABC .
See also
- Great Triangle Points
- Externally written circle
- Inscribed and excerpted in a triangle circle
- Circumcircle
- Nagel Point
History
The point of Gergonne was discovered by Joseph Diaz Gergonne, 06/19/1771 - 04.05.1859) at the beginning of the 19th century .
Notes
- ↑ Christopher J. Bradley, Geoff C. Smith. The locations of triangle centers // Forum Geometricorum. - 2006. - Vol. 6 - pp. 57-70. .
- ↑ Deko Dekov. Computer-generated Mathematics: The Gergonne Point // Journal of Computer-generated Euclidean Geometry. - 2009. - Vol . 1 . - P. 1–14. . Archived November 5, 2010.



