Ultrafilter

The yellow filter is a non-ultrafilter filter. When green elements are added to it, an ultrafilter is formed.

Ultrafilter on the grid $F$ ${\ displaystyle F}$ $F$ - This is the maximum own filter . The concept of ultrafilter appeared in the general topology , where it is used to generalize the concept of convergence on spaces with uncountable base.

Definition

Own filter $F$ ${\ displaystyle F}$ $F$ on the grill $L$ ${\ displaystyle L}$ $L$ is an ultrafilter if it is not contained in any of its own (that is, different from $F$ ${\ displaystyle F}$ $F$ ) filter.

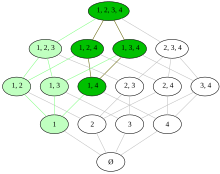
Set $F$ ${\ displaystyle F}$ $F$ subsets of the set $X$ ${\ displaystyle X}$ $X$ called ultrafilter on $X$ ${\ displaystyle X}$ $X$ , if a

$\varnothing \notin F$ ${\ displaystyle \ varnothing \ notin F}$ $\varnothing\notin F$
for any two items $F$ ${\ displaystyle F}$ $F$ their intersection also lies in $F$ ${\ displaystyle F}$ $F$
for any item $F$ ${\ displaystyle F}$ $F$ , all its supersets lie in $F$ ${\ displaystyle F}$ $F$
for any subset $Y\subseteq X$ ${\ displaystyle Y \ subseteq X}$ $Y \subseteq X$ or $Y\in F$ ${\ displaystyle Y \ in F}$ $Y \in F$ either $X\backslash Y\in F$ ${\ displaystyle X \ backslash Y \ in F}$ $X \backslash Y \in F$

In other words, if we consider a function on sets $S\subset X$ ${\ displaystyle S \ subset X}$ $S\subset X$ given as $\omega _{F}(S)=1$ ${\ displaystyle \ omega _ {F} (S) = 1}$ $\omega _{F}(S)=1$ , if a $S\in F$ ${\ displaystyle S \ in F}$ $S\in F$ and $\omega _{F}(S)=0$ ${\ displaystyle \ omega _ {F} (S) = 0}$ $\omega _{F}(S)=0$ otherwise then $\omega _{F}$ ${\ displaystyle \ omega _ {F}}$ $\omega _{F}$ is a finitely additive probability measure on $X$ ${\ displaystyle X}$ $X$ .

Ultrafilters in Boolean Algebras

If the lattice $L$ ${\ displaystyle L}$ $L$ is Boolean algebra , then the following characterization of ultrafilters is possible: filter $F$ ${\ displaystyle F}$ $F$ is an ultrafilter if and only if for any element $x\in L$ ${\ displaystyle x \ in L}$ $x\in L$ or $x\in F$ ${\ displaystyle x \ in F}$ $x \in F$ either $-x\in F$ ${\ displaystyle -x \ in F}$ $-x \in F$

This characterization makes ultrafilters look like complete theories .

Examples

any main filter is an ultrafilter
a subset of the Lindenbaum – Tarski algebra of the complete theory $T$ ${\ displaystyle T}$ $T$ consisting of theorems $T$ ${\ displaystyle T}$ $T$

Properties

an ultrafilter on a finite set is always prime .
Any ultrafilter on an infinite set contains a finite filter .
if a $F$ ${\ displaystyle F}$ - the main ultrafilter on the set $X$ ${\ displaystyle X}$ then its main element is the intersection of all elements of the ultrafilter.
if a $F$ ${\ displaystyle F}$ - non-main ultrafilter on set $X$ ${\ displaystyle X}$ , then the intersection of all its elements is empty.
Each filter is contained in the ultrafilter.
- This statement cannot be proved without using the axiom of choice .
- Also this statement is equivalent to the theorem on Boolean prime ideals .
- An important consequence of this theorem is the existence of non-principal ultrafilters on infinite sets.
Stone - Cech compactification of discrete space $X$ ${\ displaystyle X}$ - this is a set of ultrafilters on a lattice of subsets $X$ ${\ displaystyle X}$ endowed with Stone's topology . As the base of the open sets of the Stone topology on the set of ultrafilters $G$ ${\ displaystyle G}$ can take sets $D_{a}=\{U\in G|a\in U\}$ ${\ displaystyle D_ {a} = \ {U \ in G | a \ in U \}}$ for all kinds of $a\in P(X).$ ${\ displaystyle a \ in P (X).}$

Applications

Ultrafilters are used in a number of constructions of the theory of models , namely, to formulate the concept of ultra-production .
Ultrafilters also appear in the formulation of Stone's theorem on the representation of Boolean algebras and in the explicit construction of the Stone – Cech compactification .
Ultra-limit for metric spaces - generalization of Gromov – Hausdorf convergence