Equality of classes P and NP

Millennium Challenges
	Equality of classes P and NP
	Hodge hypothesis
	Poincare conjecture (solved)
	Riemann hypothesis
	Equation solution ; quantum theory ; Young - Mills
	Existence and smoothness ; solving equations ; Navier - Stokes
	Hypothesis ; Birch - Swinnerton Dyer

The question of the equality of complexity classes P and NP (also known as enumeration problem ^[1] ^[2] in Russian sources) is one of the central open problems of algorithm theory for more than three decades. If an affirmative answer is given to it, this will mean that it is theoretically possible to solve many complex problems much faster than now.

The relations between the classes P and NP are considered in the section of the theory of algorithms, which is called the theory of computational complexity . She studies the resources necessary to solve a problem. The most common resources are time (how many steps are needed) and memory (how much memory is needed to solve the problem).

The problem of the equality of the classes P and NP is one of the seven problems of the millennium , for the solution of which the Clay Institute of Mathematics appointed a prize of one million US dollars .

A similar problem exists in the theory of algebraic complexity for the classes VP and VNP ^[3] .

Wording

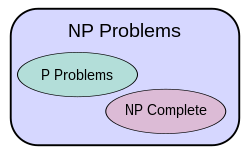
The diagram of complexity classes under the condition P ≠ NP .

It is not easy to say that the equality problem P = NP consists in the following: if a positive answer to a question can be checked quite quickly (in polynomial time ), is it true that the answer to this question can be found quite quickly (also in polynomial time and using polynomial memory )? In other words, is it really not easier to verify a solution to a problem than to find it? ^[four]

For example, is it true that among the numbers { −2 , −3 , 15 , 14 , 7 , −10 , ...} there are such that their sum is 0 (the problem of the sums of subsets)? The answer is yes , because −2 −3 + 15 −10 = 0 is easily verified by several additions (the information necessary to verify a positive answer is called a certificate ). Does it follow that it is just as easy to pick up these numbers? Verifying a certificate is as easy as finding it? It seems that picking up numbers is harder, but this is not proven.

The corollary immediately follows from the definition of the classes P and NP : $P\subseteq NP$ ${\ displaystyle P \ subseteq NP}$ $P \subseteq NP$ . However, so far nothing is known about the rigor of this inclusion, that is, whether there exists a problem lying in NP but not lying in P. If such a problem does not exist, then all problems belonging to the class NP can be solved in polynomial time, which promises enormous benefits in the speed of calculations. Now the most complex problems from the NP class (the so-called NP- complete problems ) can be solved in exponential time, which is considered unacceptable from a practical point of view.

History

Probably the first question about computational complexity was asked by Kurt Gödel in 1956 in a letter to John von Neumann , where he asked whether a certain problem (which, as is now known, is NP-complete) can be solved in quadratic or linear time. At the same time, Gödel suggested that if a solution exists, then this will solve many mathematical problems using computers ^[5] .

The question of class equality was first raised by Stephen Cook in 1971 ^[6] and, independently, by Leonid Levin in 1973 ^[7] .

At the beginning of the 2000s. most mathematicians believe that these classes are not equal. According to a survey conducted in 2002 among 100 scientists, ^[8] 61 people believe that the answer is “not equal,” 9 are “equal,” 22 found it difficult to answer and 8 believed that the hypothesis is not deducible from the current system of axioms and, therefore, thus cannot be proven or disproved.

Like other known unsolved mathematical problems, attempts to solve this problem attract considerable effort; erroneous proofs of equality or inequality of classes P and NP are regularly published (not in the scientific literature), usually by lay people ^[9] .

Protection systems involving class P and NP inequalities

Any public-key cryptosystem is based on the assumption of the existence of one-way functions and / or the extreme duration of solving a certain problem (for example, for the RSA algorithm this is a factorization of very large numbers).

To protect computer systems from abuse of services, the requesting party is asked to solve a problem that requires a lot of time to find a solution, and the result is easily and quickly checked by the service provider. An example of such anti- spam protection is the Hashcash system ^[10] , which uses a partial inversion hash when sending email.

In blockchains based on proof-of-work technology, the resulting hash amount should be less than the target value. The process of finding the desired hash sum requires its multiple conversion with enumeration of arbitrary values of an additional parameter (for more details, see Mining ). All computers in the system spend considerable time searching for one satisfactory hash sum (for example, in “ Bitcoin ” this takes an average of 10 minutes). To verify the correctness of an already formed block, only a single hash calculation is required.

Display in Art

The second series of the second season of the Elementary series describes potential problems that may arise if a solution to the equality of classes P and NP is successfully found for applied cases.
In the second series of the first season of the series "Numbers", one of the main characters tried to solve this problem.
In the series “ Futurama ”, you can notice the folder with the title “P = NP”.
In the series “Trace” (series 1358), the murder of a professor who is trying to solve the problem of equality of classes P and NP is investigated.
In the Minecraft computer game, in the main menu, the inscription sometimes appears: “NP is not in P” ^[11] .
In a series of books by Charles Strauss, Laundry Dossier, Alan Turing allegedly showed that the classes P and NP were equal. Since this made the tasks of computational magic and demonology easily solvable, he himself was killed by disguising his death as suicide, and his work was classified before it went to mass print.

Notes

↑ A.A. Razborov. P? = NP or brute force problem: a look from the 90s .
↑ A.H. Shen . The problem of busting // PostScience .
↑ Debriefing, 2016 , p. 24.
↑ Stuart, 2015 , p. 291.
↑ Hartmanis, Juris. Gödel, von Neumann, and the P = NP problem (neopr.) // Bulletin of the European Association for Theoretical Computer Science. - T. 38 . - S. 101-107 .
↑ Stephen Cook. The Importance of the P versus NP Question .
↑ L.A. Levin. Universal tasks of enumeration (rus.) // Problems of information transfer. - 1973. - T. 9 , No. 3 . - S. 115-116 .
↑ William I. Gasarch. The P =? NP poll (unopened) // SIGACT News. - 2002. - T. 33 , No. 2 . - S. 34–47 . - DOI : 10.1145 / 1052796.1052804 .
↑ Lenta.ru - Past. Mathematicians finally disbelieved in solving the millennium problem
↑ Hashcash - A Denial of Service Counter-Measure (2002)
↑ Splash - Official Minecraft Wiki

Literature

Ian Stewart . The greatest math problems. - M .: Alpina non-fiction, 2015 .-- 460 p. - ISBN 978-5-91671-318-3 .
John Hopcroft , Rajeev Motwani, Jeffrey Ullman. Introduction to Automata Theory, Languages, and Computation. - M .: "Williams" , 2002. - 528 p. - ISBN 0-201-44124-1 .
Razborov A.A. Algebraic complexity. - M .: ICMMO , 2016 .-- 32 p. - ISBN 978-5-4439-1032-1 .

Links

S. Cook Formal Description of the Problem
S. Nikolenko "P =? NP" . Computerra, 2006.
N.P. Warnowski. Problem P =? NP, complexity classes and cryptography . 2005.
Pritykin Yu. L. What is the problem P vs. Np? // VIII Summer School "Contemporary Mathematics". - Dubna, 2008.
Gerhard J. Woeginger. The P-versus-NP page . (English) List of links to the proposed "solutions" to this problem until 2016. Some of them claim the equality of P and NP , some - the opposite.
Scott Aaronson. Reasons to believe that P! = NP
Scott Aaronson . ${\color {MidnightBlue}{\mathsf {P}}{\stackrel {?}{=}}{\mathsf {NP}}}$ ${\ displaystyle {\ color {MidnightBlue} {\ mathsf {P}} {\ stackrel {?} {=}} {\ mathsf {NP}}}}$ - 2017 review.

[1] A.A. Razborov. P? = NP or brute force problem: a look from the 90s .

[2] A.H. Shen . The problem of busting // PostScience .

[_37d01e95ec89fbbd-3] Debriefing, 2016 , p. 24.

[_60c5fd3085a0d3d0-4] Stuart, 2015 , p. 291.

[5] Hartmanis, Juris. Gödel, von Neumann, and the P = NP problem (neopr.) // Bulletin of the European Association for Theoretical Computer Science. - T. 38 . - S. 101-107 .

[6] Stephen Cook. The Importance of the P versus NP Question .

[7] L.A. Levin. Universal tasks of enumeration (rus.) // Problems of information transfer. - 1973. - T. 9 , No. 3 . - S. 115-116 .

[8] William I. Gasarch. The P =? NP poll (unopened) // SIGACT News. - 2002. - T. 33 , No. 2 . - S. 34–47 . - DOI : 10.1145 / 1052796.1052804 .

[fail-9] Lenta.ru - Past. Mathematicians finally disbelieved in solving the millennium problem

[10] Hashcash - A Denial of Service Counter-Measure (2002)

[11] Splash - Official Minecraft Wiki