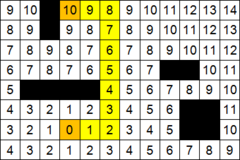

The wave trace algorithm ( wave algorithm , Lie algorithm ) is a path search algorithm, a shortest path search algorithm on a planar graph . Belongs to algorithms based on breadth-first search methods.
It is mainly used for computer tracing (wiring) of printed circuit boards , connecting conductors on the surface of microcircuits. Another application of the wave algorithm is the search for the shortest distance on the map in computer strategy games.
The wave algorithm in the context of finding a path in the maze was proposed by E. F. Moore [2] . Lee independently discovered the same algorithm when formalizing PCB trace algorithms in 1961 [3] [4] [5] .
Content
Algorithm Description
The algorithm operates on a discrete working field (DRP), which is a figure bounded by a closed line, not necessarily rectangular, broken into rectangular cells, in a particular case, square. The set of all DRP cells is divided into subsets: “passable” (free), that is, when searching for a path, they can pass, “impassable” (obstacles), the path through this cell is prohibited, the starting cell (source) and the finishing (receiver). The purpose of the start and finish cells is conditional, it’s enough to specify a pair of cells between which you need to find the shortest path.
The algorithm is designed to search for the shortest path from the starting cell to the final cell, if possible, or, in the absence of a path, issue a message about obstruction [6] .
The operation of the algorithm includes three stages: initialization , wave propagation and path restoration .
During initialization, an image of a plurality of cells of the processed field is built, attributes of patency / obstruction are attributed to each cell, the start and finish cells are remembered.
Further, a step to an adjacent cell is generated from the starting cell, and it is checked whether it is passable and does not belong to a cell previously labeled along the way.
It is customary to classify neighboring cells in two ways: in the sense of the Moore neighborhood and the von Neumann neighborhood , characterized in that in the von Neumann neighborhood only 4 cells are considered vertically and horizontally, in the Moore neighborhood - all 8 cells, including diagonal ones.
When the conditions of patency and its non-affiliation to the cells previously marked in the path are met, a number equal to the number of steps from the starting cell is written to the attribute of the cell, from the starting cell in the first step it will be 1. Each cell, marked with the number of steps from the starting cell, becomes the starting and next steps to neighboring cells are generated from it. Obviously, with such enumeration, the path from the initial cell to the final one will be found, or the next step from any cell generated in the path will be impossible.
The shortest path is restored in the opposite direction: when a cell is selected from the finishing cell to the starting one, at each step a cell is selected that has an attribute of distance from the starting one less than the current cell. Obviously, in this way the shortest path between a pair of given cells is found [6] . There are several tracks with a minimum numerical path length, both when searching for a path in the vicinity of Moore and von Neumann. The choice of the final path in applications is dictated by other considerations that are outside this algorithm. For example, when tracing printed circuit boards - a minimum of the linear length of the laid conductor.
Pseudo-code
Initialization
Mark start cell d : = 0
Wave propagation
CYCLE
For each loc cell labeled with the number d
mark all adjacent free unlabeled cells with the number d + 1
KC
d : = d + 1
Bye (finish cell is not marked) AND (there is the possibility of wave propagation)
Restoring the path
IF the finish cell is marked
TO
go to the finish cell
CYCLE
among neighboring cells, select a cell marked with a number 1 less than the number in the current cell
go to the selected cell and add it to the path
WHILE the current cell is not a start
RETURN path found
ELSE
RETURN path not found
See also
- Dynamic programming
- PCB trace
- Labyrinth
- List of algorithms
Notes
- ↑ 1 2 The illustration shows the operation of the algorithm if it does not stop after reaching the target cell. At the end of the algorithm, the shortest distance from the starting cell appears in each cell.
- ↑ Moore E. F. The shortest path through a maze // Proceedings of an International Symposium on the Theory of Switching (Cambridge, Massachusetts, 2–5 April 1957) - Harvard University Press , 1959. - Vol. 2. - P. 285–292. - 345 p. - ( Annals of the Computation Laboratory of Harvard University ; Vol. 30)
- ↑ Lee, CY, “An Algorithm for Path Connections and Its Applications”, IRE Transactions on Electronic Computers, vol. EC-10, number 2, pp. 364—365, 1961
- ↑ Cormen et al , Introduction to Algorithms, 3 rd edition, p. 623
- ↑ Mathematics Stack Exchange Origin of the Breadth-First Search algorithm
- ↑ 1 2 Wave Path Algorithm
Literature
- Maxim Mozgovoy. Entertaining programming: a self-instruction manual . - St. Petersburg: Peter, 2004 .-- 208 p. - ISBN 5-94723-853-5 .
- Steven M. Rubin. Computer Aids for VLSI Design . - 1994.
- Wai Kai Chen. The Circuits and Filters Handbook . - 2 nd ed. - 2003 .-- S. 1372-1374. - 2961 s. - ISBN 0-8493-0912-3 .
- Frank Rubin. The Lee path connection algorithm // IEEE Transactions on Computers. - 1974. (unavailable link)
- TH Cormen, CE Leiserson, RL Rivest, C. Stein. Introduction to Algorithms . - 3 rd edition. - The MIT Press, 2009 .-- ISBN 978-0-262-03384-8 .
Links
- Lee Wave Algorithm ( 4 neighbors )
- Lee Wave Algorithm ( 8 neighbors )
- Maze Router: Lee Algorithm (slides)