Second order surface

A second-order surface is the geometrical location of points in three-dimensional space whose rectangular coordinates satisfy an equation of the form

a_{11}x^{2}+a_{22}y^{2}+a_{33}z^{2}+2a_{12}xy+2a_{23}yz+2a_{13}xz+2a_{14}x+2a_{24}y+2a_{34}z+a_{44}=0

{\ displaystyle a_ {11} x ^ {2} + a_ {22} y ^ {2} + a_ {33} z ^ {2} + 2a_ {12} xy + 2a_ {23} yz + 2a_ {13} xz + 2a_ {14} x + 2a_ {24} y + 2a_ {34} z + a_ {44} = 0}

a_ {11} x ^ {2} + a_ {22} y ^ {2} + a_ {33} z ^ {2} + 2a_ {12} xy + 2a_ {23} yz + 2a_ {13} xz + 2a_ { 14} x + 2a_ {24} y + 2a_ {34} z + a_ {44} = 0

in which at least one of the coefficients $a_{11}$ ${\ displaystyle a_ {11}}$ $a_ {11}$ , $a_{22}$ ${\ displaystyle a_ {22}}$ $a _ {{22}}$ , $a_{33}$ ${\ displaystyle a_ {33}}$ $a _ {{33}}$ , $a_{12}$ ${\ displaystyle a_ {12}}$ $a _ {{12}}$ , $a_{23}$ ${\ displaystyle a_ {23}}$ $a _ {{23}}$ , $a_{13}$ ${\ displaystyle a_ {13}}$ $a _ {{13}}$ different from zero.

Second-order surfaces obtained for various values of the parameters of the equation

Types of second-order surfaces

Cylindrical surfaces

Surface $S$ ${\ displaystyle S}$ $S$ called a cylindrical surface with a generatrix ${\vec {l}}$ ${\ displaystyle {\ vec {l}}}$ ${\vec {l}}$ if for any point $M_{0}$ ${\ displaystyle M_ {0}}$ $M_{0}$ of this surface, a straight line passing through this point parallel to ${\vec {l}}$ ${\ displaystyle {\ vec {l}}}$ ${\vec {l}}$ belongs entirely to the surface $S$ ${\ displaystyle S}$ $S$ .

Theorem (on the equation of a cylindrical surface).
If in some Cartesian rectangular coordinate system the surface $S$ ${\ displaystyle S}$ $S$ has an equation $f(x,y)=0$ ${\ displaystyle f (x, y) = 0}$ $f(x,y)=0$ then $S$ ${\ displaystyle S}$ $S$ - a cylindrical surface with a generatrix parallel to the axis $O Z$ ${\ displaystyle OZ}$ $OZ$ .

Equation curve $f(x,y)=0$ ${\ displaystyle f (x, y) = 0}$ $f(x,y)=0$ in the plane $z=0$ ${\ displaystyle z = 0}$ $z=0$ , called the guide cylindrical surface.

If the guide of a cylindrical surface is given by a second-order curve , then such a surface is called a second-order cylindrical surface .


Elliptical cylinder:	Parabolic cylinder:	Hyperbolic cylinder:
${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$ ${\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} + {\ frac {y ^ {2}} {b ^ {2}}} = 1}$ ${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$	$y^{2}=2px$ ${\ displaystyle y ^ {2} = 2px}$ $y^{2}=2px$	${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}\!=1$ ${\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} - {\ frac {y ^ {2}} {b ^ {2}}}!! = 1}$ ${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}\!=1$

A pair of matching lines:	A pair of matching planes:	A pair of intersecting planes:
${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=0$ ${\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} + {\ frac {y ^ {2}} {b ^ {2}}} = 0}$	$y^{2}=0$ ${\ displaystyle y ^ {2} = 0}$	${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}\!=0$ ${\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} - {\ frac {y ^ {2}} {b ^ {2}}}!! = 0}$

Conical surfaces

Conical surface.

Surface $S$ ${\ displaystyle S}$ called a conical surface with a vertex at a point $O$ ${\ displaystyle O}$ if for any point $M_{0}$ ${\ displaystyle M_ {0}}$ this surface is a straight line passing through $M_{0}$ ${\ displaystyle M_ {0}}$ and $O$ ${\ displaystyle O}$ belongs entirely to this surface.

Function $F(x,y,z)$ ${\ displaystyle F (x, y, z)}$ called homogeneous order $m$ ${\ displaystyle m}$ , if a $\forall t\in \mathbb {R} \;\forall x,y,z$ ${\ displaystyle \ forall t \ in \ mathbb {R} \; \ forall x, y, z}$ the following is true: $F(tx,ty,tz)=t^{m}F(x,y,z)$ ${\ displaystyle F (tx, ty, tz) = t ^ {m} F (x, y, z)}$

Theorem (on the equation of a conical surface).
If in some Cartesian rectangular coordinate system the surface $S$ ${\ displaystyle S}$ given by the equation $F(x,y,z)=0$ ${\ displaystyle F (x, y, z) = 0}$ where $F(x,y,z)$ ${\ displaystyle F (x, y, z)}$ Is a homogeneous function then $S$ ${\ displaystyle S}$ - conical surface with a vertex at the origin.

If the surface $S$ ${\ displaystyle S}$ set by function $F(x,y,z)$ ${\ displaystyle F (x, y, z)}$ which is a homogeneous algebraic polynomial of the second order, then $S$ ${\ displaystyle S}$ called a second-order conical surface .

The canonical equation of the second-order cone has the form:

{\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=0

{\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} + {\ frac {y ^ {2}} {b ^ {2}}} - {\ frac {z ^ {2} } {c ^ {2}}} = 0}

Rotation Surfaces

Surface $S$ ${\ displaystyle S}$ called the surface of rotation around the axis $O Z$ ${\ displaystyle OZ}$ if for any point $M_{0}(x_{0},y_{0},z_{0})$ ${\ displaystyle M_ {0} (x_ {0}, y_ {0}, z_ {0})}$ of this surface, a circle passing through this point in the plane $z=z_{0}$ ${\ displaystyle z = z_ {0}}$ centered in $(0,0,z_{0})$ ${\ displaystyle (0,0, z_ {0})}$ and radius $r={\sqrt {x_{0}^{2}+y_{0}^{2}}}$ ${\ displaystyle r = {\ sqrt {x_ {0} ^ {2} + y_ {0} ^ {2}}}}$ belongs entirely to this surface.

Theorem (on the equation of the surface of revolution).
If in some Cartesian rectangular coordinate system the surface $S$ ${\ displaystyle S}$ given by the equation $F(x^{2}+y^{2},z)=0$ ${\ displaystyle F (x ^ {2} + y ^ {2}, z) = 0}$ then $S$ ${\ displaystyle S}$ - surface rotation around the axis $O Z$ ${\ displaystyle OZ}$ .


Ellipsoid :	Single-cavity hyperboloid :	Double Cavity Hyperboloid:	Elliptical Paraboloid :	Hyperbolic paraboloid:
${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}+{\frac {z^{2}}{c^{2}}}=1$ ${\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} + {\ frac {y ^ {2}} {b ^ {2}}} + {\ frac {z ^ {2} } {c ^ {2}}} = 1}$	${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=1$ ${\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} + {\ frac {y ^ {2}} {b ^ {2}}} - {\ frac {z ^ {2} } {c ^ {2}}} = 1}$	${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=-1$ ${\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} + {\ frac {y ^ {2}} {b ^ {2}}} - {\ frac {z ^ {2} } {c ^ {2}}} = - 1}$	${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=2z$ ${\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} + {\ frac {y ^ {2}} {b ^ {2}}} = 2z}$	${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=2z$ ${\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} - {\ frac {y ^ {2}} {b ^ {2}}} = 2z}$

If $a=b\neq 0$ ${\ displaystyle a = b \ neq 0}$ The surfaces listed above are surfaces of revolution.

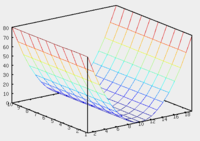
Elliptical Paraboloid

The elliptic paraboloid equation has the form

{\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=2z.

{\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} + {\ frac {y ^ {2}} {b ^ {2}}} = 2z.}

If a $a=b$ ${\ displaystyle a = b}$ , then the elliptical paraboloid is a surface of revolution formed by the rotation of the parabola, the parameter of which $p=a^{2}=b^{2}$ ${\ displaystyle p = a ^ {2} = b ^ {2}}$ , around a vertical axis passing through the vertex and focus of a given parabola.

Intersection of an elliptical paraboloid with a plane $z=z_{0}>0$ ${\ displaystyle z = z_ {0}> 0}$ is an ellipse .

Intersection of an elliptical paraboloid with a plane $x=x_{0}$ ${\ displaystyle x = x_ {0}}$ or $y=y_{0}$ ${\ displaystyle y = y_ {0}}$ is a parabola .

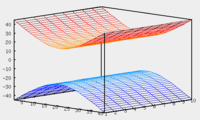
Hyperbolic Paraboloid

The hyperbolic paraboloid equation has the form

{\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=2z.

{\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} - {\ frac {y ^ {2}} {b ^ {2}}} = 2z.}

Intersection of a hyperbolic paraboloid with a plane $z=z_{0}$ ${\ displaystyle z = z_ {0}}$ is a hyperbole .

Intersection of a hyperbolic paraboloid with a plane $x=x_{0}$ ${\ displaystyle x = x_ {0}}$ or $y=y_{0}$ ${\ displaystyle y = y_ {0}}$ is a parabola .

Due to the geometric similarity, a hyperbolic paraboloid is often called a saddle .

Center surfaces

If the center of a second-order surface exists and is unique, then its coordinates $\left(x_{0},\;y_{0}\;z_{0}\right)$ ${\ displaystyle \ left (x_ {0}, \; y_ {0} \; z_ {0} \ right)}$ can be found by solving the system of equations:

${\begin{cases}a_{11}x_{0}+a_{12}y_{0}+a_{13}z_{0}+a_{14}=0\\a_{21}x_{0}+a_{22}y_{0}+a_{23}z_{0}+a_{24}=0\\a_{31}x_{0}+a_{32}y_{0}+a_{33}z_{0}+a_{34}=0\end{cases}}$ ${\ displaystyle {\ begin {cases} a_ {11} x_ {0} + a_ {12} y_ {0} + a_ {13} z_ {0} + a_ {14} = 0 \\ a_ {21} x_ { 0} + a_ {22} y_ {0} + a_ {23} z_ {0} + a_ {24} = 0 \\ a_ {31} x_ {0} + a_ {32} y_ {0} + a_ {33 } z_ {0} + a_ {34} = 0 \ end {cases}}}$

The matrix form of a second-order surface equation

The second-order surface equation can be rewritten in matrix form:

{\begin{pmatrix}x&y&z&1\end{pmatrix}}{\begin{pmatrix}a_{11}&a_{12}&a_{13}&a_{14}\\a_{21}&a_{22}&a_{23}&a_{24}\\a_{31}&a_{32}&a_{33}&a_{34}\\a_{41}&a_{42}&a_{43}&a_{44}\end{pmatrix}}{\begin{pmatrix}x\\y\\z\\1\end{pmatrix}}=0

{\ displaystyle {\ begin {pmatrix} x & y & z & 1 \ end {pmatrix}} {\ begin {pmatrix} a_ {11} & a_ {12} & a_ {13} & a_ {14} \\ a_ {21} & a_ {22} & a_ { 23} & a_ {24} \\ a_ {31} & a_ {32} & a_ {33} & a_ {34} \\ a_ {41} & a_ {42} & a_ {43} & a_ {44} \ end {pmatrix}} {\ begin {pmatrix} x \\ y \\ z \\ 1 \ end {pmatrix}} = 0}

You can also select the quadratic and linear parts from each other:

{\begin{pmatrix}x&y&z\end{pmatrix}}{\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{pmatrix}}{\begin{pmatrix}x\\y\\z\end{pmatrix}}+2{\begin{pmatrix}a_{14}&a_{24}&a_{34}\end{pmatrix}}{\begin{pmatrix}x\\y\\z\end{pmatrix}}+a_{44}=0

{\ displaystyle {\ begin {pmatrix} x & y & z \ end {pmatrix}} {\ begin {pmatrix} a_ {11} & a_ {12} & a_ {13} \\ a_ {21} & a_ {22} & a_ {23} \\ a_ {31} & a_ {32} & a_ {33} \\\ end {pmatrix}} {\ begin {pmatrix} x \\ y \\ z \ end {pmatrix}} + 2 {\ begin {pmatrix} a_ {14 } & a_ {24} & a_ {34} \ end {pmatrix}} {\ begin {pmatrix} x \\ y \\ z \ end {pmatrix}} + a_ {44} = 0}

If designated $A={\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{pmatrix}}\quad b={\begin{pmatrix}a_{14}&a_{24}&a_{34}\end{pmatrix}}\quad X={\begin{pmatrix}x&y&z\end{pmatrix}}^{T}$ ${\ displaystyle A = {\ begin {pmatrix} a_ {11} & a_ {12} & a_ {13} \\ a_ {21} & a_ {22} & a_ {23} \\ a_ {31} & a_ {32} & a_ {33 } \\\ end {pmatrix}} \ quad b = {\ begin {pmatrix} a_ {14} & a_ {24} & a_ {34} \ end {pmatrix}} \ quad X = {\ begin {pmatrix} x & y & z \ end {pmatrix}} ^ {T}}$ , then the equation takes the following form:

X^{T}AX+2bX+a_{44}=0

{\ displaystyle X ^ {T} AX + 2bX + a_ {44} = 0}

Invariants

The values of the following quantities are stored during orthogonal transformations of the basis :

Matrix related $A$ {\ displaystyle A} :
- $I_{1}=\mathrm {tr} \,A$ ${\ displaystyle I_ {1} = \ mathrm {tr} \, A}$
- $I_{2}={M_{A}}_{1,2}^{1,2}+{M_{A}}_{1,3}^{1,3}+{M_{A}}_{2,3}^{2,3}$ {\ displaystyle I_ {2} = {M_ {A}} _ {1,2} ^ {1,2} + {M_ {A}} _ {1,3} ^ {1,3} + {M_ {A }} _ {2,3} ^ {2,3}} where ${M_{A}}_{i,j}^{i,j}$ ${\ displaystyle {M_ {A}} _ {i, j} ^ {i, j}}$ Is the second-order minor of matrix A located in rows and columns with indices i and j.
- $I_{3}=\det A$ ${\ displaystyle I_ {3} = \ det A}$

Associated with the block (expanded) matrix $B$ $=$ $($ $A$ $b$ $b$ $T$ $a$ $44$ $)$ {\ displaystyle B = {\ begin {pmatrix} A & b \\ b ^ {T} & a_ {44} \ end {pmatrix}}} ^[one]
- $K_{2}=\sum _{i=1}^{3}\sum _{j=i+1}^{4}{M_{B}}_{i,j}^{i,j}$ ${\ displaystyle K_ {2} = \ sum _ {i = 1} ^ {3} \ sum _ {j = i + 1} ^ {4} {M_ {B}} _ {i, j} ^ {i, j}}$
- $K_{3}=\sum _{i=1}^{2}\sum _{j=i+1}^{3}\sum _{k=j+1}^{4}{M_{B}}_{i,j,k}^{i,j,k}$ ${\ displaystyle K_ {3} = \ sum _ {i = 1} ^ {2} \ sum _ {j = i + 1} ^ {3} \ sum _ {k = j + 1} ^ {4} {M_ {B}} _ {i, j, k} ^ {i, j, k}}$
- $K_{4}=\det B$ ${\ displaystyle K_ {4} = \ det B}$

Such invariants are also sometimes called semi-invariants or seven-invariants.

With the parallel transfer of the coordinate system $I_{1},I_{2},I_{3},K_{4}$ ${\ displaystyle I_ {1}, I_ {2}, I_ {3}, K_ {4}}$ remain unchanged. Wherein:

$K_{3}$ ${\ displaystyle K_ {3}}$ remains unchanged only if $I_{2}=I_{3}=K_{4}=0$ ${\ displaystyle I_ {2} = I_ {3} = K_ {4} = 0}$
$K_{2}$ ${\ displaystyle K_ {2}}$ remains unchanged only if $I_{2}=I_{3}=K_{4}=K_{3}=0$ ${\ displaystyle I_ {2} = I_ {3} = K_ {4} = K_ {3} = 0}$

Classification of second-order surfaces with respect to the values of invariants


Surface	The equation	Invariants
Ellipsoid	${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}+{\frac {z^{2}}{c^{2}}}=1$ ${\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} + {\ frac {y ^ {2}} {b ^ {2}}} + {\ frac {z ^ {2} } {c ^ {2}}} = 1}$	$I_{3}\neq 0$ ${\ displaystyle I_ {3} \ neq 0}$	$I_{2}>0,\quad I_{1}I_{3}>0$ ${\ displaystyle I_ {2}> 0, \ quad I_ {1} I_ {3}> 0}$	$I_{4}<0$ ${\ displaystyle I_ {4} <0}$
Imaginary ellipsoid	${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}+{\frac {z^{2}}{c^{2}}}=-1$ ${\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} + {\ frac {y ^ {2}} {b ^ {2}}} + {\ frac {z ^ {2} } {c ^ {2}}} = - 1}$			$I_{4}>0$ ${\ displaystyle I_ {4}> 0}$
Point	${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}+z^{2}=0$ ${\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} + {\ frac {y ^ {2}} {b ^ {2}}} + z ^ {2} = 0}$			$I_{4}=0$ ${\ displaystyle I_ {4} = 0}$
Single Cavity Hyperboloid	${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=1$ ${\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} + {\ frac {y ^ {2}} {b ^ {2}}} - {\ frac {z ^ {2} } {c ^ {2}}} = 1}$		$I_{2}=0$ ${\ displaystyle I_ {2} = 0}$ or $I_{1}I_{3}\leq 0$ ${\ displaystyle I_ {1} I_ {3} \ leq 0}$	$I_{4}>0$ ${\ displaystyle I_ {4}> 0}$
Double Cavity Hyperboloid	${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=-1$ ${\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} + {\ frac {y ^ {2}} {b ^ {2}}} - {\ frac {z ^ {2} } {c ^ {2}}} = - 1}$			$I_{4}<0$ ${\ displaystyle I_ {4} <0}$
Cone	${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-2z^{2}=0$ ${\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} + {\ frac {y ^ {2}} {b ^ {2}}} - 2z ^ {2} = 0}$			$I_{4}=0$ ${\ displaystyle I_ {4} = 0}$
Elliptical paraboloid	${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-2z=0$ ${\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} + {\ frac {y ^ {2}} {b ^ {2}}} - 2z = 0}$	$I_{3}=0$ ${\ displaystyle I_ {3} = 0}$	$I_{4}\neq 0$ ${\ displaystyle I_ {4} \ neq 0}$	$I_{4}<0$ ${\ displaystyle I_ {4} <0}$
Hyperbolic paraboloid	${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}-2z=0$ ${\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} - {\ frac {y ^ {2}} {b ^ {2}}} - 2z = 0}$		$I_{4}\neq 0$ ${\ displaystyle I_ {4} \ neq 0}$	$I_{4}>0$ ${\ displaystyle I_ {4}> 0}$
Elliptical cylinder	${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$ ${\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} + {\ frac {y ^ {2}} {b ^ {2}}} = 1}$		$I_{4}=0$ ${\ displaystyle I_ {4} = 0}$	$I_{2}>0$ ${\ displaystyle I_ {2}> 0}$	$I_{1}K_{2}<0$ ${\ displaystyle I_ {1} K_ {2} <0}$
Imaginary elliptical cylinder	${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=-1$ ${\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} + {\ frac {y ^ {2}} {b ^ {2}}} = - 1}$				$I_{1}K_{2}>0$ ${\ displaystyle I_ {1} K_ {2}> 0}$
Straight (pair of imaginary intersecting planes)	${\frac {x^{2}}{a^{2}}}+y^{2}=0$ ${\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} + y ^ {2} = 0}$				$K_{2}=0$ ${\ displaystyle K_ {2} = 0}$
Hyperbolic cylinder	${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1$ ${\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} - {\ frac {y ^ {2}} {b ^ {2}}} = 1}$			$I_{2}<0$ ${\ displaystyle I_ {2} <0}$	$K_{2}\neq 0$ ${\ displaystyle K_ {2} \ neq 0}$
Pair of intersecting planes	${\frac {x^{2}}{a^{2}}}-y^{2}=0$ ${\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} - y ^ {2} = 0}$			$I_{2}<0$ ${\ displaystyle I_ {2} <0}$	$K_{2}=0$ ${\ displaystyle K_ {2} = 0}$
Parabolic cylinder	$y^{2}=2px$ ${\ displaystyle y ^ {2} = 2px}$			$I_{2}=0$ ${\ displaystyle I_ {2} = 0}$	$K_{2}\neq 0$ ${\ displaystyle K_ {2} \ neq 0}$
Pair of parallel planes	$x^{2}-d^{2}=0$ ${\ displaystyle x ^ {2} -d ^ {2} = 0}$				$K_{2}=0$ ${\ displaystyle K_ {2} = 0}$	$K_{1}<0$ ${\ displaystyle K_ {1} <0}$
A pair of imaginary parallel planes	$x^{2}+d^{2}=0$ ${\ displaystyle x ^ {2} + d ^ {2} = 0}$					$K_{1}>0$ ${\ displaystyle K_ {1}> 0}$
Plane	$x^{2}=0$ ${\ displaystyle x ^ {2} = 0}$					$K_{1}=0$ ${\ displaystyle K_ {1} = 0}$

Notes

↑ Alexandrov P.S., Chapter XIX. General theory of second-order surfaces. // Lectures on analytic geometry. - Science, 1968 .-- S. 504-506. - 911 p.

Literature

V.A. Ilyin, G. D. Kim. Linear algebra and analytic geometry. - M .: Prospect, 2012 .-- 400 p.
V.A. Ilyin, E.G. Poznyak. Analytic geometry. - M .: FIZMATLIT, 2002 .-- 240 p.
P.S. Alexandrov. Course of analytic geometry and linear algebra. - M .: FIZMATLIT, 1979. - 511 p.
Shawl . A historical review of the origin and development of geometric methods . Ch. 5, § 46-54. M., 1883.

Second order surface