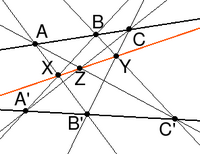
Papp's Theorem

Papp's theorem is a classical theorem of projective geometry . It is formulated as follows:

Let A , B , C be three points on one line, A ' , B' , C ' be three points on another line. Let three lines AB ' , BC' , CA ' intersect three lines A'B , B'C , C'A , respectively, at points X , Y , Z. Then the points X , Y , Z lie on the same line.

It is easy to see that the dual formulation to Papp's theorem is only a reformulation of the theorem itself:

Let the lines $a_{1},a_{2},a_{3}$ ${\ displaystyle a_ {1}, a_ {2}, a_ {3}}$ $a_ {1}, a_ {2}, a_ {3}$ pass through point A, $a_{1}',a_{2}',a_{3}'$ ${\ displaystyle a_ {1} ', a_ {2}', a_ {3} '}$ $a_ {1} ', a_ {2}', a_ {3} '$ pass through point A '. $a_{1}$ ${\ displaystyle a_ {1}}$ $a_ {1}$ crosses $a_{2}'$ ${\ displaystyle a_ {2} '}$ $a_ {2} '$ and $a_{3}'$ ${\ displaystyle a_ {3} '}$ $a_ {3} '$ at points B and C, $a_{2}'$ ${\ displaystyle a_ {2} '}$ $a_ {2} '$ crosses $a_{1}'$ ${\ displaystyle a_ {1} '}$ $a_ {1} '$ and $a_{3}'$ ${\ displaystyle a_ {3} '}$ $a_ {3} '$ at points C 'and Z, $a_{3}$ ${\ displaystyle a_ {3}}$ $a_ {3}$ crosses $a_{1}'$ ${\ displaystyle a_ {1} '}$ $a_ {1} '$ and $a_{2}'$ ${\ displaystyle a_ {2} '}$ $a_ {2} '$ at points B 'and X. Then the lines BC', B'C and XZ intersect at one point (point Y in the drawing) or parallel.

Pappa's theorem is a degenerate case in Pascal's theorem : if, in Pascal's theorem, the hexagon inscribed in a conic is replaced by an inscribed in a pair of intersecting lines, then it becomes equivalent to Pappa's theorem. Pascal himself considered a pair of lines to be a conic section (that is, he considered Papp's theorem a special case of his theorem).

Content

History

The statement and proof of this theorem are contained in the "Mathematical Collection" of Papp of Alexandria (beginning of the 4th century A.D.). In modern times, the theorem was published by the publisher and commentator on Papp Federico Commandino in 1566 .

Evidence

Points X, Y, Z lie on one line

Proof by removing points to infinity

Let the point $O$ ${\ displaystyle O}$ is the intersection point of the lines on which the points lie $A$ ${\ displaystyle A}$ , $B$ ${\ displaystyle B}$ , $C$ ${\ displaystyle C}$ and $A^{'}$ ${\ displaystyle A '}$ , $B^{'}$ ${\ displaystyle B '}$ , $C^{'}$ ${\ displaystyle C '}$ .

Consider the intersection of lines:

$AB'\bigcap A'B=X$ ${\ displaystyle AB '\ bigcap A'B = X}$

$AC'\bigcap A'C=Y$ ${\ displaystyle AC '\ bigcap A'C = Y}$

$CB'\bigcap C'B=Z$ ${\ displaystyle CB '\ bigcap C'B = Z}$

Now apply the projective mapping that translates the line $X Y$ ${\ displaystyle XY}$ to infinity. Then $AC'||A'C$ ${\ displaystyle AC '|| A'C}$ .

Because $X=\infty$ ${\ displaystyle X = \ infty}$ : $AB'||A'B$ ${\ displaystyle AB '|| A'B}$ . Now it is necessary to prove that $BC'||B'C$ ${\ displaystyle BC '|| B'C}$ .

Consider these triangles.

$\bigtriangleup OAC'\sim \ \bigtriangleup OCA'\Rightarrow {\frac {OC}{OA'}}={\frac {OA}{OC'}}\Rightarrow OA\cdot OA'=OC\cdot OC'$ ${\ displaystyle \ bigtriangleup OAC '\ sim \ \ bigtriangleup OCA' \ Rightarrow {\ frac {OC} {OA '}} = {\ frac {OA} {OC'}} \ Rightarrow OA \ cdot OA '= OC \ cdot OC '}$

$\bigtriangleup OAB'\sim \ \bigtriangleup OBA'\Rightarrow {\frac {OB}{OA'}}={\frac {OA}{OB'}}\Rightarrow OA\cdot OA'=OB\cdot OB'$ ${\ displaystyle \ bigtriangleup OAB '\ sim \ \ bigtriangleup OBA' \ Rightarrow {\ frac {OB} {OA '}} = {\ frac {OA} {OB'}} \ Rightarrow OA \ cdot OA '= OB \ cdot OB '}$

It follows that ${\frac {OB}{OC}}={\frac {OB'}{OC'}}\Rightarrow \bigtriangleup OCB'\sim \bigtriangleup OBC'$ ${\ displaystyle {\ frac {OB} {OC}} = {\ frac {OB '} {OC'}} \ Rightarrow \ bigtriangleup OCB '\ sim \ bigtriangleup OBC'}$ (by the second sign of the similarity of triangles ) $\Rightarrow BC'||B'C$ ${\ displaystyle \ Rightarrow BC '|| B'C}$ .

Q.E.D.

Proof through Menelaus theorem

Applying to Triangles $\bigtriangleup AXB$ ${\ displaystyle \ bigtriangleup AXB}$ , $\bigtriangleup AYC$ ${\ displaystyle \ bigtriangleup AYC}$ and $\bigtriangleup BZC$ ${\ displaystyle \ bigtriangleup BZC}$ Menelaus theorem , one can also prove this statement.

Links

R. Courant, G. Robbins, What is Mathematics? Chapter IV, § 5.3.