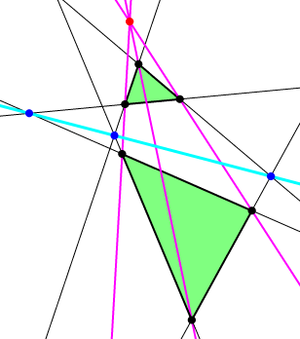
Desargues theorem is one of the main theorems of projective geometry . It is formulated as follows:
If two triangles are located on the plane in such a way that the lines connecting the corresponding vertices of the triangles pass through one point, then the three points at which the extensions of three pairs of the corresponding sides of the triangles intersect lie on one straight line. |
The converse is also true:
If two triangles are located on the plane in such a way that the three points at which the extensions of the three pairs of the corresponding sides of the triangles intersect lie on one straight line, then the lines connecting the corresponding vertices of the triangles pass through one point. |
These two theorems are dual in relation to each other, and are sometimes combined into a single theorem, which is formulated as follows: "Two triangles have a center of perspective [1] if and only if they have a perspective axis [2] ."
Content
About evidence
- One of the most common evidence is based on the transition to three-dimensional space - it is enough to imagine both triangles with two sections of a trihedral pyramid. The whole picture is considered as a projection onto the plane of the spatial structure.
- Another proof is the application of a projective transformation, which takes two of the intersections of the extensions of the sides to an ideal line. After this, it remains to prove the parallelism of the third pair of parties. The latter is easy to see from the likeness of triangles.
- Another proof is the threefold use of Menelaus' theorem .
Variations and generalizations
Poncelet based on her his elegant theory of homological figures . He called the two triangles referred to in the Desargues theorem homological, the intersection point of the lines connecting their vertices in pairs, the center of homology, and the line on which their sides intersect in pairs, the axis of homology.
Poncelet gave the following theorem for geometry in space, as corresponding to the Desargues theorem on the plane:
If two tetrahedra have vertices lying in pairs on four lines converging at one point, then the planes of opposite faces intersect along four lines that are in the same plane. |
This theorem can be generalized even further as follows:
When the vertices of two tetrahedra are placed in pairs on four lines belonging to the same group of generators of a hyperboloid with one cavity, then their faces intersect in four lines that belong to the generators of another hyperboloid. |
Desargues Configuration
Points and lines in Desargues theorem form the so-called Desargues configuration . Here 3 lines pass through each of 10 points and 3 points lie on each of 10 lines. Moreover, any of the 10 points can be taken as “the top of the trihedral pyramid” (“Desargues point”) in the above proof. Any line can be taken as a "desargue line." The fixation of the separation point or the separation line fully determines the entire configuration.
Desargues theorem and axiomatics of projective geometry
In constructing the projective geometry of the plane, without going into three-dimensional space, Desargues' theorem is not derived from the basic axioms of the projective plane . This means that it is possible to construct a projective plane where Desargues theorem is not true. For example, a Cayley plane is a projective plane over a Cayley algebra is not desargue, see also non-marginal geometry .
When constructing a desargue projective plane, the assertion of Desargues theorem is added to the system of axioms of the projective plane as another axiom.
History
Desargues theorem was discovered by the French geometer Desargues : it, together with two others, of which one is its inverse, was placed at the end of the work Traité de perspective , compiled by Boss according to the principles and method of Desargues and appeared in 1636. In this essay, it was noted that this statement is obvious when the triangles are in two different planes; consideration of the case when they lie in the same plane provides one of the first examples of the use of Menelaus theorem for new geometers. Desargues theorem became famous at the beginning of the XIX century due to its use in the works of Brianchon and Poncelet .
See also
- Papp's Theorem
Notes
- ↑ That is, the point at which three lines intersect through pairs of corresponding vertices intersect.
- ↑ That is, the straight line on which the straight lines containing the corresponding sides intersect.
Links
- Shawl, Michelle . A historical review of the origin and development of geometric methods . T. 1, § 28.M., 1883.
- Coxeter G. S. M. , Greitzer S. P. New Encounters with Geometry . - M .: Nauka , 1978. - T. 14. - ( Library of the mathematical circle ).
- Ponarin I.P. Elementary geometry. In 2 vols .-- M .: MCCNMO , 2004 .-- S. 74-76. - ISBN 5-94057-170-0 .