Holomorphic function

The holomorphic function performs conformal mapping , transforming the orthogonal grid to the same orthogonal (where the complex derivative does not vanish).

A holomorphic function , sometimes called a regular function, is a function of a complex variable defined on an open subset of the complex plane $\mathbb {C}$ ${\ displaystyle \ mathbb {C}}$ $\ mathbb {C}$ and complex differentiable at each point.

Unlike the real case, this condition means that the function is infinitely differentiable and can be represented by the Taylor series converging to it.

Holomorphic functions are also sometimes called analytic , although the second concept is much broader, since an analytic function does not have to be defined on the set of complex numbers. The fact that for complex-valued functions of a complex variable the sets of holomorphic and analytic functions coincide is a nontrivial and very remarkable result of complex analysis.

Definition

Let be $U$ ${\ displaystyle U}$ $U$ Is an open subset of $\mathbb {C}$ ${\ displaystyle \ mathbb {C}}$ $\mathbb {C}$ and $f:U\to \mathbb {C}$ ${\ displaystyle f: U \ to \ mathbb {C}}$ $f:U\to {\mathbb {C}}$ Is a complex-valued function on $U$ ${\ displaystyle U}$ $U$ .

Function $f$ {\ displaystyle f} called complex differentiable at $z$ $0$ $\in$ $U$ {\ displaystyle z_ {0} \ in U} if there is a limit
$f'(z_{0})=\lim _{z\to z_{0}}{\frac {f(z)-f(z_{0})}{z-z_{0}}}.$ ${\ displaystyle f '(z_ {0}) = \ lim _ {z \ to z_ {0}} {\ frac {f (z) -f (z_ {0})} {z-z_ {0}}} .}$ $f'(z_{0})=\lim _{{z\to z_{0}}}{\frac {f(z)-f(z_{0})}{z-z_{0}}}.$
- In this expression, the limit is taken over all sequences of complex numbers converging to $z_{0}$ ${\ displaystyle z_ {0}}$ $z_{0}$ , for all such sequences, the expression must converge to the same number $f'(z_{0})$ ${\ displaystyle f '(z_ {0})}$ $f'(z_{0})$ . Complex differentiation is in many ways similar to real : it is linear and satisfies the Leibniz identity .
Function $f$ ${\ displaystyle f}$ $f$ called holomorphic in $U$ ${\ displaystyle U}$ $U$ if it is complex differentiable at each point $U$ ${\ displaystyle U}$ $U$ .
Function $f$ ${\ displaystyle f}$ $f$ called holomorphic in $z_{0}\in U$ ${\ displaystyle z_ {0} \ in U}$ $z_{0}\in U$ if it is complex differentiable in some neighborhood $z_{0}$ ${\ displaystyle z_ {0}}$ $z_{0}$ .

Another definition

The definition of a holomorphic function can be given a slightly different form if we use the operators ${\frac {\partial }{\partial z}}$ ${\ displaystyle {\ frac {\ partial} {\ partial z}}}$ and ${\frac {\partial }{\partial {\bar {z}}}}$ ${\ displaystyle {\ frac {\ partial} {\ partial {\ bar {z}}}}}$ defined by the rule

{\frac {\partial }{\partial z}}={1 \over 2}\left({\frac {\partial }{\partial x}}-i{\frac {\partial }{\partial y}}\right),

{\ displaystyle {\ frac {\ partial} {\ partial z}} = {1 \ over 2} \ left ({\ frac {\ partial} {\ partial x}} - i {\ frac {\ partial} {\ partial y}} \ right),}

{\frac {\partial }{\partial {\bar {z}}}}={1 \over 2}\left({\frac {\partial }{\partial x}}+i{\frac {\partial }{\partial y}}\right),

{\ displaystyle {\ frac {\ partial} {\ partial {\ bar {z}}}} = {1 \ over 2} \ left ({\ frac {\ partial} {\ partial x}} + i {\ frac {\ partial} {\ partial y}} \ right),}

Where $z=x+iy$ ${\ displaystyle z = x + iy}$ . Then the function $f$ ${\ displaystyle f}$ is called holomorphic if

{\frac {\partial f}{\partial {\bar {z}}}}=0,

{\ displaystyle {\ frac {\ partial f} {\ partial {\ bar {z}}}} = 0,}

which is equivalent to the Cauchy-Riemann conditions .

Related Definitions

An entire function is a function holomorphic on the entire complex plane.
Meromorphic function - a function holomorphic in a domain $\Omega /\{{z_{i}},\;i\in I\}$ ${\ displaystyle \ Omega / \ {{z_ {i}}, \; i \ in I \}}$ and having at all its special points $z_{i}$ ${\ displaystyle z_ {i}}$ the pole .
Function $f$ ${\ displaystyle f}$ is called holomorphic on a compact $K$ ${\ displaystyle K}$ if there is an open set $D$ ${\ displaystyle D}$ containing $K$ ${\ displaystyle K}$ such that $f$ ${\ displaystyle f}$ holomorphic in $D$ ${\ displaystyle D}$ .

Properties

Complex function $u+iv=f(x+iy)$ ${\ displaystyle u + iv = f (x + iy)}$ is holomorphic if and only if the Cauchy - Riemann conditions are satisfied
${\frac {\partial u}{\partial x}}={\frac {\partial v}{\partial y}};\quad {\frac {\partial u}{\partial y}}=-{\frac {\partial v}{\partial x}}$ ${\ displaystyle {\ frac {\ partial u} {\ partial x}} = {\ frac {\ partial v} {\ partial y}}; \ quad {\ frac {\ partial u} {\ partial y}} = - {\ frac {\ partial v} {\ partial x}}}$

and private derivatives

{\frac {\partial u}{\partial x}},\;{\frac {\partial u}{\partial y}},\;{\frac {\partial v}{\partial x}},\;{\frac {\partial v}{\partial y}}

{\ displaystyle {\ frac {\ partial u} {\ partial x}}, \; {\ frac {\ partial u} {\ partial y}}, \; {\ frac {\ partial v} {\ partial x} }, \; {\ frac {\ partial v} {\ partial y}}}

continuous.

The sum and product of holomorphic functions is a holomorphic function, which follows from the linearity of differentiation and the fulfillment of the Leibniz rule. The quotient of holomorphic functions is also holomorphic at all points where the denominator does not turn to 0.
The derivative of a holomorphic function is again holomorphic; therefore, holomorphic functions are infinitely differentiable in their domain of definition.
Holomorphic functions are analytic , that is, they can be represented as a Taylor series converging in some neighborhood of each point. Thus, for complex functions of a complex variable, the sets of holomorphic and analytic functions coincide.
From any holomorphic function, one can distinguish its real and imaginary parts, each of which will be a solution of the Laplace equation in $\mathbb {R} ^{2}$ ${\ displaystyle \ mathbb {R} ^ {2}}$ . That is, if $f(x+iy)=u(x,\;y)+iv(x,\;y)$ ${\ displaystyle f (x + iy) = u (x, \; y) + iv (x, \; y)}$ Is a holomorphic function then $u$ ${\ displaystyle u}$ and $v$ ${\ displaystyle v}$ - harmonic functions.
If the absolute value of a holomorphic function reaches a local maximum at the internal point of its domain of definition, then the function is constant (it is assumed that the domain of definition is connected). It follows that the maximum (and minimum, if it is not equal to zero) of the absolute value of the holomorphic function can be achieved only at the boundary of the region.
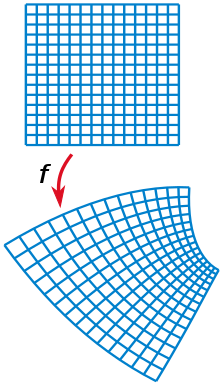
In a region where the first derivative of a holomorphic function does not vanish and the function is univalent , it carries out conformal mapping .
The Cauchy integral formula relates the value of a function at the internal point of a region to its values on the boundary of this region.
From an algebraic point of view, the set of holomorphic functions on an open set of functions is a commutative ring and a complex linear space . This is a locally convex topological vector space with a seminorm equal to a supremum on compact subsets.
According to the Weierstrass theorem , if a series of holomorphic functions in the domain $D$ ${\ displaystyle D}$ converges uniformly on any compact in $D,$ ${\ displaystyle D,}$ then its sum is also holomorphic, and its derivative is the limit of the derivatives of partial sums of the series ^[1] .

History

The term "holomorphic function" was introduced by two students of Cauchy , Brio ( 1817 - 1882 ) and Bouquet ( 1819 - 1895 ), and comes from the Greek words őλoς ( holos ), which means "whole", and μoρφń ( morphe ) - form, image . ^[2]

Today, many mathematicians prefer the term "holomorphic function" instead of "analytic function", since the second concept is more general. In addition, one of the important results of complex analysis is that any holomorphic function is analytic, which is not obvious from the definition. The term “analytical” is usually used for more general functions that are not necessarily defined on the complex plane.

Variations and generalizations

Multidimensional Case

There is also a definition of holomorphy of functions of many complex variables

f\colon \mathbb {C} ^{n}\to \mathbb {C} .

{\ displaystyle f \ colon \ mathbb {C} ^ {n} \ to \ mathbb {C}.}

For definition, concepts are used $\mathbb {C}$ ${\ displaystyle \ mathbb {C}}$ -differentiability and $\mathbb {C}$ ${\ displaystyle \ mathbb {C}}$ -linearity of such functions

C-linearity

Function $f$ ${\ displaystyle f}$ called $\mathbb {C}$ ${\ displaystyle \ mathbb {C}}$ -linear if the conditions are satisfied:

$f(z'+z'')=f(z')+f(z''),\quad z',\;z''\in \mathbb {C} ^{n}$ ${\ displaystyle f (z '+ z' ') = f (z') + f (z ''), \ quad z ', \; z' '\ in \ mathbb {C} ^ {n}}$ .
$f(\lambda z)=\lambda f(z),\quad z\in \mathbb {C} ^{n},\quad \lambda \in \mathbb {C}$ ${\ displaystyle f (\ lambda z) = \ lambda f (z), \ quad z \ in \ mathbb {C} ^ {n}, \ quad \ lambda \ in \ mathbb {C}}$

(for $\mathbb {R}$ ${\ displaystyle \ mathbb {R}}$ -linear functions $\lambda \in \mathbb {R}$ ${\ displaystyle \ lambda \ in \ mathbb {R}}$ )

For any $\mathbb {R}$ ${\ displaystyle \ mathbb {R}}$ -linear function $f$ ${\ displaystyle f}$ there are sequences $\{a_{n}\},\;\{b_{n}\}\subset \mathbb {C}$ ${\ displaystyle \ {a_ {n} \}, \; \ {b_ {n} \} \ subset \ mathbb {C}}$ such that $f=\sum _{i=1}^{n}(a_{i}z_{i}+b_{i}{\bar {z}}_{i})$ ${\ displaystyle f = \ sum _ {i = 1} ^ {n} (a_ {i} z_ {i} + b_ {i} {\ bar {z}} _ {i})}$ .
For any $\mathbb {C}$ ${\ displaystyle \ mathbb {C}}$ -linear function $f$ ${\ displaystyle f}$ there is a sequence $\{a_{n}\}\subset \mathbb {C}$ ${\ displaystyle \ {a_ {n} \} \ subset \ mathbb {C}}$ such that $f=\sum _{i=1}^{n}a_{i}z_{i}$ ${\ displaystyle f = \ sum _ {i = 1} ^ {n} a_ {i} z_ {i}}$ .

C-differentiability

Function $f$ ${\ displaystyle f}$ called $\mathbb {C}$ ${\ displaystyle \ mathbb {C}}$ differentiable at a point $z\in \mathbb {C} ^{n}$ ${\ displaystyle z \ in \ mathbb {C} ^ {n}}$ if functions exist $l$ ${\ displaystyle l}$ and $o$ ${\ displaystyle o}$ such that in a neighborhood of the point $z$ ${\ displaystyle z}$

f(z+h)=f(z)+l(h)+o(h),\quad \lim _{h\to 0}{\frac {o(h)}{h}}=0,

{\ displaystyle f (z + h) = f (z) + l (h) + o (h), \ quad \ lim _ {h \ to 0} {\ frac {o (h)} {h}} = 0,}

Where $l$ ${\ displaystyle l}$ - $\mathbb {C}$ ${\ displaystyle \ mathbb {C}}$ -linear (for $\mathbb {R}$ ${\ displaystyle \ mathbb {R}}$ -differentiability - $\mathbb {R}$ ${\ displaystyle \ mathbb {R}}$ -linear) function.

Holomorphy

Function $f$ ${\ displaystyle f}$ is called holomorphic in the region $D,$ ${\ displaystyle D,}$ If she $\mathbb {C}$ ${\ displaystyle \ mathbb {C}}$ -differentiable in a neighborhood of each point of this region.

Quasianalyticity

Links

↑ A.V. Domrin, A.G. Sergeev. Lectures on complex analysis. The first half of the year. - M .: Steklov Mathematical Institute, 2004 .-- S. 79. - ISBN 5-98419-007-9 .
↑ Markushevich AI, Silverman, Richard A. (ed.) Theory of functions of a Complex Variable. - M .: American Mathematical Society , 2nd ed. - ISBN 0-8218-3780-X , [1] .

Literature

Holomorphic function // Brockhaus and Efron Encyclopedic Dictionary : 86 volumes (82 volumes and 4 additional). - SPb. , 1890-1907.
Shabat B.V. Introduction to complex analysis. - M .: Science , 1969 . - 577 p.
Titchmarsh E. Theory of functions: Per. from English - 2nd ed., Revised. - M .: Science , 1980 . - 464 p.
Privalov I. I. Introduction to the theory of functions of a complex variable: A manual for higher education. - M.-L.: State Publishing House, 1927 . - 316 p.
Evgrafov M.A. Analytical functions. - 2nd ed., Revised. and add. - M .: Science , 1968 . - 472 p.