Hyperbola (math)

Hyperbole and its tricks

Cross sections of cones by plane (with eccentricity greater than unity)

Hyperbola ( dr. Greek ὑπερβολή , from ὑπερ - “top” + βαλειν - “throw”) - the geometric place of points M of the Euclidean plane , for which the absolute value of the difference in distances from M to two selected points $F_{1}$ ${\ displaystyle F_ {1}}$ $F_ {1}$ and $F_{2}$ ${\ displaystyle F_ {2}}$ $F_ {2}$ (called magic tricks ) constantly. More precisely,

{\bigl |}|F_{1}M|-|F_{2}M|{\bigr |}=2a,

{\ displaystyle {\ bigl |} | F_ {1} M | - | F_ {2} M | {\ bigr |} = 2a,}

{\ bigl |} | F_ {1} M | - | F_ {2} M | {\ bigr |} = 2a,

moreover

|F_{1}F_{2}|>2a>0.

{\ displaystyle | F_ {1} F_ {2} |> 2a> 0.}

| F_ {1} F_ {2} |> 2a> 0.

Along with an ellipse and a parabola , a hyperbola is a conic section and a quadric . A hyperbola can be defined as a conical section with an eccentricity greater than unity.

History

The term “hyperbole” ( Greek ὑπερβολή - excess) was introduced by Apollonius of Perga (c. 262 BC - c. 190 BC ), since the problem of constructing a hyperbola point reduces to the problem of applying with excess .

Definitions

Hyperbole can be defined in several ways.

Conical section

Three main conical sections

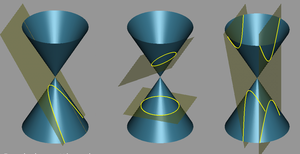
A hyperbola can be defined as a set of points formed as a result of the section of a circular cone by a plane cutting off both parts of the cone. Other results of a section of a cone by a plane are a parabola , an ellipse , as well as degenerate cases such as intersecting and coincident lines and a point that occur when the secant plane passes through the vertex of the cone. In particular, intersecting straight lines can be considered a degenerate hyperbola, coinciding with its asymptotes.

How a geometric place of dots

Through Magic

A hyperbola can be defined as the geometrical location of points , the absolute value of the difference in the distances from which to two given points, called foci, is constant.

For comparison: the curve of a constant sum of distances from any point to foci is an ellipse , a constant ratio is the circle of Apollonius , a constant product is the Cassini oval .

Via Directrix and Focus

The geometric location of the points for which the ratio of the distance to the focus and to a given line, called the directrix , is constant and greater than unity, is called a hyperbola. Preset constant $\varepsilon >1$ ${\ displaystyle \ varepsilon> 1}$ called the eccentricity of the hyperbola.

Related Definitions

The asymptotes of the hyperbola (red curves) shown by the blue dotted line intersect in the center of the hyperbola, C. Two foci of hyperbola are designated as F ₁ and F ₂ . The directors of the hyperbola are indicated by lines of double thickness and are indicated by D ₁ and D ₂ . The eccentricity ε is equal to the ratio of the distances of the point P on the hyperbole to the focus and to the corresponding directrix (shown in green). The vertices of the hyperbola are designated as ± a . Hyperbola parameters mean the following:

a is the distance from the center C to each of the vertices
b - the length of the perpendicular to the abscissa axis, restored from each of the vertices to the intersection with the asymptote
c is the distance from the center of C to any of the foci, F ₁ and F ₂ ,
θ is the angle formed by each of the asymptotes and the axis drawn between the vertices

A hyperbola consists of two separate curves called branches .
The points nearest to each other of two branches of a hyperbola are called vertices .
The shortest distance between two branches of a hyperbola is called the major axis of the hyperbola.
The middle of the major axis is called the center of the hyperbola.
The distance from the center of the hyperbola to one of the peaks is called the semi-major axis of the hyperbola.
- Usually denoted by a .
The distance from the center of the hyperbola to one of the tricks is called the focal distance .
- Commonly denoted by c .
Both focuses of the hyperbola lie on the continuation of the major axis at the same distance from the center of the hyperbola. A straight line containing the major axis of the hyperbola is called the real , or transverse , axis of the hyperbola.
The straight line, perpendicular to the real axis and passing through its center, is called the imaginary , or conjugate , axis of the hyperbola.
The segment between the focus of the hyperbola and the hyperbola, perpendicular to its real axis, is called the focal parameter .
The distance from the focus to the asymptote of the hyperbola is called the impact parameter .
- Usually denoted by b .
In problems associated with the motion of bodies along hyperbolic trajectories, the distance from the focus to the nearest vertex of the hyperbola is called the pericentric distance
- Usually indicated $r_{p}$ ${\ displaystyle r_ {p}}$ .

Relationships

For the characteristics of the hyperbola defined above, the following relations exist

$c^{2}=a^{2}+b^{2}$ ${\ displaystyle c ^ {2} = a ^ {2} + b ^ {2}}$ .
$\varepsilon =c/a$ ${\ displaystyle \ varepsilon = c / a}$ .
$b^{2}=a^{2}\left(\varepsilon ^{2}-1\right)$ ${\ displaystyle b ^ {2} = a ^ {2} \ left (\ varepsilon ^ {2} -1 \ right)}$ .
$r_{p}=a\left(\varepsilon -1\right)$ ${\ displaystyle r_ {p} = a \ left (\ varepsilon -1 \ right)}$ .
$a={\frac {p}{\varepsilon ^{2}-1}}$ ${\ displaystyle a = {\ frac {p} {\ varepsilon ^ {2} -1}}}$ .
$b={\frac {p}{\sqrt {\varepsilon ^{2}-1}}}$ ${\ displaystyle b = {\ frac {p} {\ sqrt {\ varepsilon ^ {2} -1}}}}$ .
$c={\frac {p\varepsilon }{\varepsilon ^{2}-1}}$ ${\ displaystyle c = {\ frac {p \ varepsilon} {\ varepsilon ^ {2} -1}}}$ .
$p={\frac {b^{2}}{a}}$ ${\ displaystyle p = {\ frac {b ^ {2}} {a}}}$ .

Equivalent Hyperbole

Equidistant hyperbole

Hyperbola, in which $a=b$ ${\ displaystyle a = b}$ are called equal - sided , or equilateral . An equilateral hyperbole in some rectangular coordinate system is described by the equation

xy=a^{2}/2,

{\ displaystyle xy = a ^ {2} / 2,}

the foci of the hyperbola are located at points ( a, a ) and ( −a, −a ). An equilateral hyperbole is a graph of inverse proportionality given by the formula:

y={\frac {k}{x}},k\neq 0.

{\ displaystyle y = {\ frac {k} {x}}, k \ neq 0.}

The eccentricity of such a hyperbola is ${\sqrt {2}}$ ${\ displaystyle {\ sqrt {2}}}$ .

Equations

Cartesian coordinates

The hyperbola is given by an equation of the second degree in the Cartesian coordinates ( x , y ) on the plane:

A_{xx}x^{2}+2A_{xy}xy+A_{yy}y^{2}+2B_{x}x+2B_{y}y+C\,=\,0

{\ displaystyle A_ {xx} x ^ {2} + 2A_ {xy} xy + A_ {yy} y ^ {2} + 2B_ {x} x + 2B_ {y} y + C \, = \, 0}

,

where the coefficients A _xx , A _xy , A _yy , B _x , B _y , and C satisfy the following relation

D={\begin{vmatrix}A_{xx}&A_{xy}\\A_{xy}&A_{yy}\end{vmatrix}}<0

{\ displaystyle D = {\ begin {vmatrix} A_ {xx} & A_ {xy} \\ A_ {xy} & A_ {yy} \ end {vmatrix}} <0}

and

\Delta :={\begin{vmatrix}A_{xx}&A_{xy}&B_{x}\\A_{xy}&A_{yy}&B_{y}\\B_{x}&B_{y}&C\end{vmatrix}}\not =0.

{\ displaystyle \ Delta: = {\ begin {vmatrix} A_ {xx} & A_ {xy} & B_ {x} \\ A_ {xy} & A_ {yy} & B_ {y} \\ B_ {x} & B_ {y} & C \ end {vmatrix}} \ not = 0.}

Canonical View

By moving the center of the hyperbola to the origin and rotating it relative to the center, the hyperbole equation can be reduced to the canonical form

{\frac {{x}^{2}}{a^{2}}}-{\frac {{y}^{2}}{b^{2}}}=1

{\ displaystyle {\ frac {{x} ^ {2}} {a ^ {2}}} - {\ frac {{y} ^ {2}} {b ^ {2}}} = 1}

,

where a is the actual semi-axis of the hyperbola; b - imaginary axis of the hyperbola ^[1] . In this case, the eccentricity is

\varepsilon ={\sqrt {1+{\frac {b^{2}}{a^{2}}}}}.

{\ displaystyle \ varepsilon = {\ sqrt {1 + {\ frac {b ^ {2}} {a ^ {2}}}}}.}

Polar coordinates

Hyperbole in polar coordinates

If the pole is in the focus of the hyperbola, and the vertex of the hyperbola lies on the continuation of the polar axis, then

r={\frac {p}{1-\varepsilon \cos \varphi }}

{\ displaystyle r = {\ frac {p} {1- \ varepsilon \ cos \ varphi}}}

If the pole is in the focus of the hyperbola, and the polar axis is parallel to one of the asymptotes, then

{\frac {1}{r}}={\frac {a}{b^{2}}}\left(1-\cos \theta \right)+{\frac {1}{b}}\sin \theta

{\ displaystyle {\ frac {1} {r}} = {\ frac {a} {b ^ {2}}} \ left (1- \ cos \ theta \ right) + {\ frac {1} {b} } \ sin \ theta}

Parameterization of a hyperbola branch using hyperbolic functions

Parametric Equations

Just as an ellipse can be represented by equations in parametric form, which include trigonometric functions, a hyperbola in a rectangular coordinate system whose center coincides with its center, and the abscissa axis passes through the foci, can be represented by equations in parametric form, which include hyperbolic functions ^[2] .

${\begin{cases}x=\pm a\operatorname {ch} t\\y=b\operatorname {sh} t\end{cases}}\;\;\;-\infty <t<+\infty .$ ${\ displaystyle {\ begin {cases} x = \ pm a \ operatorname {ch} t \\ y = b \ operatorname {sh} t \ end {cases}} \; \; \; - \ infty <t <+ \ infty.}$

In the first equation, the “+” sign corresponds to the right branch of the hyperbola, and “-” corresponds to its left branch.

Properties

Optical property. Light from a source located in one of the foci of the hyperbola is reflected by the second branch of the hyperbola so that the extensions of the reflected rays intersect in the second focus.
- In other words, if $F_{1}$ ${\ displaystyle F_ {1}}$ and $F_{2}$ ${\ displaystyle F_ {2}}$ hyperbole foci, then tangent at any point $X$ ${\ displaystyle X}$ hyperbole is the angle bisector $\angle F_{1}XF_{2}$ ${\ displaystyle \ angle F_ {1} XF_ {2}}$ .
For any point lying on a hyperbole, the ratio of the distances from this point to the focus to the distance from the same point to the directrix is a constant.
A hyperbola has mirror symmetry with respect to the real and imaginary axes, as well as rotational symmetry when rotated through an angle of 180 ° around the center of the hyperbola.
Each hyperbola has a conjugate hyperbola , for which the real and imaginary axes change places, but the asymptotes remain the same. This corresponds to replacing a and b with each other in the formula describing the hyperbola. The conjugate hyperbola is not the result of a rotation of the initial hyperbola by an angle of 90 °; hyperbolas vary in shape when $a\neq b$ ${\ displaystyle a \ neq b}$ .
A segment of a tangent at each point of a hyperbola enclosed between two asymptotes of a hyperbola is divided by a point of tangency in half and cuts off a triangle of constant area from two asymptotes.

Asymptotes

Two conjugate hyperbolas (blue and green) have coincident asymptotes (red). These hyperbolas are single and equilateral, since a = b = 1

For a hyperbola given in canonical form

{\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1

{\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} - {\ frac {y ^ {2}} {b ^ {2}}} = 1}

the equations of two asymptotes have the form:

{\frac {x}{a}}\pm {\frac {y}{b}}=0

{\ displaystyle {\ frac {x} {a}} \ pm {\ frac {y} {b}} = 0}

.

Diameters and Chords

Hyperbole Diameters

The diameter of a hyperbola, like any conical section, is a straight line passing through the midpoints of parallel chords. Each direction of parallel chords has its own conjugate diameter. All diameters of a hyperbola pass through its center. The diameter corresponding to the chords parallel to the imaginary axis is the real axis; the diameter corresponding to the chords parallel to the real axis is the imaginary axis.

Angular coefficient $k$ ${\ displaystyle k}$ parallel chords and slope $k_{1}$ ${\ displaystyle k_ {1}}$ corresponding diameter is related by

k\cdot k_{1}=\varepsilon ^{2}-1={\frac {b^{2}}{a^{2}}}

{\ displaystyle k \ cdot k_ {1} = \ varepsilon ^ {2} -1 = {\ frac {b ^ {2}} {a ^ {2}}}}

If diameter a bisects chords parallel to diameter b , then diameter b bisects chords parallel to diameter a . Such diameters are called mutually conjugate . The main diameters are called mutually conjugate and mutually perpendicular diameters. A hyperbola has only one pair of main diameters - the real and imaginary axis.

Determining the center of a hyperbola

Tangent and Normal

Since the hyperbola is a smooth curve, at each of its points ( x ₀ , y ₀ ) one can draw a tangent and a normal . The equation of the tangent to the hyperbola given by the canonical equation has the form:

{\frac {xx_{0}}{a^{2}}}-{\frac {yy_{0}}{b^{2}}}=1

{\ displaystyle {\ frac {xx_ {0}} {a ^ {2}}} - {\ frac {yy_ {0}} {b ^ {2}}} = 1}

,

or, which is the same

y=y_{0}+{\frac {b^{2}x_{0}}{a^{2}y_{0}}}\left(x-x_{0}\right)

{\ displaystyle y = y_ {0} + {\ frac {b ^ {2} x_ {0}} {a ^ {2} y_ {0}}} left (x-x_ {0} \ right)}

.

Derivation of the tangent equation

The equation of the tangent of an arbitrary flat line has the form

y-y_{0}=y'\left(x_{0},y_{0}\right)\cdot \left(x-x_{0}\right)

{\ displaystyle y-y_ {0} = y '\ left (x_ {0}, y_ {0} \ right) \ cdot \ left (x-x_ {0} \ right)}

The canonical hyperbola equation can be represented as a pair of functions

y=\pm {\sqrt {{\frac {b^{2}}{a^{2}}}x^{2}-b^{2}}}

{\ displaystyle y = \ pm {\ sqrt {{\ frac {b ^ {2}} {a ^ {2}}} x ^ {2} -b ^ {2}}}}

.

Then the derivative of these functions has the form

y'=\pm {\frac {{\frac {b^{2}}{a^{2}}}x}{\sqrt {{\frac {b^{2}}{a^{2}}}x^{2}-b^{2}}}}={\frac {b^{2}}{a^{2}}}{\frac {x}{y}}

{\ displaystyle y '= \ pm {\ frac {{\ frac {b ^ {2}} {a ^ {2}}} x} {\ sqrt {{\ frac {b ^ {2}} {a ^ { 2}}} x ^ {2} -b ^ {2}}}} = {\ frac {b ^ {2}} {a ^ {2}}} {\ frac {x} {y}}}

.

Substituting this equation into the general equation of the tangent, we obtain

y-y_{0}={\frac {b^{2}}{a^{2}}}{\frac {x_{0}}{y_{0}}}\left(x-x_{0}\right)

{\ displaystyle y-y_ {0} = {\ frac {b ^ {2}} {a ^ {2}}} {\ frac {x_ {0}} {y_ {0}}} \ left (x-x_ {0} \ right)}

{\frac {xx_{0}}{a^{2}}}-{\frac {yy_{0}}{b^{2}}}={\frac {x_{0}^{2}}{a^{2}}}-{\frac {y_{0}^{2}}{b^{2}}}=1

{\ displaystyle {\ frac {xx_ {0}} {a ^ {2}}} - {\ frac {yy_ {0}} {b ^ {2}}} = {\ frac {x_ {0} ^ {2 }} {a ^ {2}}} - {\ frac {y_ {0} ^ {2}} {b ^ {2}}} = 1}

The normal equation for a hyperbole has the form:

y=y_{0}-{\frac {a^{2}}{b^{2}}}{\frac {y_{0}}{x_{0}}}\left(x-x_{0}\right)

{\ displaystyle y = y_ {0} - {\ frac {a ^ {2}} {b ^ {2}}} {\ frac {y_ {0}} {x_ {0}}} \ left (x-x_ {0} \ right)}

.

Derivation of the normal equation

The normal equation of an arbitrary flat line has the form

y-y_{0}={\frac {1}{y'\left(x_{0},y_{0}\right)}}\left(x_{0}-x\right)

{\ displaystyle y-y_ {0} = {\ frac {1} {y '\ left (x_ {0}, y_ {0} \ right)}} left (x_ {0} -x \ right)}

.

The canonical hyperbola equation can be represented as a pair of functions

y=\pm {\sqrt {{\frac {b^{2}}{a^{2}}}x^{2}-b^{2}}}

{\ displaystyle y = \ pm {\ sqrt {{\ frac {b ^ {2}} {a ^ {2}}} x ^ {2} -b ^ {2}}}}

.

Then the derivative of these functions has the form

y'=\pm {\frac {{\frac {b^{2}}{a^{2}}}x}{\sqrt {{\frac {b^{2}}{a^{2}}}x^{2}-b^{2}}}}={\frac {b^{2}}{a^{2}}}{\frac {x}{y}}

{\ displaystyle y '= \ pm {\ frac {{\ frac {b ^ {2}} {a ^ {2}}} x} {\ sqrt {{\ frac {b ^ {2}} {a ^ { 2}}} x ^ {2} -b ^ {2}}}} = {\ frac {b ^ {2}} {a ^ {2}}} {\ frac {x} {y}}}

.

Substituting this equation into the general normal equation, we obtain

y-y_{0}=-{\frac {a^{2}}{b^{2}}}{\frac {y_{0}}{x_{0}}}\left(x-x_{0}\right)

{\ displaystyle y-y_ {0} = - {\ frac {a ^ {2}} {b ^ {2}}} {\ frac {y_ {0}} {x_ {0}}} \ left (x- x_ {0} \ right)}

.

Curvature and Evolution

Hyperbole is shown in blue. Green color indicates the evolution of the right branch of this hyperbola (evolution of the left branch outside the figure. Red circle shows the circle corresponding to the curvature of the hyperbola at its vertex)

The curvature of a hyperbola at each of its points ( x , y ) is determined from the expression:

K={\frac {ab}{\left({\frac {a^{2}}{b^{2}}}y^{2}+{\frac {b^{2}}{a^{2}}}x^{2}\right)^{3/2}}}

{\ displaystyle K = {\ frac {ab} {\ left ({\ frac {a ^ {2}} {b ^ {2}}} y ^ {2} + {\ frac {b ^ {2}} { a ^ {2}}} x ^ {2} \ right) ^ {3/2}}}}

.

Accordingly, the radius of curvature has the form:

R={\frac {1}{K}}={\frac {\left({\frac {a^{2}}{b^{2}}}y^{2}+{\frac {b^{2}}{a^{2}}}x^{2}\right)^{3/2}}{ab}}

{\ displaystyle R = {\ frac {1} {K}} = {\ frac {\ left ({\ frac {a ^ {2}} {b ^ {2}}} y ^ {2} + {\ frac {b ^ {2}} {a ^ {2}}} x ^ {2} \ right) ^ {3/2}} {ab}}}

.

In particular, at the point ( a , 0 ), the radius of curvature is

R\left(a,0\right)={\frac {b^{2}}{a}}=p

{\ displaystyle R \ left (a, 0 \ right) = {\ frac {b ^ {2}} {a}} = p}

.

Derivation of the formula for the radius of curvature

The formula for the radius of curvature of a flat line, specified parametrically, has the form:

R_{c}={\frac {\left(x'^{2}\ +y'^{2}\right)^{3/2}}{\left|x'y''-x''y'\right|}}

{\ displaystyle R_ {c} = {\ frac {\ left (x '^ {2} \ + y' ^ {2} \ right) ^ {3/2}} {\ left | x'y '' - x '' y '\ right |}}}

.

We use the parametric representation of the hyperbola:

{\begin{cases}x=a\cdot \mathrm {ch} \,(t)\\y=b\cdot \mathrm {sh} \,(t)\end{cases}}

{\ displaystyle {\ begin {cases} x = a \ cdot \ mathrm {ch} \, (t) \\ y = b \ cdot \ mathrm {sh} \, (t) \ end {cases}}}

Then, the first derivative of x and y with respect to t has the form

{\begin{cases}x'=a\cdot \mathrm {sh} \,(t)={\frac {a}{b}}y\\y'=b\cdot \mathrm {ch} \,(t)={\frac {b}{a}}x\end{cases}}

{\ displaystyle {\ begin {cases} x '= a \ cdot \ mathrm {sh} \, (t) = {\ frac {a} {b}} y \\ y' = b \ cdot \ mathrm {ch} \, (t) = {\ frac {b} {a}} x \ end {cases}}}

,

and the second derivative is

{\begin{cases}x''=a\cdot \mathrm {ch} \,(t)=x\\y''=b\cdot \mathrm {sh} \,(t)=y\end{cases}}

{\ displaystyle {\ begin {cases} x '' = a \ cdot \ mathrm {ch} \, (t) = x \\ y '' = b \ cdot \ mathrm {sh} \, (t) = y \ end {cases}}}

Substituting these values in the formula for curvature, we obtain:

R_{c}={\frac {\left({\frac {a^{2}}{b^{2}}}y^{2}\ +{\frac {b^{2}}{a^{2}}}x^{2}\right)^{3/2}}{\left|a{\frac {y^{2}}{b}}-b{\frac {x^{2}}{a}}\right|}}={\frac {\left({\frac {a^{2}}{b^{2}}}y^{2}\ +{\frac {b^{2}}{a^{2}}}x^{2}\right)^{3/2}}{ab\left|{\frac {y^{2}}{b}}-{\frac {x^{2}}{a}}\right|}}={\frac {\left({\frac {a^{2}}{b^{2}}}y^{2}\ +{\frac {b^{2}}{a^{2}}}x^{2}\right)^{3/2}}{ab}}

{\ displaystyle R_ {c} = {\ frac {\ left ({\ frac {a ^ {2}} {b ^ {2}}} y ^ {2} \ + {\ frac {b ^ {2}} {a ^ {2}}} x ^ {2} \ right) ^ {3/2}} {\ left | a {\ frac {y ^ {2}} {b}} - b {\ frac {x ^ {2}} {a}} \ right |}} = {\ frac {\ left ({\ frac {a ^ {2}} {b ^ {2}}} y ^ {2} \ + {\ frac { b ^ {2}} {a ^ {2}}} x ^ {2} \ right) ^ {3/2}} {ab \ left | {\ frac {y ^ {2}} {b}} - { \ frac {x ^ {2}} {a}} \ right |}} = {\ frac {\ left ({\ frac {a ^ {2}} {b ^ {2}}} y ^ {2} \ + {\ frac {b ^ {2}} {a ^ {2}}} x ^ {2} \ right) ^ {3/2}} {ab}}}

.

The coordinates of the centers of curvature are given by a pair of equations:

{\begin{cases}x_{c}={\frac {x^{3}}{a^{2}}}\left(1+{\frac {b^{2}}{a^{2}}}\right)\\y_{c}=-{\frac {y^{3}}{b^{2}}}\left(1+{\frac {a^{2}}{b^{2}}}\right)\end{cases}}

{\ displaystyle {\ begin {cases} x_ {c} = {\ frac {x ^ {3}} {a ^ {2}}} \ left (1 + {\ frac {b ^ {2}} {a ^ {2}}} \ right) \\ y_ {c} = - {\ frac {y ^ {3}} {b ^ {2}}} \ left (1 + {\ frac {a ^ {2}} { b ^ {2}}} \ right) \ end {cases}}}

Substituting in the last system of equations instead of x and y their values from the parametric representation of the hyperbola, we obtain a pair of equations defining a new curve consisting of the centers of curvature of the hyperbola. This curve is called the hyperbola evolute .

{\begin{cases}x=\pm a\,\mathrm {ch} ^{3}\,t\left(1+{\frac {b^{2}}{a^{2}}}\right)\\y=b\,\mathrm {sh} ^{3}\,t\left(1+{\frac {a^{2}}{b^{2}}}\right)\end{cases}}

{\ displaystyle {\ begin {cases} x = \ pm a \, \ mathrm {ch} ^ {3} \, t \ left (1 + {\ frac {b ^ {2}} {a ^ {2}} } \ right) \\ y = b \, \ mathrm {sh} ^ {3} \, t \ left (1 + {\ frac {a ^ {2}} {b ^ {2}}} \ right) \ end {cases}}}

Elliptical coordinate system

Summary

Hyperbole is a sinusoidal spiral at $n=-2$ ${\ displaystyle n = -2}$ ;

Application

The family of confocal ( confocal ) hyperbolas together with the family of confocal ellipses form a two-dimensional elliptical coordinate system .

Other orthogonal two-dimensional coordinate systems constructed using hyperbolas can be obtained using other conformal transformations. For example, the transformation w = z ² maps the Cartesian coordinates into two families of orthogonal hyperbolas.

By inverting a hyperbola with a center lying in its own center, in focus or at the apex, one can obtain a lemniscate Bernoulli , a snail of Pascal, or a stanoid , respectively.

Hyperbolas on the vertical sundial of the Palace of the Grand Dukes of Lithuania in Vilnius , a round shadow of the top of the gnomon is visible, describing the hyperbola during the day

Hyperbolas can be seen on many sundials . Throughout any day of the year, the Sun describes a circle on the celestial sphere , and its rays incident on the top of the gnomon of a sundial describe a cone of light. The line of intersection of this cone with the plane of a horizontal or vertical sundial is a conical section . At the most populated latitudes and in most of the year, this conical section is a hyperbole. The sundial often shows the lines described by the shadow from the top of the gnomon during the day for several days of the year (for example, days of the summer and winter solstices), so you can often see certain hyperbols on them, the form of which is different for different days of the year and different latitudes .

Notes

↑ Schneider V.E. Short course in higher mathematics . - Ripol Classic. - ISBN 9785458255349 .
↑ Погорелов А. В. Геометрия. — М. : Наука , 1983. — С. 15—16. — 288 с.

Literature

Бронштейн И. Гипербола // Квант . — 1975. — № 3 .
Граве Д. А. Гиперболы // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). - SPb. , 1890-1907.
Математическая энциклопедия (в 5-и томах). М.: Советская энциклопедия , 1982.
Маркушевич А. И. Замечательные кривые // Популярные лекции по математике . — Гостехиздат, 1952. — Вып. 4 . Архивировано 14 сентября 2008 года.

[1] Schneider V.E. Short course in higher mathematics . - Ripol Classic. - ISBN 9785458255349 .

[2] Погорелов А. В. Геометрия. — М. : Наука , 1983. — С. 15—16. — 288 с.