Cone

straight circular cone

straight and oblique circular cones with equal base and height: they have the same volume

truncated straight circular cone

The cone (from the Greek Greek κώνος “pine cone” ^[1] ) is a body in Euclidean space obtained by combining all the rays emanating from one point (the top of the cone) and passing through a flat surface. Sometimes a cone is a part of such a body that has a limited volume and is obtained by combining all the segments connecting the vertex and the points of a flat surface (the latter in this case is called the base of the cone, and the cone is called leaning on this base). If the base of the cone is a polygon , such a cone is a pyramid .

Related Definitions

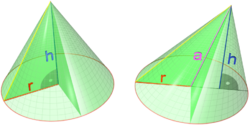
generatrix of the cone - a segment connecting the top and the border of the base.
forming (or lateral ) surface of the cone - the union of the generators of the cone; the forming surface of the cone is a conical surface .
cone height - a segment lowered perpendicular from the top to the base plane (as well as the length of such a segment).
the cone angle is the angle between two opposite generators (the angle at the apex of the cone, inside the cone).
taper - the ratio of the height and diameter of the base of the cone.
straight cone - a cone whose base has a center of symmetry (for example, is a circle or an ellipse ) and the orthogonal projection of the cone vertex onto the plane of the base coincides with this center; the straight line connecting the top and center of the base is called the axis of the cone .
oblique (or inclined ) cone - a cone in which the orthogonal projection of the vertex onto the base does not coincide with its center of symmetry.
circular cone - a cone whose base is a circle.
a straight circular cone (often called simply a cone) can be obtained by rotating a right triangle around a line containing a leg (this line represents the axis of the cone).
a cone based on an ellipse , parabola or hyperbola is called an elliptic , parabolic and hyperbolic cone , respectively: the last two have infinite volume.
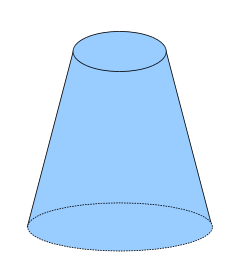
truncated cone or conical layer - part of the cone lying between the base and the plane parallel to the base and located between the top and the base.

Properties

If the area of the base is finite, then the volume of the cone is also finite and equal to one third of the product of height by the area of the base.

V={1 \over 3}SH,

{\ displaystyle V = {1 \ over 3} SH,}

where S is the area of the base, H is the height. Thus, all cones based on a given base (finite area) and having a vertex located on a given plane parallel to the base have equal volume, since their heights are equal.

The center of gravity of any cone with a finite volume lies a quarter of the height from the base.
The solid angle at the apex of a straight circular cone is

2\pi \left(1-\cos {\alpha  \over 2}\right),

{\ displaystyle 2 \ pi \ left (1- \ cos {\ alpha \ over 2} \ right),}

where α is the angle of the cone.

The area of the lateral surface of such a cone is

S=\pi Rl,

{\ displaystyle S = \ pi Rl,}

and the total surface area (i.e. the sum of the areas of the side surface and the base)

S=\pi R(l+R),

{\ displaystyle S = \ pi R (l + R),}

where R is the radius of the base,

l={\sqrt {R^{2}+H^{2}}}

{\ displaystyle l = {\ sqrt {R ^ {2} + H ^ {2}}}}

- the length of the generatrix.

The volume of a circular (not necessarily straight) cone is

V={1 \over 3}\pi R^{2}H.

{\ displaystyle V = {1 \ over 3} \ pi R ^ {2} H.}

For a truncated circular cone (not necessarily straight), the volume is:

V={1 \over 3}\pi H(R^{2}+Rr+r^{2}),

{\ displaystyle V = {1 \ over 3} \ pi H (R ^ {2} + Rr + r ^ {2}),}

Where

R

{\ displaystyle R}

and

r

{\ displaystyle r}

- the radii of the lower and upper bases, respectively

H

{\ displaystyle H}

- height from the plane of the lower base to the upper base.

For an arbitrary truncated cone (not necessarily straight and circular), the volume is:

V={1 \over 3}(H_{2}S_{2}-H_{1}S_{1}),

{\ displaystyle V = {1 \ over 3} (H_ {2} S_ {2} -H_ {1} S_ {1}),}

Where

S_{1}

{\ displaystyle S_ {1}}

and

S_{2}

{\ displaystyle S_ {2}}

- area respectively of the upper (closest to the top) and lower bases,

H_{1}

{\ displaystyle H_ {1}}

and

H_{2}

{\ displaystyle H_ {2}}

- the distance from the plane, respectively, of the upper and lower bases to the top.

The intersection of a plane with a straight circular cone is one of the conical sections (in non-degenerate cases - an ellipse , parabola or hyperbola , depending on the position of the secant plane).

The equation of a direct circular cone

Equations defining the lateral surface of a straight circular cone with a 2 углом angle of apex, a vertex at the origin, and an axis coinciding with the Oz axis:

In a spherical coordinate system with coordinates ( r , φ, θ) :

\theta =\Theta .

{\ displaystyle \ theta = \ Theta.}

In a cylindrical coordinate system with coordinates ( r , φ, z ) :

z=r\cdot \operatorname {ctg} \Theta

{\ displaystyle z = r \ cdot \ operatorname {ctg} \ Theta}

or

r=z\cdot \operatorname {tg} \Theta .

{\ displaystyle r = z \ cdot \ operatorname {tg} \ Theta.}

In a Cartesian coordinate system with coordinates ( x , y , z ) :

z=\pm {\sqrt {x^{2}+y^{2}}}\cdot \operatorname {ctg} \Theta .

{\ displaystyle z = \ pm {\ sqrt {x ^ {2} + y ^ {2}}} \ cdot \ operatorname {ctg} \ Theta.}

This equation in canonical form is written as

{\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{a^{2}}}-{\frac {z^{2}}{c^{2}}}=0,

{\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} + {\ frac {y ^ {2}} {a ^ {2}}} - {\ frac {z ^ {2} } {c ^ {2}}} = 0,}

where the constants a , c are determined by the proportion

c/a=\cos \Theta /\sin \Theta .

{\ displaystyle c / a = \ cos \ Theta / \ sin \ Theta.}

This shows that the lateral surface of a straight circular cone is a second-order surface (it is called a conical surface ). In general, a second-order conical surface is supported by an ellipse; in a suitable Cartesian coordinate system (the axes Ox and Oy are parallel to the axes of the ellipse, the vertex of the cone coincides with the origin, the center of the ellipse lies on the axis Oz ), its equation has the form

{\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=0,

{\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} + {\ frac {y ^ {2}} {b ^ {2}}} - {\ frac {z ^ {2} } {c ^ {2}}} = 0,}

moreover, a / c and b / c are equal to the semiaxes of the ellipse. In the most general case, when the cone rests on an arbitrary flat surface, it can be shown that the equation of the lateral surface of the cone (with the vertex at the origin) is given by the equation

f(x,y,z)=0,

{\ displaystyle f (x, y, z) = 0,}

where is the function

f(x,y,z)

{\ displaystyle f (x, y, z)}

is homogeneous , that is, satisfying the condition

f(\alpha x,\alpha y,\alpha z)=\alpha ^{n}f(x,y,z)

{\ displaystyle f (\ alpha x, \ alpha y, \ alpha z) = \ alpha ^ {n} f (x, y, z)}

for any real number α .

Sweep

Sweep of a straight circular cone

A straight circular cone as a body of revolution is formed by a rectangular triangle rotating around one of the legs, where h is the height of the cone from the center of the base to the top - is the leg of the right triangle around which rotation occurs. The second leg of the right triangle r is the radius at the base of the cone. The hypotenuse of a right triangle is the l -forming cone.

In creating the development of the cone, only two values r and l can be used. The radius of the base r determines in the scan the circle of the base of the cone, and the sector of the side surface of the cone determines the generatrix of the side surface l , which is the radius of the sector of the side surface. Sector angle $\varphi$ ${\ displaystyle \ varphi}$ in the development of the lateral surface of the cone is determined by the formula:

φ = 360 ° ( r / l ) .

Variations and generalizations

In algebraic geometry, a cone is an arbitrary subset $K$ ${\ displaystyle K}$ vector space $V$ ${\ displaystyle V}$ over the field $F$ ${\ displaystyle F}$ for which for any $\lambda \in F$ ${\ displaystyle \ lambda \ in F}$
$\lambda K=K.$ ${\ displaystyle \ lambda K = K.}$
In topology, a cone over a topological space X is a quotient space $X\times [0,\infty )$ ${\ displaystyle X \ times [0, \ infty)}$ in relation to equivalence $(x,0)\sim (y,0).$ ${\ displaystyle (x, 0) \ sim (y, 0).}$

Notes

↑ "I κῶνος"

Literature

The article "Cone" in the Mathematical Encyclopedia .
Korn G., Korn T. Handbook of mathematics for scientists and engineers. M .: Nauka, 1973.

[1] "I κῶνος"