Count Cayley

Count Cayley - a graph that is built on a group with a dedicated system of generators. Named after Arthur Cayley .

Definition

Let a discrete group be given $G$ ${\ displaystyle G}$ $G$ and system of generators $S$ ${\ displaystyle S}$ $S$ .

Suppose $S=S^{-1}$ ${\ displaystyle S = S ^ {- 1}}$ $S=S^{{-1}}$ , that is, for each $s\in S,\exists s^{-1}\in S$ ${\ displaystyle s \ in S, \ exists s ^ {- 1} \ in S}$ $s\in S,\exists s^{{-1}}\in S$ .

Earl Cayley Group $G$ ${\ displaystyle G}$ $G$ according to the system of generators $S$ ${\ displaystyle S}$ $S$ is a graph whose vertices are the elements of the group and the element $g$ ${\ displaystyle g}$ $g$ connected by an edge exactly with those elements that are obtained by multiplication $g$ ${\ displaystyle g}$ $g$ per element from $S$ ${\ displaystyle S}$ $S$ .

Note: In case $S\not =S^{-1}$ ${\ displaystyle S \ not = S ^ {- 1}}$ $S\not =S^{{-1}}$ instead $S$ ${\ displaystyle S}$ $S$ take a pool $S\cup S^{-1}$ ${\ displaystyle S \ cup S ^ {- 1}}$ $S\cup S^{{-1}}$ .

Examples

Cayley graph of a free group with two generators a and b
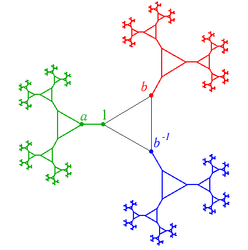
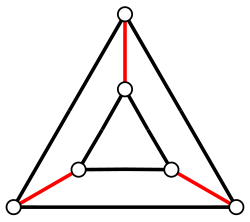
Count Cayley free artwork $\mathbb {Z} _{2}*\mathbb {Z} _{3}$ ${\ displaystyle \ mathbb {Z} _ {2} * \ mathbb {Z} _ {3}}$ $\mathbb{Z } _{2}*\mathbb{Z } _{3}$
Count Cayley direct artwork $\mathbb {Z} _{2}\times \mathbb {Z} _{3}$ ${\ displaystyle \ mathbb {Z} _ {2} \ times \ mathbb {Z} _ {3}}$

Count Cayley

Definition

Examples

See also

More articles: