Circle

Circumference (C), its center (O) , radius (R) and diameter (D)

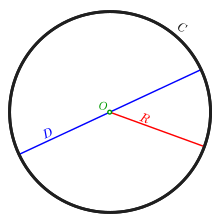
A circle is a closed plane curve that consists of all points on the plane equidistant from a given point ^[1] : this point is called the center of the circle . A line connecting the center to a point in a circle is called a radius ; the radius is also called the length of this segment. The circle divides the plane into two parts ^[2] - finite internal and infinite external: the number of points in these areas is equal. The inside of a circle is called a circle ; boundary points (that is, the circle itself), depending on the approach, the circle may or may not include.

Drawing a circle with a compass

Practical construction of a circle is possible using a compass .

A circle of zero radius (a degenerate circle) is a point, then this case is excluded from consideration, unless otherwise specified.

A single circle - with a radius equal to one: one of the main objects of trigonometry .

Further everywhere the letter $R$ ${\ displaystyle R}$ $R$ denotes the radius of the circle.

Chords, Arcs, and Tangents

1 - secant , 2 - AB chord (marked in red), 3 - segment (marked in green), 4 - arc
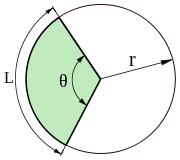
Circle sectors

A straight line can have at most two common points with a circle.

A line intersecting a circle at two different points is called a secant . A section of a secant located inside a circle is called a chord . A chord passing through the center of a circle is called a diameter ; the same term is used for its length. The diameter is twice the radius: $D=2R,$ ${\ displaystyle D = 2R,}$ it divides the circle into two equal parts and therefore is its axis of symmetry . The diameter is larger than any other chord ^[3] .

A chord breaks a circle into two parts, called segments of a circle . Two different radii also divide the circle into two parts, called sectors of the circle (see figures) ^[3] .

Any two mismatched points of a circle divide it into two parts. Each of these parts is called an arc of a circle . An arc is called a semicircle if the segment connecting its ends is a diameter.

For a given circle, the following properties hold ^[3] .

The chords equally spaced from the center are equal. Conversely, if two chords are equal in length, then they are equally distant from the center.
Equal chords correspond to equal arcs, and vice versa.

Tangent to a circle

A line that has exactly one common point with a circle is called a tangent to the circle, and their common point is called the point of tangency of the line and the circle. A tangent to a circle is always perpendicular to its radius (and diameter) drawn at the point of tangency. That is, the radius is at the same time normal to the circle ^[4] .

The segments of the tangents to the circle drawn from one point that does not lie on the circle are equal and equal angles with a straight line passing through this point and the center of the circle.

Corners

The inscribed angle θ is equal to half the magnitude of the central angle 2 θ , based on the same arc (pink)
To calculate the length of the arc and chord

The central angle is the angle with the apex in the center of the circle. The central angle can be taken as the angular measure of the arc on which it rests. The central angle formed by an arc of a circle equal in length to the radius is taken in mathematics as the unit of measurement of angles, and is called the radian .

It follows from the definition of a radian that the length $L$ ${\ displaystyle L}$ any arc of a circle is connected with a central angle $\theta$ ${\ displaystyle \ theta}$ based on this arc, a simple relation ^[5] : $L=R\theta .$ ${\ displaystyle L = R \ theta.}$ (the length of the chord contracting the same arc is $2R\sin {\theta \over 2}<L$ ${\ displaystyle 2R \ sin {\ theta \ over 2} <L}$ ) Since the circumference is $2\pi R$ ${\ displaystyle 2 \ pi R}$ , with an increase in the angle, the value of its radian measure varies from 0 to $2\pi .$ ${\ displaystyle 2 \ pi.}$

An inscribed angle is an angle whose vertex lies on a circle, and the sides intersect this circle.

The external angle for the inscribed angle is the angle formed by one side and the continuation of the other side of the inscribed angle (brown angle θ in the figure). The external angle for the inscribed angle is equal to the inscribed angle, based on the same chord from the other side.

The angle between the circle and the line is the angle between the secant line and one of the two tangents to the circle at the intersection of the line and the circle.

Properties of inscribed corners :

The inscribed angle is either equal to half of the central angle, resting on its arc, or complements half of this angle to 180 °. An inscribed angle, based on an arc half a circle long, is always straight (equal to 90 °).
The inscribed angle does not change its value when its vertex moves along the circle.
Two inscribed angles based on the same arc are equal.

Other properties:

The angle between two secants drawn from a point lying outside the circle is equal to the half - difference of the measures of the arcs lying between the secants.
The angle between the intersecting chords is equal to the half-sum of the measures of the arc lying in the corner, and the arc opposite it.
The angle between the tangent and the chord, which have a common point, is equal to half the angular measure of the arc contracted by the chord.

Properties

Isoperimetric inequality : Of all the closed curves of a given length, the circle limits the region of maximum area.
Through three points that do not lie on one straight line, you can draw a circle, and moreover, only one.
Two circles are said to be tangent if they have a single common point. The tangent point of two circles lies on a straight line passing through their centers.
Secant theorem : If through an arbitrary point $E$ ${\ displaystyle E}$ the secant is drawn, then the product of the distances from this point to the intersection points of the secant with the circle does not depend on the choice of the secant (and is equal to the absolute value of the degree of the point relative to the circle ). If the point $E$ ${\ displaystyle E}$ lies outside the circle, then a tangent can be drawn from it to the circle. The square of the length of the tangent segment to the point of contact will be equal to the same value.

As a special case of the previous one, when two chords intersect at an arbitrary point $E$ ${\ displaystyle E}$ segments are obtained whose product of the lengths of one chord is equal to the corresponding product of the other (see figure), i.e. $AE\cdot EB=CE\cdot ED$ ${\ displaystyle AE \ cdot EB = CE \ cdot ED}$ .

AE\cdot EB=CE\cdot ED

{\ displaystyle AE \ cdot EB = CE \ cdot ED}

Formula Summary

If the radius of the circle is 1, then its circle is 2π.

Circumference:

C=2\pi R=\pi D.

{\ displaystyle C = 2 \ pi R = \ pi D.}

Circle radius:

R={\frac {C}{2\pi }}={\frac {D}{2}}.

{\ displaystyle R = {\ frac {C} {2 \ pi}} = {\ frac {D} {2}}.}

Circle Diameter:

D={\frac {C}{\pi }}=2R.

{\ displaystyle D = {\ frac {C} {\ pi}} = 2R.}

Circle area of radius R :

S=\pi R^{2}={\frac {\pi D^{2}}{4}}.

{\ displaystyle S = \ pi R ^ {2} = {\ frac {\ pi D ^ {2}} {4}}.}

The area of the sector bounded by the central angle α , measured in degrees, with radius R :

S=\pi R^{2}{\frac {\alpha }{360^{\circ }}}.

{\ displaystyle S = \ pi R ^ {2} {\ frac {\ alpha} {360 ^ {\ circ}}}.}

Area of a segment bounded by an arc of a circle, central angle α , chord:

S=\pi R^{2}{\frac {\alpha }{360^{\circ }}}-{\frac {R^{2}\sin \alpha }{2}}.

{\ displaystyle S = \ pi R ^ {2} {\ frac {\ alpha} {360 ^ {\ circ}}} - {\ frac {R ^ {2} \ sin \ alpha} {2}}.}

History

The circle, along with the straight line, is the most common curve in almost all areas of human activity. The history of its research and application goes back to antiquity; Of particular importance was the invention of the wheel . Ancient scientists considered straight lines and circles as the only example of "perfect" curves, therefore in geometry only constructions using a compass and a ruler were considered permissible, and the motion of the planets was modeled as the superposition of rotations around circles . The theory of circles is the subject of the third book of the Beginning of Euclid .

It was also discovered in antiquity that the ratio of the circumference of a circle to its diameter ( number π ) is the same for all circles. The historically important topic of centuries of research has been the refinement of this relationship, as well as attempts to solve the problem of “ squaring the circle ”. Further development of the theory of circles led to the creation of trigonometry , the theory of oscillations, and many other practically important branches of science and technology.

A circle is obtained as a section of a cone by a plane perpendicular to its axis

Analytical geometry of circles

From the point of view of analytic geometry , a circle is a simple plane algebraic curve of the second order . A circle is a special case of an ellipse in which the semi-axes are equal, and therefore the circle refers to conical sections .

Cartesian coordinates

Circle of radius r = 1, center ( a , b ) = (1.2, −0.5)

The general equation of the circle is written as:

x^{2}+y^{2}+Ax+By+C=0,

{\ displaystyle x ^ {2} + y ^ {2} + Ax + By + C = 0,}

or

\left(x-x_{0}\right)^{2}+\left(y-y_{0}\right)^{2}=R^{2},

{\ displaystyle \ left (x-x_ {0} \ right) ^ {2} + \ left (y-y_ {0} \ right) ^ {2} = R ^ {2},}

Where

2x_{0}=-A,\;2y_{0}=-B,\;2R={\sqrt {A^{2}+B^{2}-4C}}.

{\ displaystyle 2x_ {0} = - A, \; 2y_ {0} = - B, \; 2R = {\ sqrt {A ^ {2} + B ^ {2} -4C}}.}

Point $\left(x_{0},y_{0}\right)$ ${\ displaystyle \ left (x_ {0}, y_ {0} \ right)}$ Is the center of the circle, $R$ ${\ displaystyle R}$ Is its radius.

Radius Circle Equation $R$ ${\ displaystyle R}$ centered at the origin :

x^{2}+y^{2}=R^{2}.

{\ displaystyle x ^ {2} + y ^ {2} = R ^ {2}.}

Equation of a circle passing through points $\left(x_{1},y_{1}\right),\left(x_{2},y_{2}\right),\left(x_{3},y_{3}\right),$ ${\ displaystyle \ left (x_ {1}, y_ {1} \ right), \ left (x_ {2}, y_ {2} \ right), \ left (x_ {3}, y_ {3} \ right) ,}$ not lying on one straight line (using the determinant ):

{\begin{vmatrix}x^{2}+y^{2}&x&y&1\\x_{1}^{2}+y_{1}^{2}&x_{1}&y_{1}&1\\x_{2}^{2}+y_{2}^{2}&x_{2}&y_{2}&1\\x_{3}^{2}+y_{3}^{2}&x_{3}&y_{3}&1\end{vmatrix}}=0.

{\ displaystyle {\ begin {vmatrix} x ^ {2} + y ^ {2} & x & y & 1 \\ x_ {1} ^ {2} + y_ {1} ^ {2} & x_ {1} & y_ {1} & 1 \ \ x_ {2} ^ {2} + y_ {2} ^ {2} & x_ {2} & y_ {2} & 1 \\ x_ {3} ^ {2} + y_ {3} ^ {2} & x_ {3} & y_ {3} & 1 \ end {vmatrix}} = 0.}

Then, in the explicit form, the coordinates of the center of the circle are determined by the formulas:

x_{0}=-{\frac {1}{2}}{\frac {y_{1}(x_{2}^{2}+y_{2}^{2}-x_{3}^{2}-y_{3}^{2})+y_{2}(x_{3}^{2}+y_{3}^{2}-x_{1}^{2}-y_{1}^{2})+y_{3}(x_{1}^{2}+y_{1}^{2}-x_{2}^{2}-y_{2}^{2})}{x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})}}

{\ displaystyle x_ {0} = - {\ frac {1} {2}} {\ frac {y_ {1} (x_ {2} ^ {2} + y_ {2} ^ {2} -x_ {3} ^ {2} -y_ {3} ^ {2}) + y_ {2} (x_ {3} ^ {2} + y_ {3} ^ {2} -x_ {1} ^ {2} -y_ {1 } ^ {2}) + y_ {3} (x_ {1} ^ {2} + y_ {1} ^ {2} -x_ {2} ^ {2} -y_ {2} ^ {2})} { x_ {1} (y_ {2} -y_ {3}) + x_ {2} (y_ {3} -y_ {1}) + x_ {3} (y_ {1} -y_ {2})}}}

y_{0}={\frac {1}{2}}{\frac {x_{1}(x_{2}^{2}+y_{2}^{2}-x_{3}^{2}-y_{3}^{2})+x_{2}(x_{3}^{2}+y_{3}^{2}-x_{1}^{2}-y_{1}^{2})+x_{3}(x_{1}^{2}+y_{1}^{2}-x_{2}^{2}-y_{2}^{2})}{x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})}}

{\ displaystyle y_ {0} = {\ frac {1} {2}} {\ frac {x_ {1} (x_ {2} ^ {2} + y_ {2} ^ {2} -x_ {3} ^ {2} -y_ {3} ^ {2}) + x_ {2} (x_ {3} ^ {2} + y_ {3} ^ {2} -x_ {1} ^ {2} -y_ {1} ^ {2}) + x_ {3} (x_ {1} ^ {2} + y_ {1} ^ {2} -x_ {2} ^ {2} -y_ {2} ^ {2})} {x_ {1} (y_ {2} -y_ {3}) + x_ {2} (y_ {3} -y_ {1}) + x_ {3} (y_ {1} -y_ {2})}}}

The circle can also be described using the parametric equation :

{\begin{cases}x=x_{0}+R\cos \varphi \\y=y_{0}+R\sin \varphi \end{cases}},\;\;\;0\leqslant \varphi <2\pi .

{\ displaystyle {\ begin {cases} x = x_ {0} + R \ cos \ varphi \\ y = y_ {0} + R \ sin \ varphi \ end {cases}}, \; \; \; 0 \ leqslant \ varphi <2 \ pi.}

In a Cartesian coordinate system, a circle is not a function graph , but it can be described as a union of the graphs of the two following functions:

y=y_{0}\pm {\sqrt {R^{2}-(x-x_{0})^{2}}}.

{\ displaystyle y = y_ {0} \ pm {\ sqrt {R ^ {2} - (x-x_ {0}) ^ {2}}}.

If the center of the circle coincides with the origin, the functions take the form:

y=\pm {\sqrt {R^{2}-x^{2}}}.

{\ displaystyle y = \ pm {\ sqrt {R ^ {2} -x ^ {2}}}.}

Polar coordinates

Circle of radius $R$ ${\ displaystyle R}$ centered at $\left(\rho _{0},\phi _{0}\right)$ ${\ displaystyle \ left (\ rho _ {0}, \ phi _ {0} \ right)}$ :

\rho ^{2}-2\rho \,\rho _{0}\cos \left(\phi -\phi _{0}\right)+\rho _{0}^{2}=R^{2}.

{\ displaystyle \ rho ^ {2} -2 \ rho \, \ rho _ {0} \ cos \ left (\ phi - \ phi _ {0} \ right) + \ rho _ {0} ^ {2} = R ^ {2}.}

If the polar coordinates of the center of the circle $\rho _{0}=R,\;\phi _{0}=\alpha ,$ ${\ displaystyle \ rho _ {0} = R, \; \ phi _ {0} = \ alpha,}$ then the circle passing through the origin is described by the equation:

\rho (\varphi )=2R\cos \,(\varphi -\alpha ),\;\;\;\alpha -{\frac {\pi }{2}}\leqslant \varphi \leqslant \alpha +{\frac {\pi }{2}}.

{\ displaystyle \ rho (\ varphi) = 2R \ cos \, (\ varphi - \ alpha), \; \; \; \ alpha - {\ frac {\ pi} {2}} \ leqslant \ varphi \ leqslant \ alpha + {\ frac {\ pi} {2}}.}

If the center is the origin, then the equation will have the form

\rho =R.

{\ displaystyle \ rho = R.}

Complex plane

On the complex plane, the circle is given by the formula:

\left|z-z_{0}\right|=R

{\ displaystyle \ left | z-z_ {0} \ right | = R}

or in parametric form

z=z_{0}+Re^{it},\,t\in \mathbb {R} .

{\ displaystyle z = z_ {0} + Re ^ {it}, \, t \ in \ mathbb {R}.}

Circles in space

In space, a circle of radius $R$ ${\ displaystyle R}$ centered at $M_{0}(x_{0},y_{0},z_{0})$ ${\ displaystyle M_ {0} (x_ {0}, y_ {0}, z_ {0})}$ can be defined as the contour of the diametrical section of a sphere

(x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}=R^{2}

{\ displaystyle (x-x_ {0}) ^ {2} + (y-y_ {0}) ^ {2} + (z-z_ {0}) ^ {2} = R ^ {2}}

plane

a\cdot (x-x_{0})+b\cdot (y-y_{0})+c\cdot (z-z_{0})=0

{\ displaystyle a \ cdot (x-x_ {0}) + b \ cdot (y-y_ {0}) + c \ cdot (z-z_ {0}) = 0}

,

Where $a, b, c$ ${\ displaystyle a, b, c}$ - parameters not simultaneously equal to zero; that is, all points lying on a given circle are solutions of the system

{\begin{cases}(x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}=R^{2},\\a{\cdot }(x-x_{0})+b{\cdot }(y-y_{0})+c{\cdot }(z-z_{0})=0.\end{cases}}

{\ displaystyle {\ begin {cases} (x-x_ {0}) ^ {2} + (y-y_ {0}) ^ {2} + (z-z_ {0}) ^ {2} = R ^ {2}, \\ a {\ cdot} (x-x_ {0}) + b {\ cdot} (y-y_ {0}) + c {\ cdot} (z-z_ {0}) = 0. \ end {cases}}}

For example, when $a=c\neq 0$ ${\ displaystyle a = c \ neq 0}$ solutions of this system can be defined parametrically as follows:

{\begin{cases}x=x_{0}+{\dfrac {R}{\sqrt {a^{2}+c^{2}}}}\cdot \!\left(c\cdot \cos t-{\dfrac {a\cdot b\cdot \sin t}{\sqrt {a^{2}+b^{2}+c^{2}}}}\right)\!,\\[10pt]y=y_{0}+{\dfrac {R\cdot {\sqrt {a^{2}+c^{2}}}}{\sqrt {a^{2}+b^{2}+c^{2}}}}\cdot \sin t,\\[10pt]z=z_{0}-{\dfrac {R}{\sqrt {a^{2}+c^{2}}}}\cdot \!\left(a\cdot \cos t+{\dfrac {b\cdot c\cdot \sin t}{\sqrt {a^{2}+b^{2}+c^{2}}}}\right)\!,\end{cases}}t\in [0;2\pi ).

{\ displaystyle {\ begin {cases} x = x_ {0} + {\ dfrac {R} {\ sqrt {a ^ {2} + c ^ {2}}}} \ cdot \! \ left (c \ cdot \ cos t - {\ dfrac {a \ cdot b \ cdot \ sin t} {\ sqrt {a ^ {2} + b ^ {2} + c ^ {2}}} \ right) \!, \\ [10pt] y = y_ {0} + {\ dfrac {R \ cdot {\ sqrt {a ^ {2} + c ^ {2}}}} {\ sqrt {a ^ {2} + b ^ {2} + c ^ {2}}}} \ cdot \ sint, \\ [10pt] z = z_ {0} - {\ dfrac {R} {\ sqrt {a ^ {2} + c ^ {2}}} } \ cdot \! \ left (a \ cdot \ cos t + {\ dfrac {b \ cdot c \ cdot \ sin t} {\ sqrt {a ^ {2} + b ^ {2} + c ^ {2}} }} \ right) \!, \ end {cases}} t \ in [0; 2 \ pi).}

Tangents and normals

The equation of the tangent to a circle at a point $\left(x_{1},y_{1}\right)$ ${\ displaystyle \ left (x_ {1}, y_ {1} \ right)}$ defined by the equation

\left({\frac {A}{2}}+x_{1}\right)x+\left({\frac {B}{2}}+y_{1}\right)y+\left({\frac {A}{2}}x_{1}+{\frac {B}{2}}y_{1}+C\right)=0.

{\ displaystyle \ left ({\ frac {A} {2}} + x_ {1} \ right) x + \ left ({\ frac {B} {2}} + y_ {1} \ right) y + \ left ( {\ frac {A} {2}} x_ {1} + {\ frac {B} {2}} y_ {1} + C \ right) = 0.}

The normal equation at the same point can be written as

{\frac {x-x_{1}}{2x_{1}+A}}={\frac {y-y_{1}}{2y_{1}+B}}.

{\ displaystyle {\ frac {x-x_ {1}} {2x_ {1} + A}} = {\ frac {y-y_ {1}} {2y_ {1} + B}}.}

Concentric and orthogonal circles

Concentric circles

Circles with a common center, but with different radii, are called concentric . Two circles defined by the equations:

x^{2}+y^{2}+A_{1}x+B_{1}y+C_{1}=0,\;\;\;x^{2}+y^{2}+A_{2}x+B_{2}y+C_{2}=0

{\ displaystyle x ^ {2} + y ^ {2} + A_ {1} x + B_ {1} y + C_ {1} = 0, \; \; \; x ^ {2} + y ^ {2 } + A_ {2} x + B_ {2} y + C_ {2} = 0}

are concentric if and only if $A_{1}=A_{2}$ ${\ displaystyle A_ {1} = A_ {2}}$ and $B_{1}=B_{2}.$ ${\ displaystyle B_ {1} = B_ {2}.}$

Two circles are orthogonal (that is, intersecting at right angles ) if and only if the condition

A_{1}A_{2}+B_{1}B_{2}=2\left(C_{1}+C_{2}\right).

{\ displaystyle A_ {1} A_ {2} + B_ {1} B_ {2} = 2 \ left (C_ {1} + C_ {2} \ right).}

Additional Information

Defining triangles for one circle

A tangent to the circumscribed circle is drawn through the vertex of the triangle

A triangle ABC is called inscribed in a circle (A, B, C) if all three of its vertices A , B, and C lie on this circle. Moreover, the circle is called the circumscribed circle of the triangle ABC (see. Circumstances described ).
A tangent to a circle drawn through any vertex of the triangle inscribed in it is antiparallel to the side of the triangle opposite the given vertex.
A triangle ABC is called circumscribed around a circle (A ', B', C ') if all three of its sides AB , BC and CA are tangent to this circle at some points, respectively, C' , A ' and B' . Moreover, the circle is called the inscribed circle of the triangle ABC (See. Inscribed circle ).

Circle definition options

A circle of diameter AB is a figure consisting of points A, B and all points of the plane from which the segment AB is visible at right angles (Definition through an angle based on the diameter of the circle ).
A circle with the chord AB is a figure consisting of points A, B and all points of the plane from which the segment AB is visible at a constant angle on one side equal to the inscribed angle of the arc AB , and at another constant angle on the other side equal to 180 degrees minus the inscribed angle of the arc AB above (Definition through the inscribed angle ).
A figure consisting of such points $X,$ ${\ displaystyle X,}$ that the ratio of the lengths of the segments AX and BX is constant: ${\frac {AX}{BX}}=c\neq 1,$ ${\ displaystyle {\ frac {AX} {BX}} = c \ neq 1,}$ is a circle (Definition through the circle of Apollonius ).
A figure consisting of all such points, for each of which the sum of the squared distances to two given points is equal to a given value, greater than half the square of the distance between these points, is also a circle (Definition through the Pythagorean theorem for an arbitrary right-angled triangle inscribed in a circle with a hypotenuse which is the diameter of the circle).
A circle is a closed, self-disjoint figure with the following property. If any chords AB , CD , GF , etc., are drawn through an arbitrary point E inside it, then the equalities are true: $AE\cdot EB=CE\cdot ED=GE\cdot EF$ ${\ displaystyle AE \ cdot EB = CE \ cdot ED = GE \ cdot EF}$ (see fig.). Equalities will always be satisfied regardless of the choice of the point E and the directions of the chords drawn through it (Definition through intersecting chords).

AE\cdot EB=CE\cdot ED

{\ displaystyle AE \ cdot EB = CE \ cdot ED}

A circle is a closed, self-disjoint figure with the following property. If through an arbitrary point M outside it draw two tangents to the points of their tangency with the circle, for example, A and B , then their lengths will always be equal: $MA=MB$ ${\ displaystyle MA = MB}$ . Equality will always be satisfied regardless of the choice of the point M (Definition through equal tangents ).

A circle is a closed, self-disjoint figure with the following property. The ratio of the length of any of its chords to the sine of any of its inscribed angles , based on this chord, is a constant value equal to the diameter of this circle (Definition through the sine theorem ).
A circle is a special case of an ellipse in which the distance between the foci is zero (Definition through a degenerate ellipse ).
The circle is a sinusoidal spiral at $n=1$ ${\ displaystyle n = 1}$ .

Related definitions for two circles

Two circles having a common center are called concentric .
Two circles having only one common point are called tangent externally if their circles do not have other common points, and internally if their circles lie one inside the other.
Two circles having two common points are called intersecting . Their circles (limited by them) intersect in an area called a double circular segment.
The angle between two intersecting (or touching) circles is the angle between their tangents drawn at a common point of intersection (or tangency).
Also, the angle between two intersecting (or touching) circles can be considered the angle between their radii (diameters) drawn at a common point of intersection (or contact).
Since for any circle its radius (or diameter) and tangent drawn through any point of the circle are mutually perpendicular, the radius (or diameter) can be considered normal to the circle constructed at its given point. Therefore, the two types of angles defined in the two previous two paragraphs will always be equal to each other, like angles with mutually perpendicular sides.
Two circles intersecting at right angles are called orthogonal . Circles can be considered orthogonal if they form a right angle with each other.
The radical axis of two circles is the locus of points whose degrees with respect to two given circles are equal. In other words, the lengths of four tangents drawn to two given circles from any point M of a given locus of a point are equal.

Angle definitions for two circles

The angle between two intersecting circles is the angle between the tangents to the circles at the intersection of these circles. Both angles between two intersecting circles are equal.
The angle between two disjoint circles is the angle between two common tangents to two circles, formed at the intersection of these two tangents. The intersection point of these two tangents should lie between two circles, and not from the side of one of them (this angle is not considered). Both vertical angles between two disjoint circles are equal.

Orthogonality

Two circles intersecting at right angles are called orthogonal . Circles can be considered orthogonal if they form a right angle with each other.
Two circles intersecting at points A and B with centers O and O ' are called orthogonal if the angles OAO' and OBO ' are right. It is this condition that guarantees a right angle between the circles. In this case, the radii (normals) of two circles are perpendicular, drawn to the point of intersection. Consequently, the tangents of two circles drawn to the point of their intersection are also perpendicular. The tangent of the circle is perpendicular to the radius (normal) drawn to the point of tangency. Typically, the angle between the curves is the angle between their tangents drawn at the point of intersection.
Perhaps another additional condition. Let two circles intersecting at points A and B have midpoints of intersecting arcs at points C and D , that is, the arc AC is equal to the arc CB , the arc AD is equal to the arc DB . Then these circles are called orthogonal if the angles CAD and CBD are right.

Related definitions for three circles

Three circles are called mutually tangent (intersecting), if any two of them touch (suppress) each other.
In geometry, the radical center of three circles is the intersection point of the three radical axes of pairs of circles. If the radical center lies outside all three circles, then it is the center of a single circle ( radical circle ) that intersects the three given circles orthogonally .

Archimedes lemma

Lemma of Archimedes . If a circle is inscribed in a circle segment, contracted by a chord $B C$ ${\ displaystyle BC}$ and touches the arc at the point $A_{1}$ ${\ displaystyle A_ {1}}$ and the chords are at the point $A_{2}$ ${\ displaystyle A_ {2}}$ then direct $A_{1}A_{2}$ ${\ displaystyle A_ {1} A_ {2}}$ is the angle bisector $BA_{1}C$ ${\ displaystyle BA_ {1} C}$ . Archimedes' lemma plays an important role in constructing the isocircular transformation .

Evidence

Let be $G$ ${\ displaystyle G}$ - homothety transforming a small circle into a large one. Then it is clear that $A_{1}$ ${\ displaystyle A_ {1}}$ is the center of this homothety. Then direct $B C$ ${\ displaystyle BC}$ will go into some kind of direct $a$ ${\ displaystyle a}$ concerning a large circle, and $A_{2}$ ${\ displaystyle A_ {2}}$ will go to a point on this line and belonging to a large circle. Recalling that homothety translates lines into lines parallel to them, we understand that $a\parallel BC$ ${\ displaystyle a \ parallel BC}$ . Let be $G(A_{2})=A_{3}$ ${\ displaystyle G (A_ {2}) = A_ {3}}$ and $D$ ${\ displaystyle D}$ - point on the line $a$ ${\ displaystyle a}$ such that $\angle CA_{3}D$ ${\ displaystyle \ angle CA_ {3} D}$ - sharp, and $E$ ${\ displaystyle E}$ - such a point on the line $a$ ${\ displaystyle a}$ , what $\angle BA_{3}E$ ${\ displaystyle \ angle BA_ {3} E}$ - sharp. Then, since $a$ ${\ displaystyle a}$ - tangent to a large circle $\angle CA_{3}D$ ${\ displaystyle \ angle CA_ {3} D}$ $=$ ${\ displaystyle =}$ $\angle CBA_{3}$ ${\ displaystyle \ angle CBA_ {3}}$ $=\angle BA_{3}E=\angle BCA_{3}$ ${\ displaystyle = \ angle BA_ {3} E = \ angle BCA_ {3}}$ . Consequently $\bigtriangleup BCA_{3}$ ${\ displaystyle \ bigtriangleup BCA_ {3}}$ - isosceles, which means $\angle BA_{1}A_{3}=\angle CA_{1}A_{3}$ ${\ displaystyle \ angle BA_ {1} A_ {3} = \ angle CA_ {1} A_ {3}}$ , i.e $A_{1}A_{2}$ ${\ displaystyle A_ {1} A_ {2}}$ - angle bisector $\angle BA_{1}C$ ${\ displaystyle \ angle BA_ {1} C}$ .

Descartes' theorem for the radii of four pairwise tangent circles

Descartes' theorem states that the radii of any four mutually tangent circles satisfy some quadratic equation . They are sometimes called Soddy circles.

Multidimensional Generalization

A generalized circle can be defined for any mathematical structure where the concept of distance is given. In particular, a hypersphere is a generalization for multidimensional Euclidean space ; in three-dimensional space this is a common sphere . In spherical geometry, an important role is played by circles on a sphere whose center coincides with the center of the sphere (" big circles ").

Notes

↑ Mathematical Encyclopedia, 1984 , p. 15-16.
↑ Elementary mathematics, 1976 , p. 408-409.
↑ ¹ ² ³ Elementary Mathematics, 1976 , p. 410-411.
↑ Elementary mathematics, 1976 , p. 409-410.
↑ Elementary mathematics, 1976 , p. 510.

Literature

Atanasyan L. S. , Butuzov V. F. .. et al. Additional chapters to the textbook of grade 8 // Geometry. - 3rd edition. - M .: Vita-Press, 2003.
Zaitsev V.V., Ryzhkov V.V., Skanavi M.I. Elementary mathematics. Repeat course. - Third edition, stereotyped. - M .: Nauka, 1976 .-- 591 p.
Korn G., Korn T. Properties of circles, ellipses, hyperbolas and parabolas // Mathematics Handbook. - 4th edition. - M .: Nauka, 1978.- S. 70.
Markushevich A. I. Wonderful curves, issue 4 . - M .: Gostekhizdat, 1952. - 32 p. Archived on September 14, 2008. Archived September 14, 2008 on Wayback Machine
Circle // Mathematical Encyclopedia (in 5 volumes). - M .: Soviet Encyclopedia , 1984. - T. 4.

Links

Circumference at www.univer.omsk.su.
Circle and circle on the Metmat website (methodology of teaching mathematics).

[_3c5f123762fc9415-1] Mathematical Encyclopedia, 1984 , p. 15-16.

[_4e5a371faa606a2a-2] Elementary mathematics, 1976 , p. 408-409.

[EM410-3] ¹ ² ³ Elementary Mathematics, 1976 , p. 410-411.

[_b8dd3b53bf0f2ad1-4] Elementary mathematics, 1976 , p. 409-410.

[_01ee66deb896e74b-5] Elementary mathematics, 1976 , p. 510.