Logarithm

Binary Logarithm Graph

Logarithm of a number $b$ ${\ displaystyle b}$ $b$ on the basis of $a$ ${\ displaystyle a}$ $a$ (from other Greek. λόγος “word; relation” + ἀριθμός “number” ^[1] ) is defined ^[2] as an indicator of the degree to which the base should be raised $a$ ${\ displaystyle a}$ $a$ to get the number $b$ ${\ displaystyle b}$ $b$ . Designation: $\log _{a}b$ ${\ displaystyle \ log _ {a} b}$ $\ log _ {a} b$ , pronounced: " logarithm $b$ ${\ displaystyle b}$ $b$ on the basis of $a$ ${\ displaystyle a}$ $a$ ".

From the definition it follows that finding $x=\log _{a}b$ ${\ displaystyle x = \ log _ {a} b}$ ${\ displaystyle x = \ log _ {a} b}$ equivalent to solving the equation $a^{x}=b$ ${\ displaystyle a ^ {x} = b}$ $a ^ {x} = b$ . For example, $\log _{2}8=3$ ${\ displaystyle \ log _ {2} 8 = 3}$ $\ log _ {2} 8 = 3$ , because $2^{3}=8$ ${\ displaystyle 2 ^ {3} = 8}$ $2 ^ {3} = 8$ .

The calculation of the logarithm is called logarithm . The numbers $a, b$ ${\ displaystyle a, b}$ $a, b$ most often real , but there is also a theory of complex logarithms.

Logarithms have unique properties that determined their widespread use to significantly simplify time-consuming calculations ^[3] . During the transition “to the world of logarithms”, multiplication is replaced by a much simpler addition, division by subtraction, and exponentiation and root extraction are converted into multiplication and division by an exponent, respectively. Laplace said that the invention of logarithms, "reducing the work of an astronomer, doubled his life" ^[4] .

The definition of logarithms and a table of their values (for trigonometric functions ) was first published in 1614 by the Scottish mathematician John Napier . Logarithmic tables, expanded and refined by other mathematicians, were universally used for scientific and engineering calculations for more than three centuries, until electronic calculators and computers appeared.

Over time, it turned out that the logarithmic function $y=\log _{a}x$ ${\ displaystyle y = \ log _ {a} x}$ $y = \ log _ {a} x$ It is indispensable in many other areas of human activity: solving differential equations , classifying values of quantities (for example, frequency and intensity of sound ), approximating various dependencies, information theory, probability theory , etc. This function is one of the elementary ones , it is inverse with respect to to exponential function . Most commonly used real logarithms with bases $2$ ${\ displaystyle 2}$ $2$ ( binary ) $e$ ${\ displaystyle e}$ $e$ ( natural logarithm ) and $ten$ ${\ displaystyle 10}$ $ten$ ( decimal ).

Real Logarithm

Logarithm of a real number $x=\log _{a}b$ ${\ displaystyle x = \ log _ {a} b}$ $x=\log _{a}b$ by definition, there is a solution to the equation $a^{x}=b$ ${\ displaystyle a ^ {x} = b}$ $a^{x}=b$ . Happening $a=1$ ${\ displaystyle a = 1}$ $a=1$ is not of interest, since then at $b\neq 1$ ${\ displaystyle b \ neq 1}$ $b\neq 1$ this equation has no solution, but for $b=1$ ${\ displaystyle b = 1}$ $b=1$ any number is a solution; in both cases the logarithm is not defined. Similarly, we conclude that the logarithm does not exist for zero or negative $a$ ${\ displaystyle a}$ $a$ ; in addition, the value of the exponential function $a^{x}$ ${\ displaystyle a ^ {x}}$ $a^{x}$ always positive, therefore the case of negative should also be excluded $b$ ${\ displaystyle b}$ $b$ . Finally we get ^[5] :

Real Logarithm $\log _{a}b$ ${\ displaystyle \ log _ {a} b}$ makes sense when $a>0,a\neq 1,b>0$ ${\ displaystyle a> 0, a \ neq 1, b> 0}$

As is known, the exponential function $y=a^{x}$ ${\ displaystyle y = a ^ {x}}$ (when these conditions are met for $a$ ${\ displaystyle a}$ ) exists, is monotonous and takes each value only once, and the range of its values contains all positive real numbers ^[6] . It follows that the value of the real logarithm of a positive number always exists and is uniquely determined.

The most widely used are the following types of logarithms:

Natural : $\log _{e}\,b$ ${\ displaystyle \ log _ {e} \, b}$ or $\ln \,b$ ${\ displaystyle \ ln \, b}$ base: Euler number ( $e$ ${\ displaystyle e}$ );
Decimal : $\log _{10}\,b$ ${\ displaystyle \ log _ {10} \, b}$ or $\lg \,b$ ${\ displaystyle \ lg \, b}$ base: number $ten$ ${\ displaystyle 10}$ ;
Binary : $\log _{2}\,b$ ${\ displaystyle \ log _ {2} \, b}$ or $\operatorname {lb} \,b$ ${\ displaystyle \ operatorname {lb} \, b}$ base: $2$ ${\ displaystyle 2}$ . They are used, for example, in information theory , computer science , in many sections of discrete mathematics .

Properties

Basic Logarithmic Identity

From the definition of the logarithm follows the main logarithmic identity ^[7] :

a^{\log _{a}b}=b

{\ displaystyle a ^ {\ log _ {a} b} = b}

Corollary: the equality of two real logarithms implies the equality of logarithm expressions. In fact, if $\log _{a}b=\log _{a}c$ ${\ displaystyle \ log _ {a} b = \ log _ {a} c}$ then $a^{\log _{a}b}=a^{\log _{a}c}$ ${\ displaystyle a ^ {\ log _ {a} b} = a ^ {\ log _ {a} c}}$ , where, according to the basic identity: $b=c$ ${\ displaystyle b = c}$ .

Logarithms of Unit and Number Equal to the Base

Two equalities obvious from the definition of the logarithm:

\log _{a}1=0;\;\log _{a}a=1.

{\ displaystyle \ log _ {a} 1 = 0; \; \ log _ {a} a = 1.}

Logarithm of a product quotient from division, degree and root

Here is a summary of the formulas under the assumption that all values are positive ^[8] :

	Formula	Example
Composition	$\log _{a}(xy)=\log _{a}(x)+\log _{a}(y)$ ${\ displaystyle \ log _ {a} (xy) = \ log _ {a} (x) + \ log _ {a} (y)}$	$\log _{3}(243)=\log _{3}(9\cdot 27)=\log _{3}(9)+\log _{3}(27)=2+3=5$ ${\ displaystyle \ log _ {3} (243) = \ log _ {3} (9 \ cdot 27) = \ log _ {3} (9) + \ log _ {3} (27) = 2 + 3 = five}$
Quotient from division	$\log _{a}\!\left({\frac {x}{y}}\right)=\log _{a}(x)-\log _{a}(y)$ ${\ displaystyle \ log _ {a} \! \ left ({\ frac {x} {y}} \ right) = \ log _ {a} (x) - \ log _ {a} (y)}$	$\lg \left({\frac {1}{1000}}\right)=\lg(1)-\lg(1000)=0-3=-3$ ${\ displaystyle \ lg \ left ({\ frac {1} {1000}} \ right) = \ lg (1) - \ lg (1000) = 0-3 = -3}$
Power	$\log _{a}(x^{p})=p\log _{a}(x)$ ${\ displaystyle \ log _ {a} (x ^ {p}) = p \ log _ {a} (x)}$	$\log _{2}(64)=\log _{2}(2^{6})=6\log _{2}(2)=6$ ${\ displaystyle \ log _ {2} (64) = \ log _ {2} (2 ^ {6}) = 6 \ log _ {2} (2) = 6}$
Root	$\log _{a}{\sqrt[{p}]{x}}={\frac {\log _{a}(x)}{p}}$ ${\ displaystyle \ log _ {a} {\ sqrt [{p}] {x}} = {\ frac {\ log _ {a} (x)} {p}}}$	$\lg {\sqrt {1000}}={\frac {1}{2}}\lg 1000={\frac {3}{2}}=1.5$ ${\ displaystyle \ lg {\ sqrt {1000}} = {\ frac {1} {2}} \ lg 1000 = {\ frac {3} {2}} = 1.5}$

There is an obvious generalization of the given formulas to the case when negative values of variables are allowed, for example:

\log _{a}|xy|=\log _{a}|x|+\log _{a}|y|

{\ displaystyle \ log _ {a} | xy | = \ log _ {a} | x | + \ log _ {a} | y |}

\log _{a}\!\left|{\frac {x}{y}}\right|=\log _{a}|x|-\log _{a}|y|

{\ displaystyle \ log _ {a} \! \ left | {\ frac {x} {y}} \ right | = \ log _ {a} | x | - \ log _ {a} | y |}

Formulas for the logarithm of a product can be easily generalized to an arbitrary number of factors:

\log _{a}(x_{1}x_{2}\dots x_{n})=\log _{a}(x_{1})+\log _{a}(x_{2})+\dots +\log _{a}(x_{n})

{\ displaystyle \ log _ {a} (x_ {1} x_ {2} \ dots x_ {n}) = \ log _ {a} (x_ {1}) + \ log _ {a} (x_ {2} ) + \ dots + \ log _ {a} (x_ {n})}

\log _{a}|x_{1}x_{2}\dots x_{n}|=\log _{a}|x_{1}|+\log _{a}|x_{2}|+\dots +\log _{a}|x_{n}|

{\ displaystyle \ log _ {a} | x_ {1} x_ {2} \ dots x_ {n} | = \ log _ {a} | x_ {1} | + \ log _ {a} | x_ {2} | + \ dots + \ log _ {a} | x_ {n} |}

The above properties explain why the use of logarithms (before the invention of calculators) greatly facilitated the calculation. For example, multiplication of multi-digit numbers $x, y$ ${\ displaystyle x, y}$ using logarithmic tables performed according to the following algorithm:

find the logarithms of numbers in tables $x, y$ ${\ displaystyle x, y}$ ;
add up these logarithms, getting (according to the first property) the logarithm of the product $x\cdot y$ ${\ displaystyle x \ cdot y}$ ;
by the logarithm of the product, find the product in the tables.

Division, which without the help of logarithms is much more laborious than multiplication, was performed according to the same algorithm, only with the addition of addition of logarithms to subtraction. Similarly simplified exponentiation and root extraction .

Replacing the base of a logarithm

Logarithm $\log _{a}b$ ${\ displaystyle \ log _ {a} b}$ on the basis of $a$ ${\ displaystyle a}$ can be converted ^[5] to a logarithm on a different basis $c$ ${\ displaystyle c}$ :

\log _{a}b={\frac {\log _{c}b}{\log _{c}a}}

{\ displaystyle \ log _ {a} b = {\ frac {\ log _ {c} b} {\ log _ {c} a}}}

Corollary (with $b=c$ ${\ displaystyle b = c}$ ) - permutation of the base and the logarithm expression:

\log _{a}b={\frac {1}{\log _{b}a}}

{\ displaystyle \ log _ {a} b = {\ frac {1} {\ log _ {b} a}}}

See an example of such a permutation in the decimal logarithm section.

Coefficient ${\frac {1}{\log _{c}a}}=\log _{a}c$ ${\ displaystyle {\ frac {1} {\ log _ {c} a}} = \ log _ {a} c}$ in the base replacement formula is called the module of the transition from one base to another ^[9] .

Inequalities

Logarithm value $\log _{a}{b}$ ${\ displaystyle \ log _ {a} {b}}$ positive if and only if the numbers $a, b$ ${\ displaystyle a, b}$ lie on one side of the unit (that is, either both are larger than one, or both are smaller). If $a, b$ ${\ displaystyle a, b}$ lie on opposite sides of unity, then the logarithm is negative ^[10] .

Any inequality for positive numbers can be logarithmed. Moreover, if the base of the logarithm is greater than unity, then the inequality sign is preserved, and if the base is less than unity, the inequality sign is reversed ^[10] .

Other identities and properties

If the expressions for the base of the logarithm and for the logarithmic expression contain exponentiation, for simplification, the following identity can be applied:

{\log _{a^{q}}{b}}^{p}={\frac {p}{q}}\log _{a}{b}

{\ displaystyle {\ log _ {a ^ {q}} {b}} ^ {p} = {\ frac {p} {q}} \ log _ {a} {b}}

This identity is immediately obtained if the base is replaced in the logarithm on the left $a^{q}$ ${\ displaystyle a ^ {q}}$ on $a$ ${\ displaystyle a}$ according to the above formula for replacing the base. The consequences:

\log _{a^{k}}b={\frac {1}{k}}\log _{a}b;\quad \log _{\sqrt[{n}]{a}}b=n\log _{a}b;\quad \log _{a^{k}}b^{k}=\log _{a}b

{\ displaystyle \ log _ {a ^ {k}} b = {\ frac {1} {k}} \ log _ {a} b; \ quad \ log _ {\ sqrt [{n}] {a}} b = n \ log _ {a} b; \ quad \ log _ {a ^ {k}} b ^ {k} = \ log _ {a} b}

Another useful identity:

c^{\log _{a}b}=b^{\log _{a}c}

{\ displaystyle c ^ {\ log _ {a} b} = b ^ {\ log _ {a} c}}

To prove it, we note that the logarithms of the left and right sides are base $a$ ${\ displaystyle a}$ match (equal $\log _{a}b\cdot \log _{a}c$ ${\ displaystyle \ log _ {a} b \ cdot \ log _ {a} c}$ ), and then, according to the corollary of the main logarithmic identity, the left and right sides are identically equal. Prologarithm the previous identity on an arbitrary basis $d,$ ${\ displaystyle d,}$ we get one more identity "exchange of grounds":

\log _{a}b\cdot \log _{d}c=\log _{d}b\cdot \log _{a}c

{\ displaystyle \ log _ {a} b \ cdot \ log _ {d} c = \ log _ {d} b \ cdot \ log _ {a} c}

Logarithmic function

Graphs of logarithmic functions

Logarithmic function is inverse to exponential

Key Features

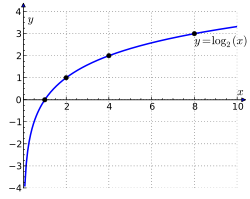
If we consider the logarithm number as a variable, we get the logarithmic function $y=\log _{a}x$ ${\ displaystyle y = \ log _ {a} x}$ . It is defined at $a>0;\ a\neq 1;x>0$ ${\ displaystyle a> 0; \ a \ neq 1; x> 0}$ . Value Range: $E(y)=(-\infty ;+\infty )$ ${\ displaystyle E (y) = (- \ infty; + \ infty)}$ . This curve is often called the logarithmic ^[11] . From the formula for replacing the base of the logarithm, it can be seen that the graphs of logarithmic functions with different bases larger than unity differ from each other only in scale along the axis $y$ ${\ displaystyle y}$ ; the graphs for bases smaller than one are their mirror image relative to the horizontal axis.

From the definition it follows that the logarithmic dependence is the inverse function for the exponential function $y=a^{x}$ ${\ displaystyle y = a ^ {x}}$ , therefore, their graphs are symmetrical with respect to the bisector of the first and third quadrants (see figure). Like the exponential, the logarithmic function belongs to the category of transcendental functions .

The function is strictly increasing for $a>1$ ${\ displaystyle a> 1}$ (see graphs below) and strictly decreasing at $0<a<1$ ${\ displaystyle 0 <a <1}$ . The graph of any logarithmic function passes through a point $(1;0)$ ${\ displaystyle (1; 0)}$ . The function is continuous and infinitely differentiable everywhere in its domain of definition.

Ordinate axis ( $x=0$ ${\ displaystyle x = 0}$ ) is a vertical asymptote , because:

\lim _{x\to 0+0}\log _{a}x=-\infty

{\ displaystyle \ lim _ {x \ to 0 + 0} \ log _ {a} x = - \ infty}

at

a>1

{\ displaystyle a> 1}

;

\lim _{x\to 0+0}\log _{a}x=+\infty

{\ displaystyle \ lim _ {x \ to 0 + 0} \ log _ {a} x = + \ infty}

at

0<a<1

{\ displaystyle 0 <a <1}

.

The derivative of the logarithmic function is equal to:

{\frac {d}{dx}}\log _{a}x={\frac {1}{x\cdot \ln a}}

{\ displaystyle {\ frac {d} {dx}} \ log _ {a} x = {\ frac {1} {x \ cdot \ ln a}}}

From the point of view of algebra, the logarithmic function implements the (only possible) isomorphism of the multiplicative group of positive real numbers and the additive group of all real numbers. In other words, the logarithmic function is the only (defined for all positive values of the argument) continuous solution of the functional equation ^[12] :

f(xy)=f(x)+f(y)

{\ displaystyle f (xy) = f (x) + f (y)}

Natural Logarithm

From the above general formula of the derivative for the natural logarithm, we obtain a particularly simple result:

{\frac {d}{dx}}\ln x={\frac {1}{x}}

{\ displaystyle {\ frac {d} {dx}} \ ln x = {\ frac {1} {x}}}

For this reason, it is natural logarithms that are mainly used in mathematical research. They often appear when solving differential equations , studying statistical dependencies (for example, the distribution of primes ), etc.

The natural logarithm is equal to the area under the hyperbola

Integrating the formula for the derivative in the range from $x=1$ ${\ displaystyle x = 1}$ before $x=b$ ${\ displaystyle x = b}$ , we get:

\ln b=\int \limits _{1}^{b}{\frac {dx}{x}}

{\ displaystyle \ ln b = \ int \ limits _ {1} ^ {b} {\ frac {dx} {x}}}

In other words, the natural logarithm is equal to the area under the hyperbola $y={\frac {1}{x}}$ ${\ displaystyle y = {\ frac {1} {x}}}$ for the specified interval x .

The indefinite integral of the natural logarithm is easy to find by integration by parts :

\int {\ln x\,\mathrm {d} x}=x\ln x-x+C

{\ displaystyle \ int {\ ln x \, \ mathrm {d} x} = x \ ln x-x + C}

In mathematical analysis and the theory of differential equations , the concept of a logarithmic derivative of a function plays a large role $f(x)$ ${\ displaystyle f (x)}$ :

{\frac {d}{dx}}\ln(f(x))={\frac {f'(x)}{f(x)}}

{\ displaystyle {\ frac {d} {dx}} \ ln (f (x)) = {\ frac {f '(x)} {f (x)}}}

Series expansion and calculation of the natural logarithm

We expand the natural logarithm in a Taylor series near unity:

\ln(1+x)=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-{\frac {x^{4}}{4}}+\dots

{\ displaystyle \ ln (1 + x) = x - {\ frac {x ^ {2}} {2}} + {\ frac {x ^ {3}} {3}} - {\ frac {x ^ { 4}} {4}} + \ dots}

(Row 1)

This series, called the " Mercator series," converges at $-1<x\leqslant 1$ ${\ displaystyle -1 <x \ leqslant 1}$ . In particular:

\ln 2=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+\dots

{\ displaystyle \ ln 2 = 1 - {\ frac {1} {2}} + {\ frac {1} {3}} - {\ frac {1} {4}} + \ dots}

The formula of row 1 is unsuitable for the practical calculation of logarithms due to the fact that the series converges very slowly and only in a narrow interval. However, it is easy to obtain from it a more convenient formula:

\ln \left({\frac {1+x}{1-x}}\right)=2\left(x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}+{\frac {x^{7}}{7}}+\dots \right)

{\ displaystyle \ ln \ left ({\ frac {1 + x} {1-x}} \ right) = 2 \ left (x + {\ frac {x ^ {3}} {3}} + {\ frac { x ^ {5}} {5}} + {\ frac {x ^ {7}} {7}} + \ dots \ right)}

(Row 2)

This series converges faster, and in addition, the left side of the formula can now express the logarithm of any positive number. This algorithm is already suitable for real numerical calculations of the values of logarithms, but it is not the best from the point of view of complexity. There are more efficient algorithms ^[13] .

Decimal Logarithm

Base 10 logarithms (symbol: $\lg x$ ${\ displaystyle \ lg x}$ ) Before the invention of calculators , they were widely used for calculations. They have an advantage over logarithms with a different basis: the whole part $[\lg x]$ ${\ displaystyle [\ lg x]}$ logarithm of a number $x$ ${\ displaystyle x}$ easy to determine ^[14] :

If a $x\geqslant 1$ ${\ displaystyle x \ geqslant 1}$ then $[\lg x]$ ${\ displaystyle [\ lg x]}$ 1 less than the number of digits in the integer part of the number $x$ ${\ displaystyle x}$ . For example, it’s immediately obvious that $\lg 345$ ${\ displaystyle \ lg 345}$ is in between $(2,3)$ ${\ displaystyle (2,3)}$ .
If a $0<x<1$ ${\ displaystyle 0 <x <1}$ then closest to $\lg x$ ${\ displaystyle \ lg x}$ the integer down is equal to the total number of zeros in $x$ ${\ displaystyle x}$ before the first non-zero digit (including zero before the comma), taken with a minus sign. For example, $\lg 0{,}0014$ ${\ displaystyle \ lg 0 {,} 0014}$ is in the range $(-3,-2)$ ${\ displaystyle (-3, -2)}$ .

In addition, when transferring the decimal point in a number to $n$ ${\ displaystyle n}$ digits, the decimal logarithm of this number changes to $n$ ${\ displaystyle n}$ . For example, $\lg 8314{,}63=\lg 8{,}31463+3$ ${\ displaystyle \ lg 8314 {,} 63 = \ lg 8 {,} 31463 + 3}$ . It follows that to calculate the decimal logarithms, it is enough to compile a table of logarithms for numbers in the range from $one$ ${\ displaystyle 1}$ before $ten$ ${\ displaystyle 10}$ ^[14] .

Relationship with the natural logarithm ^[15] :

\ln x\approx 2{,}30259\ \lg x,\quad \ln x={\frac {\lg x}{\lg e}}=\ln 10\cdot \lg x=(2{,}30259\dots )\lg x

{\ displaystyle \ ln x \ approx 2 {,} 30259 \ \ lg x, \ quad \ ln x = {\ frac {\ lg x} {\ lg e}} = \ ln 10 \ cdot \ lg x = (2 {,} 30259 \ dots) \ lg x}

\lg x\approx 0{,}43429\ \ln x,\quad \lg x={\frac {\ln x}{\ln 10}}=\lg e\cdot \ln x=(0{,}43429\dots )\ln x

{\ displaystyle \ lg x \ approx 0 {,} 43429 \ \ ln x, \ quad \ lg x = {\ frac {\ ln x} {\ ln 10}} = \ lg e \ cdot \ ln x = (0 {,} 43429 \ dots) \ ln x}

Since the use of logarithms for calculations with the advent of computer technology has almost ceased, today the decimal logarithm is largely replaced by the natural one ^[16] . It is preserved mainly in those mathematical models where it is historically rooted - for example, when constructing logarithmic scales .

Limit ratios

Here are a few useful limits related to logarithms ^[17] :

\lim _{x\to 0}{\frac {\log _{a}(1+x)}{x}}=\log _{a}e={\frac {1}{\ln a}}

{\ displaystyle \ lim _ {x \ to 0} {\ frac {\ log _ {a} (1 + x)} {x}} = \ log _ {a} e = {\ frac {1} {\ ln a}}}

\lim _{x\to 0^{+}}x^{b}\log _{a}x=0\quad (b>0)

{\ displaystyle \ lim _ {x \ to 0 ^ {+}} x ^ {b} \ log _ {a} x = 0 \ quad (b> 0)}

\lim _{x\to \infty }{\frac {\log _{a}x}{x^{b}}}=0\quad (b>0)

{\ displaystyle \ lim _ {x \ to \ infty} {\ frac {\ log _ {a} x} {x ^ {b}}} = 0 \ quad (b> 0)}

\ln x=\lim _{n\to \infty }n\left({\sqrt[{n}]{x}}-1\right)=\lim _{n\to \infty }n\left(1-{\frac {1}{\sqrt[{n}]{x}}}\right)

{\ displaystyle \ ln x = \ lim _ {n \ to \ infty} n \ left ({\ sqrt [{n}] {x}} - 1 \ right) = \ lim _ {n \ to \ infty} n \ left (1 - {\ frac {1} {\ sqrt [{n}] {x}}} \ right)}

\ln x=\lim _{h\to 0}{\frac {x^{h}-1}{h}}

{\ displaystyle \ ln x = \ lim _ {h \ to 0} {\ frac {x ^ {h} -1} {h}}}

Other properties

From the Gelfond theorem it follows that if $a, b$ ${\ displaystyle a, b}$ - algebraic numbers ( $a\neq 1$ ${\ displaystyle a \ neq 1}$ ) then $\log _{a}b$ ${\ displaystyle \ log _ {a} b}$ либо рационален , либо трансцендентен . При этом логарифм рационален и равен $p \over q$ $p \over q$ только в том случае ^[18] , когда числа $a, b$ ${\displaystyle a,b}$ связаны соотношением $a^{p}=b^{q}$ $a^{p}=b^{q}$ .
Amount $\sum _{k=1}^{n}{\frac {1}{k}}$ $\sum _{k=1}^{n}{\frac {1}{k}}$ (частичная сумма гармонического ряда ) при больших $n$ ${\ displaystyle n}$ ведёт себя как $\ln n+\gamma +O(n^{-1})$ $\ln n+\gamma +O(n^{-1})$ where $\gamma \approx 0{,}5772156649\dots$ $\gamma \approx 0{,}5772156649\dots$ — постоянная Эйлера — Маскерони .

Комплексный логарифм

Определение и свойства

Для комплексных чисел логарифм определяется так же, как вещественный. На практике используется почти исключительно натуральный комплексный логарифм, который обозначается $\mathrm {Ln} \,z$ $\mathrm {Ln} \,z$ и определяется как решение $w$ ${\ displaystyle w}$ уравнения $e^{w}=z$ $e^{w}=z$ (другие, эквивалентные данному, варианты определения приведены ниже).

В поле комплексных чисел решение этого уравнения, в отличие от вещественного случая, не определено однозначно. Например, согласно тождеству Эйлера , $e^{\pi i}=-1$ $e^{\pi i}=-1$ ; однако также $e^{-\pi i}=e^{3\pi i}=e^{5\pi i}\dots =-1$ $e^{-\pi i}=e^{3\pi i}=e^{5\pi i}\dots =-1$ . Это связано с тем, что показательная функция вдоль мнимой оси является периодической (с периодом $2\pi i$ $2\pi i$ ) ^[19] , и одно и то же значение функция принимает бесконечно много раз. Таким образом, комплексная логарифмическая функция $w=\mathrm {Ln} \,z$ $w=\mathrm {Ln} \,z$ является многозначной .

Комплексный нуль не имеет логарифма, поскольку комплексная экспонента не принимает нулевого значения. Ненулевое $z$ ${\ displaystyle z}$ можно представить в показательной форме:

z=r\cdot e^{i\varphi }

z=r\cdot e^{i\varphi }

Then $\mathrm {Ln} \,z$ $\mathrm {Ln} \,z$ находится по формуле ^[20] :

\mathrm {Ln} \,z=\ln r+i\left(\varphi +2\pi k\right)

\mathrm {Ln} \,z=\ln r+i\left(\varphi +2\pi k\right)

Here $\ln \,r=\ln \,|z|$ $\ln \,r=\ln \,|z|$ — вещественный логарифм, $k$ ${\ displaystyle k}$ — произвольное целое число . Отсюда вытекает:

Комплексный логарифм $\mathrm {Ln} \,z$ $\mathrm {Ln} \,z$ существует для любого $z\neq 0$ $z\neq 0$ , и его вещественная часть определяется однозначно, в то время как мнимая часть имеет бесконечное множество значений, различающихся на целое кратное $2\pi$ {\ displaystyle 2 \ pi} .

The real part of the complex logarithm

The formula shows that for one and only one of the values the imaginary part is in the range $(-\pi ,\pi ]$ ${\ displaystyle (- \ pi, \ pi]}$ . This value is called the main value of the complex natural logarithm ^[11] . The corresponding (already unique) function is called the main branch of the logarithm and is denoted $\ln \,z$ ${\ displaystyle \ ln \, z}$ . Sometimes through $\ln \,z$ ${\ displaystyle \ ln \, z}$ also denote the value of the logarithm not lying on the main branch. If a $z$ ${\ displaystyle z}$ Is a real number, then the main value of its logarithm coincides with the usual real logarithm.

From the above formula it also follows that the real part of the logarithm is determined as follows through the components of the argument:

\operatorname {Re} (\ln(x+iy))={\frac {1}{2}}\ln(x^{2}+y^{2})

{\ displaystyle \ operatorname {Re} (\ ln (x + iy)) = {\ frac {1} {2}} \ ln (x ^ {2} + y ^ {2})}

The figure shows that the material part as a function of components is centrally symmetric and depends only on the distance to the origin. It is obtained by rotating the graph of the material logarithm around a vertical axis. With approaching zero, the function tends to $-\infty$ ${\ displaystyle - \ infty}$ .

The logarithm of a negative number is found by the formula ^[20] :

\mathrm {Ln} (-x)=\ln x+i\pi (2k+1)\qquad (x>0,\ k=0,\pm 1,\pm 2\dots )

{\ displaystyle \ mathrm {Ln} (-x) = \ ln x + i \ pi (2k + 1) \ qquad (x> 0, \ k = 0, \ pm 1, \ pm 2 \ dots)}

Examples of complex logarithm values

We give the main value of the logarithm ( $\ln$ ${\ displaystyle \ ln}$ ) and its general expression ( $\mathrm {Ln}$ ${\ displaystyle \ mathrm {Ln}}$ ) for some arguments:

\ln(1)=0;\;\mathrm {Ln} (1)=2k\pi i

{\ displaystyle \ ln (1) = 0; \; \ mathrm {Ln} (1) = 2k \ pi i}

\ln(-1)=i\pi ;\;\mathrm {Ln} (-1)=(2k+1)i\pi

{\ displaystyle \ ln (-1) = i \ pi; \; \ mathrm {Ln} (-1) = (2k + 1) i \ pi}

\ln(i)=i{\frac {\pi }{2}};\;\mathrm {Ln} (i)=i{\frac {4k+1}{2}}\pi

{\ displaystyle \ ln (i) = i {\ frac {\ pi} {2}}; \; \ mathrm {Ln} (i) = i {\ frac {4k + 1} {2}} \ pi}

One should be careful when transforming complex logarithms, taking into account that they are multi-valued, and therefore the equality of the logarithms of any expressions does not imply the equality of these expressions. An example of erroneous reasoning:

i\pi =\ln(-1)=\ln((-i)^{2})=2\ln(-i)=2(-i\pi /2)=-i\pi

{\ displaystyle i \ pi = \ ln (-1) = \ ln ((- i) ^ {2}) = 2 \ ln (-i) = 2 (-i \ pi / 2) = - i \ pi}

- an error which, however, indirectly indicates that values differing by $2i\pi$ ${\ displaystyle 2i \ pi}$ are the logarithms of the same number. Note that on the left is the main value of the logarithm, and on the right is the value from the underlying branch ( $k=-1$ ${\ displaystyle k = -1}$ ) The cause of the error is careless use of the property. $\log _{a}{(b^{p})}=p~\log _{a}b$ ${\ displaystyle \ log _ {a} {(b ^ {p})} = p ~ \ log _ {a} b}$ , which, generally speaking, implies in the complex case the entire infinite set of values of the logarithm, and not just the main value.

Complex logarithmic function and Riemann surface

Complex logarithm (imaginary part)

In complex analysis, instead of considering multi-valued functions on the complex plane, a different decision was made: to consider the function as unique, but not defined on the plane, but on a more complex manifold called the Riemann surface ^[21] . The complex logarithmic function also belongs to this category: its image (see the figure) consists of an infinite number of branches twisted in a spiral. This surface is continuous and simply connected . The only zero of the function (first order) is obtained for $z=1$ ${\ displaystyle z = 1}$ . Special Points: $z=0$ ${\ displaystyle z = 0}$ and $z=\infty$ ${\ displaystyle z = \ infty}$ (branch points of infinite order) ^[22] .

Due to the simply connected nature, the Riemann surface of the logarithm is a universal covering ^[23] for a complex plane without a point $0$ ${\ displaystyle 0}$ .

Analytical Continuation

The logarithm of a complex number can also be defined as the analytic continuation of the real logarithm to the entire complex plane . Let the curve $\Gamma$ ${\ displaystyle \ Gamma}$ starts at unity, does not go through zero and does not cross the negative part of the real axis. Then the main value of the logarithm at the end point $w$ ${\ displaystyle w}$ crooked $\Gamma$ ${\ displaystyle \ Gamma}$ can be determined by the formula ^[22] :

\ln w=\int \limits _{\Gamma }{du \over u}

{\ displaystyle \ ln w = \ int \ limits _ {\ Gamma} {du \ over u}}

If a $\Gamma$ ${\ displaystyle \ Gamma}$ Is a simple curve (without self-intersections), then for the numbers lying on it, logarithmic identities can be used without fear, for example:

\ln(wz)=\ln w+\ln z,~\forall z,w\in \Gamma \colon zw\in \Gamma

{\ displaystyle \ ln (wz) = \ ln w + \ ln z, ~ \ forall z, w \ in \ Gamma \ colon zw \ in \ Gamma}

The main branch of the logarithmic function is continuous and differentiable on the entire complex plane , except for the negative part of the real axis, on which the imaginary part changes abruptly to $2\pi$ ${\ displaystyle 2 \ pi}$ . But this fact is a consequence of the artificial limitation of the imaginary part of the main value by the interval $(-\pi ,\pi ]$ ${\ displaystyle (- \ pi, \ pi]}$ . If we consider all the branches of the function, then continuity takes place at all points except zero, where the function is not defined. If you allow the curve $\Gamma$ ${\ displaystyle \ Gamma}$ to cross the negative part of the real axis, then the first such intersection transfers the result from the branch of the main value to the neighboring branch, and each subsequent intersection causes a similar shift along the branches of the logarithmic function ^[22] (see figure).

From the analytical continuation formula it follows that on any branch of the logarithm ^[19] :

{\frac {d}{dz}}\ln z={1 \over z}

{\ displaystyle {\ frac {d} {dz}} \ ln z = {1 \ over z}}

For any circle $S$ ${\ displaystyle S}$ covering point $0$ ${\ displaystyle 0}$ :

\oint \limits _{S}{dz \over z}=2\pi i

{\ displaystyle \ oint \ limits _ {S} {dz \ over z} = 2 \ pi i}

The integral is taken in a positive direction ( counterclockwise ). This identity underlies the theory of residues .

You can also determine the analytic continuation of the complex logarithm using the above series: row 1 or row 2 , generalized to the case of a complex argument. However, from the form of these series it follows that in the unit the sum of the series is equal to zero, that is, the series refers only to the main branch of the multivalued function of the complex logarithm. The radius of convergence of both series is 1.

Relationship with inverse trigonometric and hyperbolic functions

Since complex trigonometric functions are associated with an exponential ( Euler formula ), the complex logarithm as an inverse of the exponential function is associated with inverse trigonometric functions ^[24] ^[25] :

\operatorname {Arcsin} z=-i\operatorname {Ln} (iz+{\sqrt {1-z^{2}}})

{\ displaystyle \ operatorname {Arcsin} z = -i \ operatorname {Ln} (iz + {\ sqrt {1-z ^ {2}}})}

\operatorname {Arccos} z=-i\operatorname {Ln} (z+i{\sqrt {1-z^{2}}})

{\ displaystyle \ operatorname {Arccos} z = -i \ operatorname {Ln} (z + i {\ sqrt {1-z ^ {2}}})}

\operatorname {Arctg} z=-{\frac {i}{2}}\ln {\frac {1+zi}{1-zi}}+k\pi \;(z\neq \pm i)

{\ displaystyle \ operatorname {Arctg} z = - {\ frac {i} {2}} \ ln {\ frac {1 + zi} {1-zi}} + k \ pi \; (z \ neq \ pm i )}

\operatorname {Arcctg} z=-{\frac {i}{2}}\ln {\frac {zi-1}{zi+1}}+k\pi \;(z\neq \pm i)

{\ displaystyle \ operatorname {Arcctg} z = - {\ frac {i} {2}} \ ln {\ frac {zi-1} {zi + 1}} + k \ pi \; (z \ neq \ pm i )}

Hyperbolic functions on the complex plane can be considered as trigonometric functions of an imaginary argument, and therefore there is a connection with the logarithm ^[25] :

\operatorname {Arsh} z=\operatorname {Ln} (z+{\sqrt {z^{2}+1}})

{\ displaystyle \ operatorname {Arsh} z = \ operatorname {Ln} (z + {\ sqrt {z ^ {2} +1}})}

- inverse hyperbolic sine

\operatorname {Arch} z=\operatorname {Ln} \left(z+{\sqrt {z^{2}-1}}\right)

{\ displaystyle \ operatorname {Arch} z = \ operatorname {Ln} \ left (z + {\ sqrt {z ^ {2} -1}} \ right)}

- inverse hyperbolic cosine

\operatorname {Arth} z={\frac {1}{2}}\operatorname {Ln} \left({\frac {1+z}{1-z}}\right)

{\ displaystyle \ operatorname {Arth} z = {\ frac {1} {2}} \ operatorname {Ln} \ left ({\ frac {1 + z} {1-z}} \ right)}

- inverse hyperbolic tangent

\operatorname {Arcth} z={\frac {1}{2}}\operatorname {Ln} \left({\frac {z+1}{z-1}}\right)

{\ displaystyle \ operatorname {Arcth} z = {\ frac {1} {2}} \ operatorname {Ln} \ left ({\ frac {z + 1} {z-1}} \ right)}

- inverse hyperbolic cotangent

Historical Review

Predecessors

The ideological source and stimulus for the use of logarithms was the fact (known even to Archimedes ^[26] ) that when multiplying degrees their indicators add up ^[27] : $a^{b}\cdot a^{c}=a^{b+c}$ ${\ displaystyle a ^ {b} \ cdot a ^ {c} = a ^ {b + c}}$ . Virasena, an Indian mathematician of the 8th century, studying power dependencies, published a table of integer indices (that is, in fact, logarithms) for bases 2, 3, 4 ^[28] .

The logarithmic table of M. Stifel, " Arithmetica integra ", 1544

The decisive step was taken in medieval Europe. The need for complex calculations in the 16th century grew rapidly, and a significant part of the difficulties was associated with the multiplication and division of multi-valued numbers, as well as the extraction of roots . At the end of the century, several mathematicians, almost simultaneously, came up with the idea: to replace the time-consuming multiplication by simple addition, using geometric tables to compare the geometric and arithmetic progressions, and the geometric one will be the original one ^[26] . Then the division is automatically replaced by an immeasurably simpler and more reliable subtraction, raising to a power and extracting the root will also be simplified.

The first to publish this idea in his book Arithmetica integra (1544) was Michael Stifel , who, however, did not make serious efforts to put his idea into practice ^[29] ^[30] . The main merit of Stifel is the transition from integer exponents to arbitrary rational ones ^[31] (the first steps in this direction were made by Nikolai Orem in the XIV century and Nikola Shyuk in the XV century).

John Napier and his “Amazing Logarithm Table”

John Napier

In 1614, the Scottish amateur mathematician John Napier published in Latin an essay entitled " Description of the amazing table of logarithms " ( lat. Mirifici Logarithmorum Canonis Descriptio ). It contained a brief description of the logarithms and their properties, as well as 8-digit tables of the logarithms of sines , cosines, and tangents , in increments of 1 '. The term logarithm , as proposed by Napier, has become firmly established in science. Nepher set forth the theory of logarithms in his other book, The Construction of the Amazing Logarithm Table ( lat. Mirifici Logarithmorum Canonis Constructio ), published posthumously in 1619 by his son Robert.

Judging by the documents, Nepher already owned the logarithm technique by 1594 ^[32] . The immediate goal of its development was to facilitate Napier complex astrological calculations ^[33] ; that is why only the logarithms of trigonometric functions were included in the tables.

There was no concept of a function then, and Naper defined the logarithm kinematically , comparing the uniform and logarithmic-slow motion; for example, he defined the logarithm of the sine as follows ^[34] :

The logarithm of a given sine is a number that always arithmetically increases at the same rate as the total sine began to decrease geometrically.

In modern notation, the kinematic model of Nepher can be represented by the differential equation ^[35] :

{\frac {dx}{x}}=-{\frac {dy}{M}}

{\ displaystyle {\ frac {dx} {x}} = - {\ frac {dy} {M}}}

,

where M is a scale factor introduced so that the value turns out to be an integer with the desired number of characters ( decimal fractions did not yet find wide application). Napier took M = 10,000,000.

Strictly speaking, Napier did not tabulate the function that is now called the logarithm. If we denote its function $\operatorname {LogNap} (x)$ ${\ displaystyle \ operatorname {LogNap} (x)}$ , then it is connected with the natural logarithm as follows ^[35] :

\operatorname {LogNap} (x)=M\cdot (\ln(M)-\ln(x))

{\ displaystyle \ operatorname {LogNap} (x) = M \ cdot (\ ln (M) - \ ln (x))}

Obviously $\operatorname {LogNap} (M)=0$ ${\ displaystyle \ operatorname {LogNap} (M) = 0}$ , that is, the logarithm of the "full sine" (corresponding to 90 °) is zero - this is what Neper achieved with his definition. He also wanted all logarithms to be positive; it is easy to verify that this condition for $x<M$ ${\ displaystyle x <M}$ performed. $\operatorname {LogNap} (0)=\infty$ ${\ displaystyle \ operatorname {LogNap} (0) = \ infty}$ .

The main property of the Napier logarithm: if the quantities form a geometric progression , then their logarithms form an arithmetic progression. However, the logarithm rules for the non-feather function were different from the rules for the modern logarithm, for example:

\operatorname {LogNap} (a\cdot b)=\operatorname {LogNap} (a)+\operatorname {LogNap} (b)-\operatorname {LogNap} (1)

{\ displaystyle \ operatorname {LogNap} (a \ cdot b) = \ operatorname {LogNap} (a) + \ operatorname {LogNap} (b) - \ operatorname {LogNap} (1)}

Further Development

As it was soon discovered, due to an error in the algorithm, all values of the Napier table contained incorrect numbers after the sixth digit ^[36] . However, this did not prevent the new calculation method from gaining widespread popularity, and many European mathematicians began to compile logarithmic tables. Kepler inserted an enthusiastic dedication to Napier in his 1620 astronomical reference book (not knowing that the inventor of logarithms had already passed away). In 1624, Kepler published his own version of the logarithmic tables ( lat. Chilias Logarithmorum ad totidem numeros rotundos ) ^[37] . The use of logarithms allowed Kepler to relatively quickly complete many years of work on the compilation of the Rudolfin tables , which cemented the success of heliocentric astronomy .

A few years after the book of Napier, logarithmic tables appeared, using a closer to modern understanding of the logarithm. London professor Henry Briggs published 14-digit tables of decimal logarithms (1617), and not for trigonometric functions, but for arbitrary integers to 1000 (7 years later, Briggs increased the number of numbers to 20,000). In 1619, John Speidell, a London math teacher, reprinted Napier's logarithmic tables, corrected and supplemented so that they actually became tables of natural logarithms. Spidell also had the logarithms of the numbers themselves up to 1000 (and the logarithm of the unit, like Brigs, was equal to zero) - although Spidell retained scaling to integers ^[38] ^[39] .

It soon became clear that the place of logarithms in mathematics is not limited to computational amenities. In 1629, the Belgian mathematician Gregoire de Saint-Vincent showed that the area under the hyperbole $y={\frac {1}{x}}$ ${\ displaystyle y = {\ frac {1} {x}}}$ changes according to the logarithmic law ^[40] . In 1668, the German mathematician Nicholas Mercator (Kaufman) discovered and published in his book Logarithmotechnia the expansion of the logarithm in an infinite series ^[41] . According to many historians, the appearance of logarithms had a strong influence on many mathematical concepts, including:

The formation and recognition of the general concept of irrational and transcendental numbers ^[42] .
The appearance of the exponential function and the general concept of a numerical function , the Euler number , the development of the theory of difference equations ^[43] .
Start of work with infinite rows ^[41] .
General methods for solving differential equations of various types.
Substantial development of the theory of numerical methods required to calculate exact logarithmic tables.

Until the end of the 19th century, there was no generally accepted logarithm designation, the base a was indicated either to the left or above the log symbol, then above it. In the end, the mathematicians came to the conclusion that the most convenient place for the base is below the line, after the log symbol: $\log _{a}b$ ${\ displaystyle \ log _ {a} b}$ . Brief designations of the most common types of logarithm - $\lg ,\;\ln$ ${\ displaystyle \ lg, \; \ ln}$ for decimal and natural, they appeared much earlier at once by several authors and finally became fixed by the end of the 19th century ^[44] .

A close-to-modern understanding of logarithm - as an operation opposite to exponentiation - first appeared in Wallis (1685) and Johann Bernoulli (1694), and was finally legalized by Euler ^[36] . In the book “Introduction to the Analysis of the Infinite” ( 1748 ) Euler gave modern definitions of both exponential and logarithmic functions, brought them into power series, and emphasized the role of the natural logarithm ^[45] . Euler also has the merit of extending the logarithmic function to the complex domain.

Extending the logarithm to a complex area

The first attempts to extend the logarithms to complex numbers were made at the turn of the 17th – 18th centuries by Leibniz and Johann Bernoulli , but they failed to create a holistic theory - primarily because the concept of the logarithm was not clearly defined then ^[46] . The discussion on this subject was first held between Leibniz and Bernoulli, and in the middle of the XVIII century - between D'Alembert and Euler. Bernoulli and D'Alembert believed that it should be determined $\log(-x)=\log(x)$ ${\ displaystyle \ log (-x) = \ log (x)}$ , while Leibniz argued that the logarithm of a negative number is an imaginary number ^[46] . The complete theory of the logarithms of negative and complex numbers was published by Euler in 1747-1751 and is essentially no different from the modern one ^[47] . Although the debate continued (D'Alembert defended his point of view and argued in detail in the article of his Encyclopedia and other works), Euler's approach to the end of the 18th century was universally recognized.

In the XIX century, with the development of complex analysis , the study of the complex logarithm stimulated new discoveries. Гаусс в 1811 году разработал полную теорию многозначности логарифмической функции ^[48] , определяемой как интеграл от ${\frac {1}{z}}$ ${\frac {1}{z}}$ . Риман , опираясь на уже известные факты об этой и аналогичных функциях, построил общую теорию римановых поверхностей .

Разработка теории конформных отображений показала, что меркаторская проекция в картографии , возникшая ещё до открытия логарифмов (1550), может быть описана как комплексный логарифм ^[49] .

Некоторые практические применения

Логарифмические зависимости в науке и природе

Логарифмические функции распространены чрезвычайно широко как в математике, так и в естественных науках. Часто логарифмы появляются там, где проявляется самоподобие , то есть некоторый объект последовательно воспроизводится в уменьшенном или увеличенном масштабе; см. ниже такие примеры, как рекурсивные алгоритмы , фракталы или раковины моллюсков. Приведём несколько примеров использования логарифмов в разнообразных науках.

Теория чисел

Распределение простых чисел асимптотически подчиняется простым законам ^[50] :

Число простых чисел в интервале от 1 до $n$ ${\ displaystyle n}$ приблизительно равно ${\frac {n}{\ln n}}$ ${\frac {n}{\ln n}}$ .
k -е простое число приблизительно равно $k\ln k$ $k\ln k$ .

Ещё более точные оценки используют интегральный логарифм .

Нередко возникает задача грубо оценить очень большое число — например, факториал или число Мерсенна с большим номером. Для этого было бы удобно приближённо записать число в экспоненциальном формате , то есть в виде мантиссы и десятичного порядка.

Задача легко решается с применением логарифмов. Рассмотрим для примера 44-е число Мерсенна $M=2^{32582657}-1$ $M=2^{32582657}-1$ .

\lg M\approx 32582657\cdot \lg 2\approx 9808357{,}09543

\lg M\approx 32582657\cdot \lg 2\approx 9808357{,}09543

Следовательно, мантисса результата равна $10^{0{,}09543}\approx 1{,}25.$ $10^{0{,}09543}\approx 1{,}25.$ Окончательно получим:

M\approx 1{,}25\cdot 10^{9808357}.

M\approx 1{,}25\cdot 10^{9808357}.

Математический анализ

Логарифмы нередко возникают при нахождении интегралов и при решении дифференциальных уравнений . Примеры:

\int {\operatorname {tg} x}\,dx=-\ln |\cos x|+C;\quad \int {\frac {dx}{\sqrt {x^{2}+a}}}=-\ln \ \left|\ x+{\sqrt {x^{2}+a}}\ \right|+C

\int {\operatorname {tg} x}\,dx=-\ln |\cos x|+C;\quad \int {\frac {dx}{\sqrt {x^{2}+a}}}=-\ln \ \left|\ x+{\sqrt {x^{2}+a}}\ \right|+C

Теория вероятностей и статистика

Распределение Бенфорда . По горизонтали — первые значащие цифры, по вертикали — вероятность их появления.

В статистике и теории вероятностей логарифм входит в ряд практически важных вероятностных распределений. Например, логарифмическое распределение ^[51] используется в генетике и физике. Логнормальное распределение часто встречается в ситуациях, когда исследуемая величина есть произведение нескольких независимых положительных случайных переменных ^[52] .

Закон Бенфорда («закон первой цифры») описывает вероятность появления определённой первой значащей цифры при измерении реальных величин.

Для оценки неизвестного параметра широко применяются метод максимального правдоподобия и связанная с ним логарифмическая функция правдоподобия ^[53] .

Флуктуации при случайном блуждании описывает закон Хинчина-Колмогорова .

Информатика и вычислительная математика

В информатике : единица измерения информации ( бит ). Например, для хранения в компьютере натурального числа $N$ ${\ displaystyle N}$ (в обычном для компьютера двоичном формате) понадобится $\log _{2}N+1$ $\log _{2}N+1$ битов.

Информационная энтропия — мера количества информации.

Оценка асимптотической сложности рекурсивных алгоритмов , основанных на принципе « разделяй и властвуй » ^[54] — таких как быстрая сортировка , быстрое преобразование Фурье и т. п.

Обычно числовые значения хранятся в памяти компьютера или специализированного процессора в формате с плавающей запятой . Если, однако, сложение и вычитание для группы данных выполняются редко, а умножение, деление, возведение в степень и извлечение корня — гораздо чаще, тогда имеет смысл рассмотреть возможность хранения таких данных в логарифмическом формате . В этом случае вместо числа хранится логарифм его модуля и знак , и скорость вычислений благодаря свойствам логарифма значительно повышается ^[55] . Логарифмический формат хранения был использован в нескольких системах, где доказал свою эффективность ^[56] ^[57] .

Фракталы и размерность

Треугольник Серпинского (справа)

Логарифмы помогают выразить размерность Хаусдорфа для фрактала ^[58] . Например, рассмотрим треугольник Серпинского , который получается из равностороннего треугольника последовательным удалением аналогичных треугольников, линейный размер каждого из которых на каждом этапе уменьшается вдвое (см. рисунок). Размерность результата определяется по формуле:

{\frac {\ln 3}{\ln 2}}\approx 1{,}58

{\frac {\ln 3}{\ln 2}}\approx 1{,}58

Механика и физика

Принцип Больцмана в статистической термодинамике — одна из важнейших функций состояния термодинамической системы , характеризующая степень её хаотичности .

Формула Циолковского применяется для расчёта скорости ракеты.

Химия и физическая химия

Уравнение Нернста связывает окислительно-восстановительный потенциал системы с активностями веществ, входящих в электрохимическое уравнение, а также со стандартными электродными потенциалами окислительно-восстановительных пар.

Логарифм используется в определениях таких величин, как показатель константы автопротолиза (самоионизации молекулы) и водородный показатель (кислотности раствора).

Теория музыки

Чтобы решить вопрос о том, на сколько частей делить октаву , требуется отыскать рациональное приближение для $\log _{2}{\frac {3}{2}}\approx 0{,}585$ $\log _{2}{\frac {3}{2}}\approx 0{,}585$ . Если разложить это число в непрерывную дробь , то третья подходящая дробь (7/12) позволяет обосновать классическое деление октавы на 12 полутонов ^[59] .

Психология и физиология

Человеческое восприятие многих явлений хорошо описывается логарифмическим законом.

Закон Вебера — Фехнера — эмпирический психофизиологический закон, заключающийся в том, что интенсивность ощущения пропорциональна логарифму интенсивности стимула ^[60] — громкости звука ^[61] , яркости света.

Закон Фиттса : чем дальше или точнее выполняется движение организма, тем больше коррекции необходимо для его выполнения и тем дольше эта коррекция исполняется ^[62] .

Время на принятие решения при наличии выбора можно оценить по ^[63] .

Biology

Ряд биологических форм хорошо соответствует логарифмической спирали ^[64] — кривой, у которой касательная в каждой точке образует с радиус-вектором в этой точке один и тот же угол, то есть прирост радиуса на единицу длины окружности постоянен:

Раковина наутилуса
Расположение семян на подсолнечнике
Цветная капуста Романеско

Miscellaneous

Число кругов игры по олимпийской системе равно двоичному логарифму от числа участников соревнований, округлённому до ближайшего большего целого ^[65] .

Логарифмическая шкала

Неравномерная шкала десятичных логарифмов используется во многих областях науки. Для обеспечения вычислений она наносится на логарифмические линейки . Другие примеры:

Акустика — уровень звукового давления и интенсивность звука ( децибелы ) ^[66] .
Отношение сигнал/шум в радиотехнике и электросвязи ^[67] .
Астрономия — шкала яркости звёзд ^[68] .
Химия — активность водородных ионов ( pH ) ^[69] .
Сейсмология — шкала Рихтера ^[70] .
Оптическая плотность — мера поглощения света прозрачными объектами или отражения света непрозрачными объектами ^[71] .
Фотографическая широта — характеристика светочувствительного материала ^[72] .
Шкала выдержек и диафрагм в фотографии ^[73] .
Теория музыки — нотная шкала, по отношению к частотам нотных звуков ^[59] .
Сельское хозяйство — основная гидрофизическая характеристика почвы ^[74] .
Теория управления — логарифмическая амплитудно-фазовая частотная характеристика ^[75] .

Логарифмическая шкала особенно удобна в тех случаях, когда уровни измеряемой величины образуют геометрическую прогрессию , поскольку тогда их логарифмы распределены с постоянным шагом. Например, 12 полутонов классической октавы образуют (приближённо) такую прогрессию ^[59] со знаменателем ${\sqrt[{12}]{2}}\approx 1{,}059$ ${\sqrt[{12}]{2}}\approx 1{,}059$ . Аналогично, каждый уровень шкалы Рихтера соответствует в 10 раз большей энергии, чем предыдущий уровень. Даже при отсутствии геометрической прогрессии логарифмическая шкала может пригодиться для компактного представления широкого диапазона значений измеряемой величины.

Логарифмическая шкала также широко применяется для оценки показателя степени в степенных зависимостях и коэффициента в показателе экспоненты. При этом график, построенный в логарифмическом масштабе по одной или двум осям, принимает вид прямой, более простой для исследования.

Графики трёх функций при различном выборе шкал по осям координат:
Верхний ряд - 1) обе линейные; 2) логарифмическая (x) и линейная (y);
Нижний ряд - 1) линейная (x) и логарифмическая (y); 2) обе логарифмические.

y=10^{x}

y=10^{x}

y=x

{\displaystyle y=x}

y=\ln x

y=\ln x

Логарифмические таблицы

Из свойств логарифма следует, что вместо трудоёмкого умножения многозначных чисел достаточно найти (по таблицам) и сложить их логарифмы, а потом по тем же таблицам (раздел « Антилогарифмы ») выполнить потенцирование , то есть найти значение результата по его логарифму. Выполнение деления отличается только тем, что логарифмы вычитаются.

Первые таблицы логарифмов опубликовал Джон Непер ( 1614 ), и они содержали только логарифмы тригонометрических функций , причём с ошибками. Независимо от него свои таблицы опубликовал Йост Бюрги , друг Кеплера ( 1620 ). В 1617 году оксфордский профессор математики Генри Бригс опубликовал таблицы, которые уже включали десятичные логарифмы самих чисел, от 1 до 1000, с 8 (позже — с 14) знаками. Но и в таблицах Бригса обнаружились ошибки. Первое безошибочное издание на основе таблиц Георга Веги ( 1783 ) появилось только в 1857 году в Берлине (таблицы Бремикера, Carl Bremiker ) ^[76] .

В России первые таблицы логарифмов были изданы в 1703 году при участии Л. Ф. Магницкого ^[77] . В СССР выпускались несколько сборников таблиц логарифмов ^[78] :

Брадис В. М. Четырёхзначные математические таблицы. М.: Дрофа, 2010, ISBN 978-5-358-07433-0 . Таблицы Брадиса, издаваемые с 1921 года, использовались в учебных заведениях и в инженерных расчётах, не требующих большой точности. Они содержали мантиссы десятичных логарифмов чисел и тригонометрических функций, натуральные логарифмы и некоторые другие полезные расчётные инструменты.
Вега Г. Таблицы семизначных логарифмов, 4-е издание, М.: Недра, 1971. Профессиональный сборник для точных вычислений.
Бремикер К. Логарифмо-тригонометрические таблицы. М.: Наука, 1962. 664 с. Классические шестизначные таблицы, удобные для расчётов с тригонометрическими функциями .
Пятизначные таблицы натуральных значений тригонометрических величин, их логарифмов и логарифмов чисел, 6-е издание, М.: Наука, 1972.
Таблицы натуральных логарифмов, 2-е издание, в 2 томах, М.: Наука, 1971.
Десятизначные таблицы логарифмов комплексных чисел. М., 1952.

Логарифмическая линейка

В 1620-е годы Эдмунд Уингейт и Уильям Отред изобрели первую логарифмическую линейку , до появления карманных калькуляторов служившую незаменимым расчётным орудием инженера ^[79] . С помощью этого компактного инструмента можно быстро производить все алгебраические операции, в том числе с участием тригонометрических функций ^[80] . Точность расчётов — около 3 значащих цифр.

Логарифмическая линейка. Умножение 1,3 × 2 или деление 2,6 / 2 (см. шкалы C и D).

Вариации и обобщения

Логарифм как решение уравнения $a^{x}=b$ $a^{x}=b$ можно определить не только для вещественных и комплексных чисел.

Можно ввести логарифмическую функцию для кватернионов (см. функции кватернионного переменного ). Однако большинство алгебраических свойств логарифма при этом теряется ^[81] — например, логарифм произведения не равен сумме логарифмов, и это снижает практическую ценность такого обобщения.
If a $a, b$ ${\displaystyle a,b}$ — элементы конечной абелевой мультипликативной группы , то логарифм в указанном смысле (если он существует) называется дискретным . Чаще всего он рассматривается для конечной группы кольца вычетов по некоторому модулю, где называется индексом по этому модулю ^[82] и играет важную роль в криптографии . В циклических группах логарифм существует, если его основание является первообразным корнем этой группы.
: можно определить логарифмы также для матриц ^[83] .
Можно определить для некоторых p-адических чисел ^[84] .
Для работы с очень большими числами вводится понятие суперлогарифма , связанное не с возведением в степень , а с операцией более высокого порядка: тетрацией .

Notes

↑ Краткий словарь иностранных слов. М.: Русский язык, 1984.
↑ Выгодский М. Я. Справочник по элементарной математике, 1978 , с. 186.
↑ Выгодский М. Я. Справочник по элементарной математике, 1978 , с. 184-186.
↑ Швецов К. И., Бевз Г. П. Справочник по элементарной математике. Арифметика, алгебра. Киев: Наукова Думка, 1966. §40. Исторические сведения о логарифмах и логарифмической линейке.
↑ ¹ ² Корн Г., Корн Т. Справочник по математике, 1973 , с. 34.
↑ Алгебра и начала анализа. Учебник для 10-11 классов. 12-е издание, М.: Просвещение, 2002. Стр. 229.
↑ Алгебра и начала анализа. Учебник для 10-11 классов. 12-е издание, М.: Просвещение, 2002. Стр. 233.
↑ Выгодский М. Я. Справочник по элементарной математике, 1978 , с. 187.
↑ Элементарная математика, 1976 , с. 93f.
↑ ¹ ² Элементарная математика, 1976 , с. 89.
↑ ¹ ² Логарифмическая функция. // Математическая энциклопедия (в 5 томах) . — М. : Советская Энциклопедия , 1982. — Т. 3.
↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966 , Том I, стр. 159-160.
↑ Sasaki T., Kanada Y. Practically fast multiple-precision evaluation of log(x) (англ.) // Journal of Information Processing. — 1982. — Vol. 5 , iss. 4 . — P. 247—250 .
↑ ¹ ² Элементарная математика, 1976 , с. 94—100.
↑ Выгодский М. Я. Справочник по элементарной математике, 1978 , с. 189.
↑ Клейн Ф. Элементарная математика с точки зрения высшей, 1987 , с. 406.
↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966 , Том I, стр. 164.
↑ Baker, Alan (1975), Transcendental number theory , Cambridge University Press, ISBN 978-0-521-20461-3 , p. ten.
↑ ¹ ² Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966 , Том II, стр. 520-522.
↑ ¹ ² Корн Г., Корн Т. Справочник по математике, 1973 , с. 623.
↑ Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной, 1967 , с. 92-94.
↑ ¹ ² ³ Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной, 1967 , с. 45-46, 99-100.
↑ Болтянский В. Г. , Ефремович В. А. Наглядная топология . — М. : Наука, 1982. — С. 112. — (Библиотечка Квант, выпуск 21).
↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966 , Том II, стр. 522-526.
↑ ¹ ² Корн Г., Корн Т. Справочник по математике, 1973 , с. 624.
↑ ¹ ² Успенский Я. В. Очерк истории логарифмов, 1923 , с. 9.
↑ Клейн Ф. Элементарная математика с точки зрения высшей, 1987 , с. 206.
↑ Gupta, RC (2000), "History of Mathematics in India" , in Hoiberg, Dale & Ramchandani, Students' Britannica India: Select essays , New Delhi: Popular Prakashan, с. 329
↑ История математики, том II, 1970 , с. 54-55.
↑ Vivian Shaw Groza, Susanne M. Shelley (1972), Precalculus mathematics , New York: Holt, Rinehart, Winston, с. 182, ISBN 978-0-03-077670-0 , < https://books.google.com/?id=yM_lSq1eJv8C&pg=PA182&dq=%22arithmetica+integra%22+logarithm&q=stifel >
↑ Клейн Ф. Элементарная математика с точки зрения высшей, 1987 , с. 210.
↑ Успенский Я. В. Очерк истории логарифмов, 1923 , с. 13.
↑ История математики, том II, 1970 , с. 56.
↑ Хрестоматия по истории математики. Математический анализ. Теория вероятностей / Под ред. А. П. Юшкевича . — М. : Просвещение, 1977. — С. 40. — 224 с.
↑ ¹ ² История математики, том II, 1970 , с. 59.
↑ ¹ ² История математики, том II, 1970 , с. 61.
↑ Успенский Я. В. Очерк истории логарифмов, 1923 , с. 39.
↑ История математики, том II, 1970 , с. 63.
↑ Charles Hutton. Mathematical Tables. London, 1811, p. thirty.
↑ История математики, том II, 1970 , с. 133.
↑ ¹ ² Успенский Я. В. Очерк истории логарифмов, 1923 , с. 52.
↑ Клейн Ф. Элементарная математика с точки зрения высшей, 1987 , с. 51, 286, 352.
↑ Клейн Ф. Элементарная математика с точки зрения высшей, 1987 , с. 213, 217.
↑ Cajori., Florian. A History of Mathematics, 5th ed . — AMS Bookstore, 1991. — P. 152. — ISBN 0821821024 .
↑ Рыбников К. А. История математики. В двух томах. — М. : Изд. МГУ, 1963. — Т. II. — С. 25.
↑ ¹ ² История математики, том III, 1972 , с. 325-328.
↑ Рыбников К. А. История математики. В двух томах. — М. : Изд. МГУ, 1963. — Т. II. — С. 27, 230-231.
↑ Математика XIX века. Том II: Геометрия. Теория аналитических функций, 1981 , с. 122-123.
↑ Клейн Ф. Элементарная математика с точки зрения высшей . — М. : Наука, 1987. — Т. II. Geometry. — С. 159-161. - 416 p.
↑ Дербишир, Джон. Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике. — Астрель, 2010. — 464 с. — ISBN 978-5-271-25422-2 .
↑ Weisstein, Eric W. Log-Series Distribution (англ.) . MathWorld. Дата обращения 26 апреля 2012.
↑ Логарифмически нормальное распределение // Математическая энциклопедия (в 5 томах) . — М. : Советская Энциклопедия , 1982. — Т. 3.
↑ Максимального правдоподобия метод // Математическая энциклопедия (в 5 томах) . — М. : Советская Энциклопедия , 1982. — Т. 3.
↑ Harel, David; Feldman, Yishai A. Algorithmics: the spirit of computing. — New York: Addison-Wesley, 2004. — P. 143. — ISBN 978-0-321-11784-7 .
↑ NG Kingsburg, PJW Rayner. Digital filtering using logarithmic arithmetic (англ.) // Electronics Letters : journal. — 1971. — 28 January ( vol. 7 ). — P. 55 .
↑ RC Ismail and JN Coleman. ROM-less LNS (неопр.) // 2011 20th IEEE Symposium on Computer Arithmetic (ARITH). — 2011. — July. — С. 43—51 . — DOI : 10.1109/ARITH.2011.15 .
↑ Haohuan Fu, Oskar Mencer, Wayne Luk. Comparing Floating-point and Logarithmic Number Representations for Reconfigurable Acceleration (англ.) // IEEE Conference on Field Programmable Technology : journal. — 2006. — December. — P. 337 . — DOI : 10.1109/FPT.2006.270342 .
↑ Иванов М. Г. Размер и размерность // «Потенциал», август 2006.
↑ ¹ ² ³ Шилов Г. Е. Простая гамма. Устройство музыкальной шкалы. М.: Физматгиз, 1963. 20 с. Серия «Популярные лекции по математике», выпуск 37.
↑ Головин С. Ю. ЗАКОН ВЕБЕРА-ФЕХНЕРА // Словарь практического психолога (неопр.) . Дата обращения 17 апреля 2012. Архивировано 28 мая 2012 года.
↑ Irina Aldoshina. Fundamentals of psychoacoustics // Sound producer. - 1999. - Vol. 6 .
↑ Fitts Law // Psychological Encyclopedia (Neopr.) . Date of treatment April 17, 2012. Archived on May 28, 2012.
↑ Welford, AT Fundamentals of skill. - London: Methuen, 1968. - P. 61. - ISBN 978-0-416-03000-6 .
↑ Logarithmic spiral // Mathematical Encyclopedic Dictionary / Ch. ed. Yu. V. Prokhorov . - M .: Soviet Encyclopedia , 1988 .-- S. 328. - 847 p. - ISBN 5-85270-278-1 .
↑ Harin A.A. Organization and holding of competitions. Methodical manual . - Izhevsk: Udmurt State University, 2011 .-- S. 27.
↑ Decibel // Great Soviet Encyclopedia : [in 30 vol.] / Ch. ed. A.M. Prokhorov . - 3rd ed. - M .: Soviet Encyclopedia, 1969-1978.
↑ Educational-methodical complex: Methods and means of signal processing (neopr.) . Date of treatment April 28, 2012. Archived February 19, 2012.
↑ Magnitude // Great Soviet Encyclopedia : [in 30 vol.] / Ch. ed. A.M. Prokhorov . - 3rd ed. - M .: Soviet Encyclopedia, 1969-1978.
↑ R. Bates. Determination of pH. Theory and practice. - 2 ed. - L .: Chemistry, 1972.
↑ Richter scale (neopr.) . Geography. Modern illustrated encyclopedia. - M.: Rosman. Edited by prof. A.P. Gorkin. 2006. Archived on August 23, 2011.
↑ Optical density // Photokinotechnics: Encyclopedia / Ch. ed. E.A. Iophis . - M .: Soviet Encyclopedia , 1981.- 447 p.
↑ Photographic latitude // Photokinotechnics: Encyclopedia / Ch. ed. E.A. Iophis . - M .: Soviet Encyclopedia , 1981.- 447 p.
↑ Kulagin S.V. Excerpt // Photokinotechnics: Encyclopedia / Ch. ed. E.A. Iophis . - M .: Soviet Encyclopedia , 1981.- 447 p.
↑ Shein E.V. Course in soil physics. M .: Publishing house of Moscow State University, 2005 .-- 432 p. ISBN 5-211-05021-5 .
↑ The concept of frequency characteristics (neopr.) . Date of treatment April 28, 2012. Archived May 28, 2012.
↑ History of Mathematics, Volume II, 1970 , p. 62.
↑ Gnedenko B.V. Essays on the History of Mathematics in Russia, 2nd edition. - M .: KomKniga, 2005 .-- S. 66. - 296 p. - ISBN 5-484-00123-4 .
↑ Logarithmic tables // Great Soviet Encyclopedia .
↑ History of Mathematics, Volume II, 1970 , p. 65-66.
↑ Berezin S.I. Countable slide rule. - M .: Mechanical Engineering, 1968.
↑ David Eberly. Quaternion algebra and calculus (English) (March 2, 1999). Date of treatment April 12, 2012. Archived May 28, 2012.
↑ Vinogradov I. M. Fundamentals of number theory . - M.-L.: GITTL, 1952. - S. 97. - 180 p.
↑ Gantmakher F.R. Matrix Theory. - M .: Nauka, 1967 .-- 576 p.
↑ p-adic exponential and p-adic logarithm (Eng.) // PlanetMath.org.

Literature

Theory of Logarithms

Vygodsky M. Ya. Handbook of Elementary Mathematics . - M .: Science, 1978.
- Reprint: AST, 2003, ISBN 5-17-009554-6 .
Zaitsev V.V., Ryzhkov V.V., Skanavi M.I. Elementary mathematics. Repeat course. - Third edition, stereotyped. - M .: Nauka, 1976 .-- 591 p.
Korn G., Korn T. Handbook of mathematics (for scientists and engineers) . - M .: Nauka, 1973.- 720 p.
Sveshnikov A.G., Tikhonov A.N. Theory of functions of a complex variable. - M .: Nauka, 1967 .-- 304 p.
Fichtenholtz G. M. The course of differential and integral calculus. - ed. 6th - M .: Nauka, 1966 .-- 680 p.
Chessmaster A. Kh. Logarithms. A manual for students, applicants and teachers. - ed. 5th. - SPb. : MCCMO, 2016 .-- 288 p. - ISBN 978-5-4439-0648-5 .

Logarithm History

Abelson I. B. Birth of logarithms . - M. — L .: Gostekhizdat, 1948 .-- 231 p.
Hirschwald L. Ya. History of the discovery of logarithms. - Kharkov: Kharkov University Press, 1952. - 33 p.
Klein F. Elementary mathematics from the point of view of higher . - M .: Nauka, 1987. - T. I. Arithmetic. Algebra. Analysis. - 432 s.
Mathematics of the XVII century // History of mathematics / Edited by A.P. Yushkevich , in three volumes. - M .: Nauka, 1970 .-- T. II.
Mathematics of the XVIII century // History of Mathematics / Edited by A.P. Yushkevich , in three volumes. - M .: Nauka, 1972 .-- T. III.
Kolmogorov A.N., Yushkevich A.P. (Ed.). Mathematics of the XIX century. Geometry. Theory of analytic functions. - M .: Nauka, 1981. - T. II.
Uspensky Y. V. Sketch of the history of logarithms. - Petrograd: Scientific publishing house, 1923. - 78 p.

[1] Краткий словарь иностранных слов. М.: Русский язык, 1984.

[_1199262b77eb0e07-2] Выгодский М. Я. Справочник по элементарной математике, 1978 , с. 186.

[_e424803642e14d91-3] Выгодский М. Я. Справочник по элементарной математике, 1978 , с. 184-186.

[4] Швецов К. И., Бевз Г. П. Справочник по элементарной математике. Арифметика, алгебра. Киев: Наукова Думка, 1966. §40. Исторические сведения о логарифмах и логарифмической линейке.

[KORN34-5] ¹ ² Корн Г., Корн Т. Справочник по математике, 1973 , с. 34.

[6] Алгебра и начала анализа. Учебник для 10-11 классов. 12-е издание, М.: Просвещение, 2002. Стр. 229.

[7] Алгебра и начала анализа. Учебник для 10-11 классов. 12-е издание, М.: Просвещение, 2002. Стр. 233.

[_1199262b77eb0e06-8] Выгодский М. Я. Справочник по элементарной математике, 1978 , с. 187.

[_01e0f0deb88b94fb-9] Элементарная математика, 1976 , с. 93f.

[ZAY89-10] ¹ ² Элементарная математика, 1976 , с. 89.

[MATENC-11] ¹ ² Логарифмическая функция. // Математическая энциклопедия (в 5 томах) . — М. : Советская Энциклопедия , 1982. — Т. 3.

[_61b5b0996750f73d-12] Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966 , Том I, стр. 159-160.

[13] Sasaki T., Kanada Y. Practically fast multiple-precision evaluation of log(x) (англ.) // Journal of Information Processing. — 1982. — Vol. 5 , iss. 4 . — P. 247—250 .

[ZAY94-14] ¹ ² Элементарная математика, 1976 , с. 94—100.

[_1199262b77eb0e08-15] Выгодский М. Я. Справочник по элементарной математике, 1978 , с. 189.

[_e338002fcb6b068b-16] Клейн Ф. Элементарная математика с точки зрения высшей, 1987 , с. 406.

[_d7c980ebfc5ca395-17] Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966 , Том I, стр. 164.

[18] Baker, Alan (1975), Transcendental number theory , Cambridge University Press, ISBN 978-0-521-20461-3 , p. ten.

[FICHT2-520-19] ¹ ² Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966 , Том II, стр. 520-522.

[KORN623-20] ¹ ² Корн Г., Корн Т. Справочник по математике, 1973 , с. 623.

[_67bc3b70f18c5d99-21] Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной, 1967 , с. 92-94.

[ST-22] ¹ ² ³ Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной, 1967 , с. 45-46, 99-100.

[23] Болтянский В. Г. , Ефремович В. А. Наглядная топология . — М. : Наука, 1982. — С. 112. — (Библиотечка Квант, выпуск 21).

[FICHT2-522-24] Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966 , Том II, стр. 522-526.

[KK624-25] ¹ ² Корн Г., Корн Т. Справочник по математике, 1973 , с. 624.

[USP9-26] ¹ ² Успенский Я. В. Очерк истории логарифмов, 1923 , с. 9.

[_e331742fcb65ad1d-27] Клейн Ф. Элементарная математика с точки зрения высшей, 1987 , с. 206.

[28] Gupta, RC (2000), "History of Mathematics in India" , in Hoiberg, Dale & Ramchandani, Students' Britannica India: Select essays , New Delhi: Popular Prakashan, с. 329

[_28c9986ff3d6debc-29] История математики, том II, 1970 , с. 54-55.

[30] Vivian Shaw Groza, Susanne M. Shelley (1972), Precalculus mathematics , New York: Holt, Rinehart, Winston, с. 182, ISBN 978-0-03-077670-0 , < https://books.google.com/?id=yM_lSq1eJv8C&pg=PA182&dq=%22arithmetica+integra%22+logarithm&q=stifel >

[_e331732fcb65ab48-31] Клейн Ф. Элементарная математика с точки зрения высшей, 1987 , с. 210.

[USP13-32] Успенский Я. В. Очерк истории логарифмов, 1923 , с. 13.

[_aaec9a6abc5f1b17-33] История математики, том II, 1970 , с. 56.

[34] Хрестоматия по истории математики. Математический анализ. Теория вероятностей / Под ред. А. П. Юшкевича . — М. : Просвещение, 1977. — С. 40. — 224 с.

[HIST59-35] ¹ ² История математики, том II, 1970 , с. 59.

[IM61-36] ¹ ² История математики, том II, 1970 , с. 61.

[_1a1eee2c713fef4a-37] Успенский Я. В. Очерк истории логарифмов, 1923 , с. 39.

[_aaec976abc5f163b-38] История математики, том II, 1970 , с. 63.

[39] Charles Hutton. Mathematical Tables. London, 1811, p. thirty.

[_cf330d5e15a68c09-40] История математики, том II, 1970 , с. 133.

[USP52-41] ¹ ² Успенский Я. В. Очерк истории логарифмов, 1923 , с. 52.

[_a4af7f26ec01fc6b-42] Клейн Ф. Элементарная математика с точки зрения высшей, 1987 , с. 51, 286, 352.

[_44b1045f1dc070fb-43] Клейн Ф. Элементарная математика с точки зрения высшей, 1987 , с. 213, 217.

[44] Cajori., Florian. A History of Mathematics, 5th ed . — AMS Bookstore, 1991. — P. 152. — ISBN 0821821024 .

[45] Рыбников К. А. История математики. В двух томах. — М. : Изд. МГУ, 1963. — Т. II. — С. 25.

[IM3-325-46] ¹ ² История математики, том III, 1972 , с. 325-328.

[47] Рыбников К. А. История математики. В двух томах. — М. : Изд. МГУ, 1963. — Т. II. — С. 27, 230-231.

[_336cb09363c90cbe-48] Математика XIX века. Том II: Геометрия. Теория аналитических функций, 1981 , с. 122-123.

[49] Клейн Ф. Элементарная математика с точки зрения высшей . — М. : Наука, 1987. — Т. II. Geometry. — С. 159-161. - 416 p.

[50] Дербишир, Джон. Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике. — Астрель, 2010. — 464 с. — ISBN 978-5-271-25422-2 .

[51] Weisstein, Eric W. Log-Series Distribution (англ.) . MathWorld. Дата обращения 26 апреля 2012.

[52] Логарифмически нормальное распределение // Математическая энциклопедия (в 5 томах) . — М. : Советская Энциклопедия , 1982. — Т. 3.

[53] Максимального правдоподобия метод // Математическая энциклопедия (в 5 томах) . — М. : Советская Энциклопедия , 1982. — Т. 3.

[54] Harel, David; Feldman, Yishai A. Algorithmics: the spirit of computing. — New York: Addison-Wesley, 2004. — P. 143. — ISBN 978-0-321-11784-7 .

[55] NG Kingsburg, PJW Rayner. Digital filtering using logarithmic arithmetic (англ.) // Electronics Letters : journal. — 1971. — 28 January ( vol. 7 ). — P. 55 .

[56] RC Ismail and JN Coleman. ROM-less LNS (неопр.) // 2011 20th IEEE Symposium on Computer Arithmetic (ARITH). — 2011. — July. — С. 43—51 . — DOI : 10.1109/ARITH.2011.15 .

[57] Haohuan Fu, Oskar Mencer, Wayne Luk. Comparing Floating-point and Logarithmic Number Representations for Reconfigurable Acceleration (англ.) // IEEE Conference on Field Programmable Technology : journal. — 2006. — December. — P. 337 . — DOI : 10.1109/FPT.2006.270342 .

[58] Иванов М. Г. Размер и размерность // «Потенциал», август 2006.

[Shilov-59] ¹ ² ³ Шилов Г. Е. Простая гамма. Устройство музыкальной шкалы. М.: Физматгиз, 1963. 20 с. Серия «Популярные лекции по математике», выпуск 37.

[60] Головин С. Ю. ЗАКОН ВЕБЕРА-ФЕХНЕРА // Словарь практического психолога (неопр.) . Дата обращения 17 апреля 2012. Архивировано 28 мая 2012 года.

[61] Irina Aldoshina. Fundamentals of psychoacoustics // Sound producer. - 1999. - Vol. 6 .

[62] Fitts Law // Psychological Encyclopedia (Neopr.) . Date of treatment April 17, 2012. Archived on May 28, 2012.

[63] Welford, AT Fundamentals of skill. - London: Methuen, 1968. - P. 61. - ISBN 978-0-416-03000-6 .

[64] Logarithmic spiral // Mathematical Encyclopedic Dictionary / Ch. ed. Yu. V. Prokhorov . - M .: Soviet Encyclopedia , 1988 .-- S. 328. - 847 p. - ISBN 5-85270-278-1 .

[65] Harin A.A. Organization and holding of competitions. Methodical manual . - Izhevsk: Udmurt State University, 2011 .-- S. 27.

[66] Decibel // Great Soviet Encyclopedia : [in 30 vol.] / Ch. ed. A.M. Prokhorov . - 3rd ed. - M .: Soviet Encyclopedia, 1969-1978.

[67] Educational-methodical complex: Methods and means of signal processing (neopr.) . Date of treatment April 28, 2012. Archived February 19, 2012.

[68] Magnitude // Great Soviet Encyclopedia : [in 30 vol.] / Ch. ed. A.M. Prokhorov . - 3rd ed. - M .: Soviet Encyclopedia, 1969-1978.

[69] R. Bates. Determination of pH. Theory and practice. - 2 ed. - L .: Chemistry, 1972.

[70] Richter scale (neopr.) . Geography. Modern illustrated encyclopedia. - M.: Rosman. Edited by prof. A.P. Gorkin. 2006. Archived on August 23, 2011.

[71] Optical density // Photokinotechnics: Encyclopedia / Ch. ed. E.A. Iophis . - M .: Soviet Encyclopedia , 1981.- 447 p.

[72] Photographic latitude // Photokinotechnics: Encyclopedia / Ch. ed. E.A. Iophis . - M .: Soviet Encyclopedia , 1981.- 447 p.

[73] Kulagin S.V. Excerpt // Photokinotechnics: Encyclopedia / Ch. ed. E.A. Iophis . - M .: Soviet Encyclopedia , 1981.- 447 p.

[74] Shein E.V. Course in soil physics. M .: Publishing house of Moscow State University, 2005 .-- 432 p. ISBN 5-211-05021-5 .

[75] The concept of frequency characteristics (neopr.) . Date of treatment April 28, 2012. Archived May 28, 2012.

[_aaec976abc5f163a-76] History of Mathematics, Volume II, 1970 , p. 62.

[77] Gnedenko B.V. Essays on the History of Mathematics in Russia, 2nd edition. - M .: KomKniga, 2005 .-- S. 66. - 296 p. - ISBN 5-484-00123-4 .

[78] Logarithmic tables // Great Soviet Encyclopedia .

[_7c180c58304b496e-79] History of Mathematics, Volume II, 1970 , p. 65-66.

[80] Berezin S.I. Countable slide rule. - M .: Mechanical Engineering, 1968.

[81] David Eberly. Quaternion algebra and calculus (English) (March 2, 1999). Date of treatment April 12, 2012. Archived May 28, 2012.

[82] Vinogradov I. M. Fundamentals of number theory . - M.-L.: GITTL, 1952. - S. 97. - 180 p.

[83] Gantmakher F.R. Matrix Theory. - M .: Nauka, 1967 .-- 576 p.

[84] -adic exponential and p-adic logarithm (Eng.) // PlanetMath.org.